23.2. Графік зведеного динамічного моменту інерції механізму.

Побудуємо графік зведеного динамічного моменту інерції механізму за цикл І_зв = І_зв(φ) рис.23.1,г/.

Числові значення зведеного динамічного моменту інерції для кож­ного механізму визначаються із формули, яка виводиться із умови рів­ності кінетичних енергій /див. лекція 21, питання 4/.

Визначимо масштаб графіка зведеного динамічного моменту інерції:

/23.7/

де І_зві - зведений динамічний момент інерції механізму в і-му положен­ні; X_i - відрізок в мм на рис.23.1,г, що зображає цей момент І_зві.

Графіки для визначення динамічного моменту інерції маховика

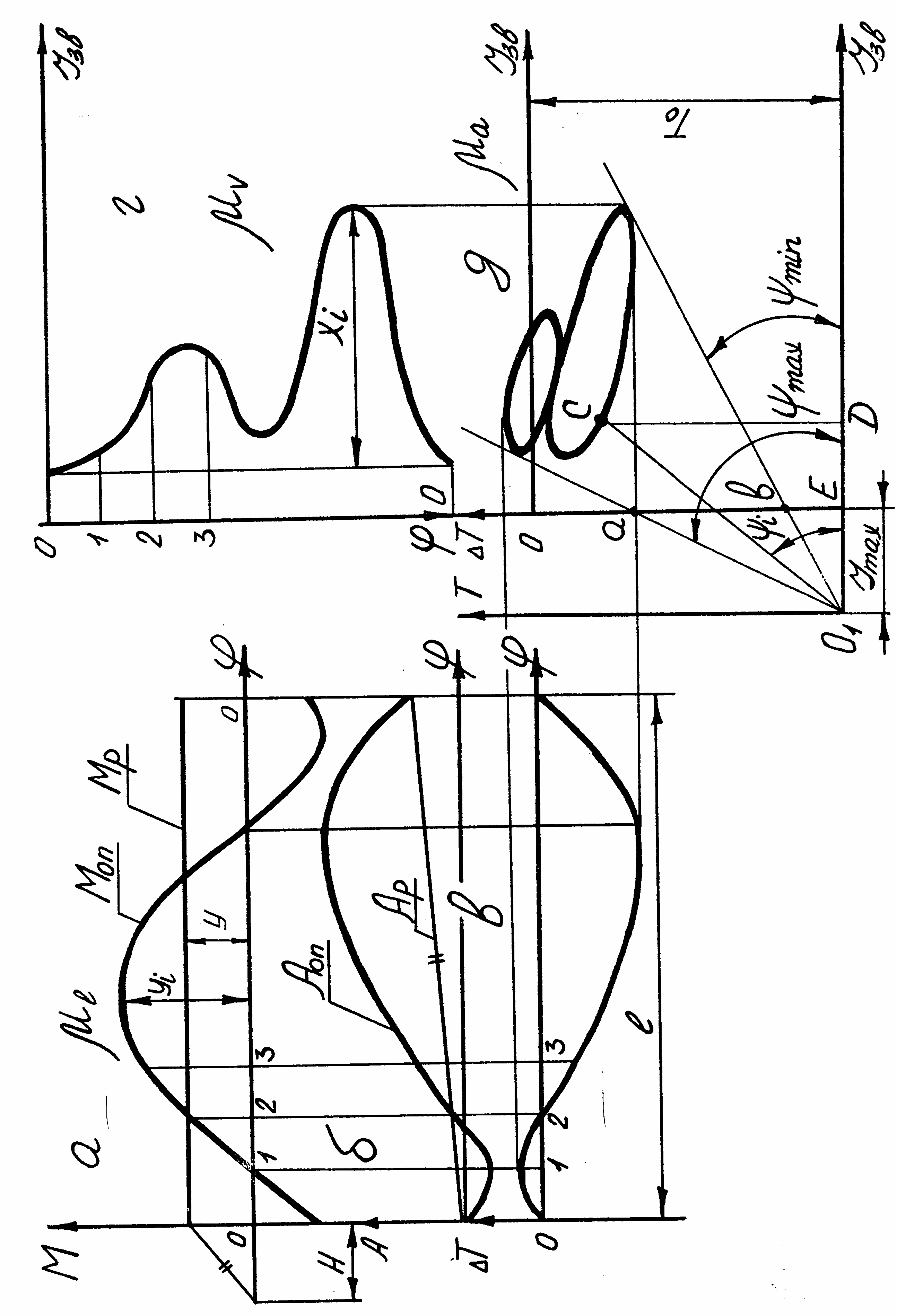
Рис.23.1

23.3. Діаграма енергомас.

Побудуємо діаграму енергомас /рис.23.1,д/. Цю діаграму будуємо графічним складанням графіків приросту кінетичної енергії механізму /рис.23.1,в/ і зведеного динамічного моменту інер­ції механізму І_зв = І_зв(φ) рис.23.1,г/ методом виключення параметру φ .

Проведемо дотичні до діаграми енергомас під кутами ψ_max і ψ_min /рис.23.1,д/. Отримаємо на перетині цих дотичних з віссю відрізок, який позначимо .

Визначимо кути ψ_max і ψ_min .Точка 0₁- перетину дотичних буде по­чатком нових осей координат діаграми повної кінетичної енергії всьо­го механізму у функції повного зведеного динамічного моменту інерції механізму з маховиком.

Для будь-якої точки С діаграми енергомас можна записати:

О₁Д = ЕД + О₁Е, /23.8/

де О₁Д - відрізок, що зображає повний зведений динамічний момент інерції механізму з маховиком; ЕД - відрізок, що зображає зведений динамічний момент інерції механізму; О₁Е - відрізок, що зображає мо­мент інерції маховика.

Із трикутника О₁СД маємо:

/23.9/

Визначимо кутову швидкість вхідної ланки в будь-якому і-му поло­женні механізму. Із рівняння кінетичної енергії маємо:

/23.10/

де Т_і = СД * μ _, І_зві = О₁Дμ_Ізв.

Підставимо значення Т_і і І_зві в рівняння /23.10/, отримаємо:

/23.11/

Враховуючи відношення /23.9/, знайдемо:

/23.12/

Підставимо в рівняння /23.12/ значення ω_max і ω_min із /22.13/ і /22.14/. Знайдемо ψ_max i ψ_min. Зважаючи на малу величину коефіцієн­та δ, членом нехтуємо. Тоді отримаємо:

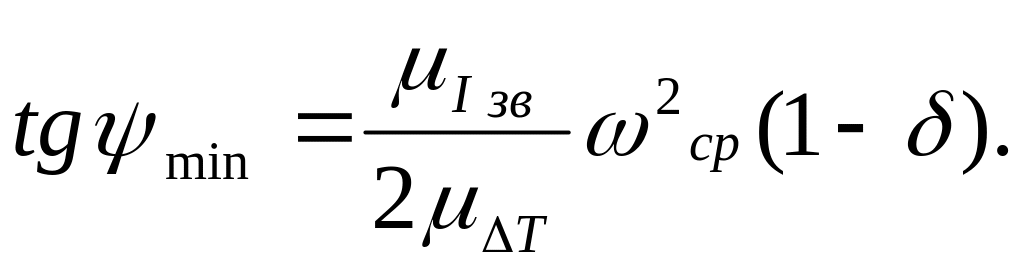/23.13/

23.4. Динамічний момент інерції та геометричні розміри маховика. Визначимо динамічний момент інерції маховика I_maх. із рис.23.1,д:

I_max = O₁E * μ_Iзв /23.14/

Таким чином, вимірюючи в міліметрах безпосередньо із рис.23.1,д від­різок 0₁Е за формулою /23.14/ визначимо динамічний момент інерції маховика. Проте при малому значенні коефіцієнта нерівномірності δ точка перетину О₁ дотичних може вийти за межі рисунка. Значно прос­тіше користуватися відрізком ав. Із рисунка видно, що:

aE = O₁Etgψ_max i bE = O₁Etgψ_min.

Віднімемо від першого рівняння друге, отримаємо:

aE – bE = O₁E(tgψ_max – tgψ_min). /23.15/

Із відношення /23.15/ знаходимо:

/23.16/

Підставимо значення ψ_max і ψ_min. із /23.13/ і 0_ІЕ із /23.14/ в формулу /23.16/, отримаємо:

/23.17/

Звідки знаходимо:

/23.18/

Визначимо геометричні розміри маховика.

Вважаємо, що маса маховика рівномірно розподілена по колу діамет­ра D, а також нехтуємо моментами інерції маточини і спиць, оскільки вони відносно невеликі /рис.23.2/. Момент інерції можна подати так:

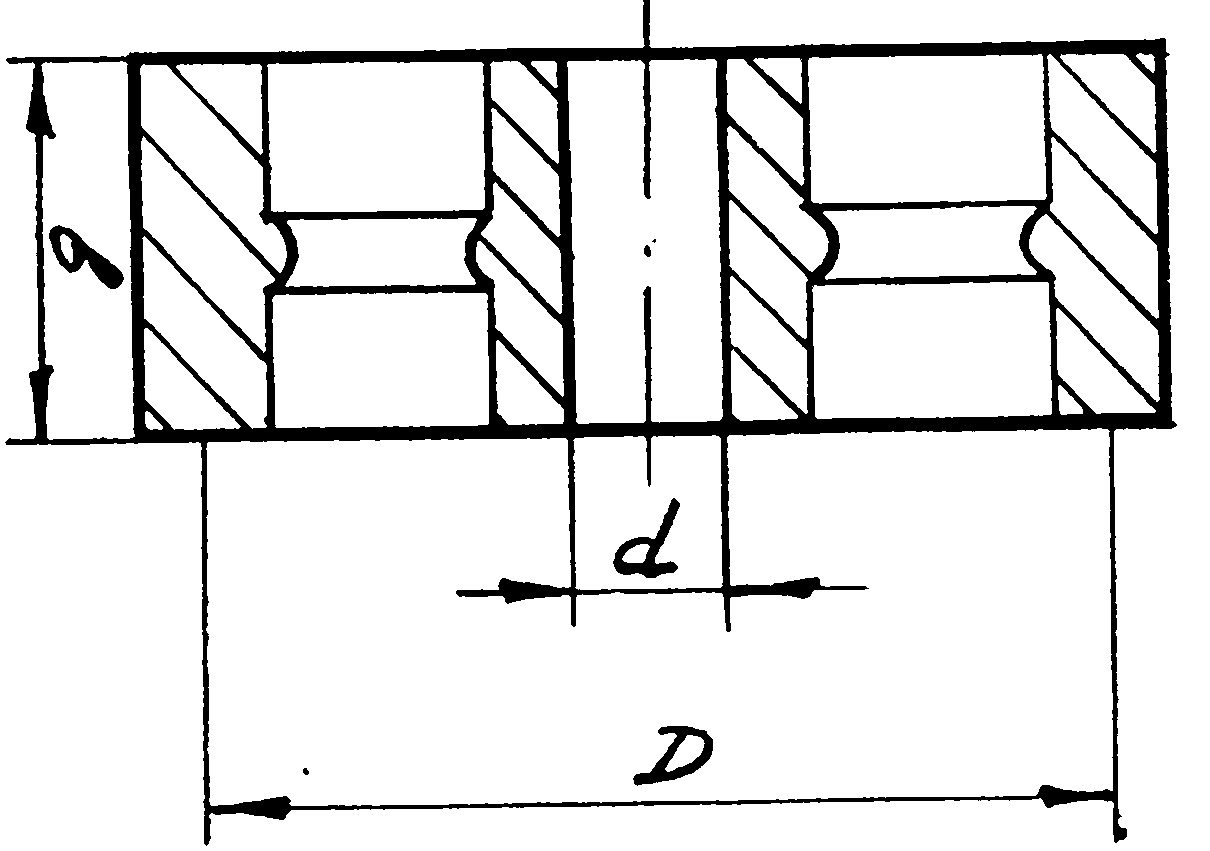
/23.19/

Ескіз маховика

Рис.23.2.

Якщо врахувати моменти інерції маточини і спиць, то:

Iⁿ_max = 1.1 I_max /23.20/

Вираз тD² називається маховим моментом, або характеристикою махови­ка. Задаючись діаметром D маховика, величина якого визначається з конструктивних міркувань, можна легко визначити масу маховика. Щоб запобігти небезпеці можливого розриву маховика, його діаметр виби­рають таким, щоб колова швидкість на ободі не перевищувала допусти­мої, для матеріалу маховика величини. Наприклад, для чавунного махо­вика допустима швидкість V = ЗО м/с.

Якщо маховик встановити не на вхідній ланці механізму, а на якій-небудь і-й його ланці, то з умови рівності кінетичних енергій маємо:

Звідки:

/23.21/

де - динамічний момент інерції маховика, встановленого на і-й ланці; ω_і кутова швидкість цієї ланки.

Якщо між вхідною ланкою і двигуном встановлено редуктор з пере­даточним числом U_Р , то момент інерції маховика на валу двигуна буде:

/23.22/

Необхідна, потужність двигуна на вхідній ланці:

N_дв = M_p * ω_cp, /23.23/

де М_р = у * μ_М.

Механізм з маховиком при усталеному русі працює таким чином. В тих положеннях механізму /в більшості при холостому ході/, коли мо­мент рушійних сил більший за момент сил опору /М_р>М_оп/ збільшуєть­ся кутова швидкість вхідної ланки і тоді, маховик, завдяки своєму значному динамічному моменту інерції, сприймає надлишок кінетичної енергії механізму і не дозволяє кутовій швидкості надмірно зростати. В положеннях механізму /в більшості при робочому ході/, коли момент сил опору більший за момент рушійних сил / М_оп > М_р /, маховик віддає накопичену кінетичну енергію, протидіючи зменшенню кутової швидкості вхідної ланки. Отже, призначення маховика - це регулювання в заданих межах періодичних коливань кутової швидкості вхідної ланки механізму при усталеному русі. Крім того, маховик дозволяє зменшити потрібний рушійний момент, а значить зменшити і необхідну потужність двигуна.