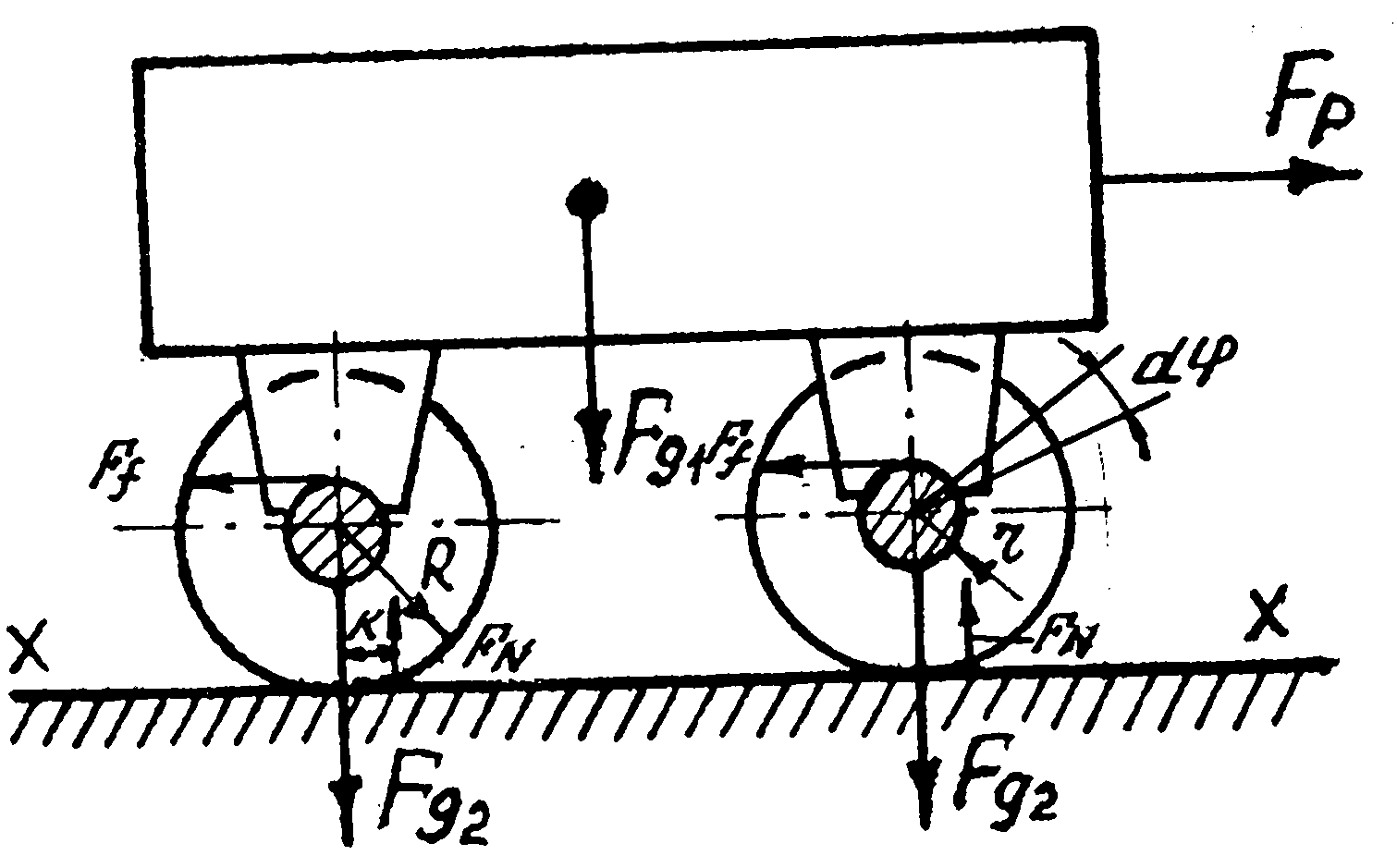
17.3.2. Переміщення вантажу на візку.

Знайдемо горизонтальну рушійну силу F_ρ , необхідну для рівно­мірного переміщення візка з вантажем, сила тяжіння якого F_g1, a сила тяжіння кожного із коліс F_g2, /рис. 17.5/. Позначимо радіуси: колеса R , цапфи r .

Прирівняємо елементарну роботу рушійної сили F_ρ на елемен­тарному переміщенні dx до суми елементарних робіт від моменту тертя кочення коліс відносно площини x - x і від моменту тертя ков­зання в цапфах коліс, отримаємо: А_р=A_x-x+A_fц.

Вантаж на візку

Рис.17.5

/17.33/

Знайдемо елементарне переміщення

/17.34/

Підставимо в рівняння робіт /17.33/ значення dx із /17.34/, отримаємо:

/17.35/

звідси маємо:

/17.36/

Подамо ряд значень коефіцієнту тертя кочення K при певних умовах тертя:

Умови тертя Коефіцієнт К, мм

Стальні бандажі коліс залізничних вагонів відносно рейок 0.5...0.55

Дерево відносно дерева 0.5...1.3

Загартовані стальні кульки і ролики в під­шипниках кочення 0.01

Колеса візків із залізними шинами відносно асфальту 6 Те саме відносно піску 15...30

Лекція 18.

Сили інерції в механізмах.

План лекції:

18.1. Загальні положення.

18.2. Визначення сил інерції ланок плоских механізмів.

18.3. Зведення сил інерції ланки до центру коливання.

18.4. Метод заміщених точок.

18.І. Загальні положення.

Внаслідок руху ланок механізму з прискореннями в кінематичних парах виникають додаткові динамічні зусилля. Для визначення цих зу­силь кожну ланку механізму слід зрівноважити прикладанням до неї у відповідній точці фіктивної сили і фіктивного моменту пари сил, які за величиною рівні силі і моменту пари сил, що визивають прискорений рух ланки. Цю фіктивну силу називають масовою силою, або силою інерції F_і, а фіктивний момент пари сил - моментом пари сил інер­ції M_i.

Слід підкреслити, що ніякої сили інерції F_і і ніякого моменту пари сил інерції M_i до ланки в дійсності не прикладено. Сила F_і момент M_i не мають ніякого фізичного змісту, а в розрахунках ви­конують роль не більше, ніж чисто математичних величин, за допомогою яких враховується вплив прискореного руху ланок на додаткові дина­мічні зусилля в кінематичних парах.

18.2. Визначення сил інерції ланок плоских механізмів.

Ланка механізму складається з окремих матеріальних точок, прис­корення яких в загальному випадку складного руху різні. Тому різні і елементарні сили інерції, умовно прикладені в цих точках. Система елементарних сил інерції матеріальних точок ланки, яка здійснює плоскопаралельний рух і має площину симетрії, паралельну площині ру­ху, зводиться до головного вектора F_і, який прикладений у центрі мас ланки, і до головного моменту M_i пари сил інерції.

Головний вектор сил інерції:

/18.1/

де т - маса ланки, кг; - вектор повного прискорення центра мас S ланки, м/с². З рівності /18.1/ випливає, що сила інерції F_і ви­мірюється в Н. Напрям сили інерції F_і. протилежний напряму вектора прискорення . На це вказує знак "-" в /18.1/.

Момент M_i пари сил інерції спрямований протилежно кутовому прискоренню ε і визначається за формулою:

/18.2/

де І_s – динамічний момент інерції ланки, що дорівнює добутку маси т ланки на квадрат його радіуса інерції ρ_Ѕ відносно центра мас Ѕ

/18.3/

Момент інерції І_s вимірюють в кгм², а кутове прискорення ε – в рад/с². Oтже, момент М_і пари сил інерції вимірюється в НМ. Площина, в якій він діє, паралельна площині руху ланки.