36.1. Особенности составления дифференциальных уравнений в прикладных задачах

Необходимым этапом решения любой прикладной задачи является построение математической модели изучаемого объекта или процесса. Обыкновенные дифференциальные уравнения первого порядка составляют основу простых, но весьма распространенных математических моделей, применяемых в самых разных областях науки и техники. Причина состоит в том, что многие законы физики, механики и других фундаментальных наук, используемые для количественного описания реальных объектов и процессов, устанавливают связь между величинами и их бесконечно малыми приращениями, т.е. дифференциалами. Иными словами, применяемые при решении прикладных задач фундаментальные законы часто предоставляют структуру используемых соотношений между зависимыми и независимыми переменными, близкую или совпадающую со структурой обыкновенного дифференциального уравнения.

Однако формальное использование известных законов в прикладных задачах обычно не дает желаемого эффекта. Дело в том, что каждая прикладная задача имеет свои особенности, требующие осмысления и, как правило, обоснованного упрощения и выделения основных влияющих факторов прежде, чем удается применить тот или иной закон для построения математической модели. Поскольку цель решения прикладной задачи состоит в установлении соотношений между конечными значениями зависимых и независимых переменных, то желательно, чтобы обыкновенные дифференциальные уравнения, входящие в математическую модель, допускали интегрирование ипредставление решения в элементарных функциях. Это условие далеко не всегда выполнимо, но поиск разумного компромисса между сложностью реального объекта или процесса и желаемой простотой их описания является лейтмотивом математического моделирования – одного из наиболее перспективных направлений прикладной математики.

Таким образом, составление входящих в математическую модель обыкновенного дифференциального уравнения требует сочетания знаний в конкретной прикладной области и достаточно высокой математической культуры. После получения решения прикладной задачи важно уметь осмыслить и проанализировать полученный результат, дать ему практическую интерпретацию и попытаться сделать полезные выводы, направленные на совершенствование рассматриваемого объекта или процесса.

36.2. Задачи, приводящие к решению дифференциальных уравнений

Простейшие обыкновенные дифференциальные уравнения рассматривали в своих работах еще И. Ньютон и Г. Лейбниц. Именно Г. Лейбниц ввел в 1676 году термин «дифференциальные уравнения». Задачу решения обыкновенного дифференциального уравнения И. Ньютон трактовал как обратную по отношению к нахождению производной для заданной функции, а вычисление неопределенного интеграла он считал частным случаем этой задачи. Для Ньютона как создателя основ математического естествознания такой подход к восстановлению функции по зависимости между функцией и ее производными был вполне логичным, поскольку большинство известных в науке закономерностей может быть выражено в форме дифференциальных уравнений.

Рассмотрим пример. Тело массой 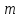падает под действием силы тяжести 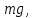где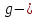ускорение свободного падения и силы сопротивления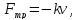пропорциональной скорости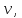где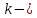коэффициент сопротивления. Найти зависимость скорости движения тела от времени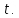

Используя второй закон Ньютона, составим обыкновенное дифференциальное уравнение, описывающее движение тела

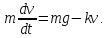
Имеем дифференциальное уравнение первого порядка, разрешенное относительно производной имеющей механический смысл ускорения движения рассматриваемого тела. Можно проверить подстановкой, что решением этого обыкновенного дифференциального уравнения является совокупность функций

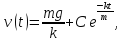
где 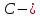произвольная постоянная.

Если в момент времени 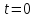тело начинает падение с начальной скоростью 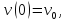то

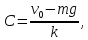
и тогда

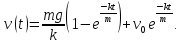
Кроме того, это обыкновенное дифференциальное уравнение имеет решение 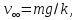к которому стремятся привсе решения вне зависимости от значения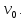

Рассмотрим пример. Из точки 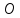под углом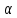к горизонту бросают с заданной начальной скоростью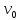тело массой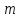так, что оно падает под прямым углом на наклонную плоскость, проходящую через точку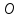и образующую с горизонтом заданный угол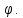Считая углы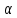и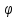острыми, найти угол

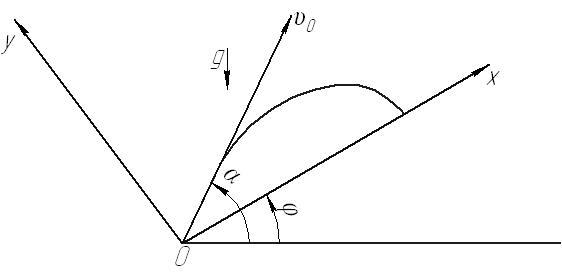
Рис. 64

Поместим в точку 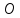начало прямоугольной декартовой системы координат, направив ось абсцисс 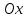вдоль наклонной плоскости. Согласно второму закону Ньютона, уравнения движения тела имеют вид:

Это обыкновенные дифференциальные уравнения второго порядка, разрешенные относительно старшей производной. Они имеют решение:

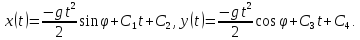
В уравнение входят четыре произвольных постоянных 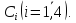Поэтому для выбора из бесконечного множества возможных решений единственного решения, описывающего действительное движение рассматриваемого тела, необходимо использовать сведения о положении и скорости тела в начальный момент времени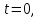однозначно определяющие эти произвольные постоянные. Так как при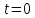тело находится в начале координат, т.е.

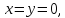то,

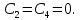
Дифференцируя, получаем

С учетом заданного при 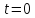значения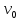скорости тела имеем

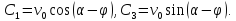
Подставляя найденные выражения для произвольных постоянных в

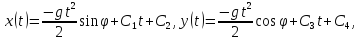
запишем

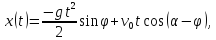
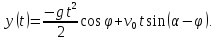
Полученное решение содержит пока еще неизвестное значение угла 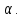Это значение можно найти, приняв во внимание, что тело падает на наклонную плоскость под прямым углом, т.е. в момент времени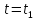падения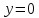и проекция скорости тела на координатную ось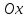равна нулю. Учитывая, что

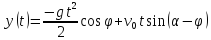
имеем

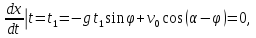
Из условия

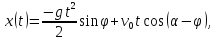
используя полученное выражение для 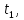имеем

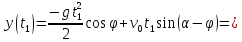
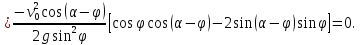
Поскольку по смыслу задачи 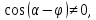то равно нулю выражение в квадратных скобках

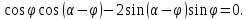
Отсюда после тригонометрических преобразований получаем

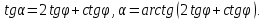
Рассмотрим пример. Человек, находящийся в точке 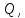движется вдоль оси ординат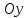в положительном направлении и тянет тяжелый предмет, расположенный в точке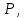за веревку постоянной длины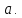

Пусть на плоскости 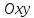в начальный момент времени точка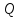находится в начале координат, а точка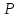имеет координаты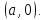Составим обыкновенное дифференциальное уравнение траектории точки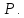

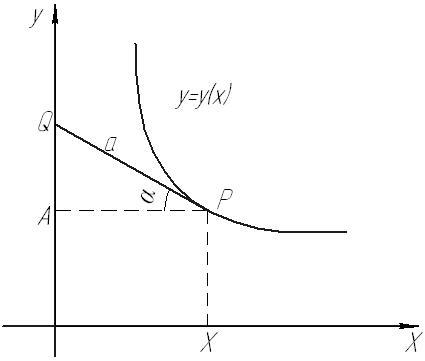
Рис. 65

Траектория точки

Обозначим через 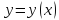уравнение искомой траектории точки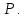Из условия задачи следует, что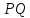является касательной к этой траектории в точке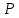с координатами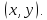Длина отрезк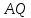аравна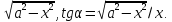Принимая во внимание геометрический смысл производной, т.е.

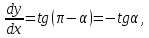
получаем обыкновенное дифференциальное уравнение первого порядка

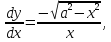
разрешенное относительно производной. Одним из решений этого дифференциального уравнения является функция, которая задает хорошо известную плоскую кривую – трактрису

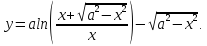
Рассмотрим пример. Сосуд, наполненный жидкостью, вращают с угловой скоростью 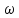вокруг оси 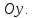Жидкость в сосуде образует воронкообразную полость, границей которой является поверхность вращения некоторой кривой, которая описывается уравнением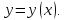Найдем форму этой поверхности.

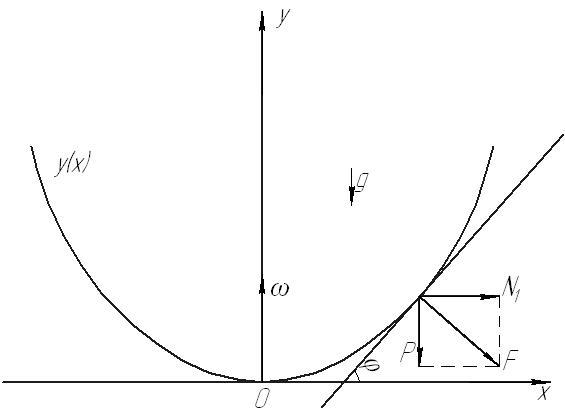
Рис. 66

Поверхность вращения кривой

Рассмотрим частицу на поверхности полости, имеющую массу 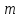и координаты 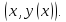Во вращающейся вместе с жидкостью системе координатчастица покоится. В этом случае равнодействующая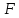силы тяжестии центробежной силы инерции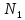с абсолютными значениями соответственно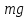и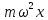ортогональна поверхности вращения. Тогда

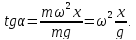
Но в силу геометрической интерпретации производной 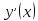как углового коэффициента касательной к графику функции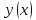имеем

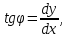
и поэтому

Решая это линейное однородное дифференциальное уравнение с начальным условием 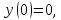получаем

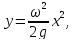
т.е. границей полости является параболоид вращения.

Рассмотрим пример. Составим дифференциальное уравнение, описывающее колебание некоторого конкретного маятника. Предельно идеализируя явление, считая, что движение происходит по прямой, пренебрегая сопротивлением среды, отвлекаясь от физических свойств маятника, получим дифференциальное уравнение

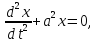
решение которого имеет вид

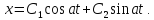
Это решение лишь грубо приближенно описывает явление.

Если учесть сопротивление среды и считать его пропорциональным скорости, то получим уравнение

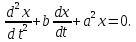
Считая 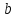малой величиной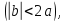получим следующее решение

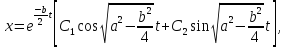
но и этот ответ является лишь довольно грубым приближением.

Если учесть, что движение происходит не по прямой, а по дуге окружности, то уравнение значительно усложнится и примет вид

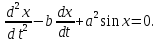
Данное уравнение лишь приближенно описывает процесс, в нем неточно учтен закон сопротивления среды и математический маятник рассматривается как материальная точка, не учтено действие возмущающих сил различного происхождения.

В этом примере, учитывая все новые и новые факторы, мы изменяли дифференциальное уравнение, описывающее изучаемое явление.

Дифференциальное уравнение, описывающее явление с учетом лишь основных, определяющих явление факторов, мало отличаются от дифференциальных уравнений, точно или хотя бы более точно описывающих тот же процесс.

Учитывая лишь основные факторы, мы исходим из предположения, что малое изменение уравнения лишь мало изменяет его решения.

Однако это основное предположение не всегда справедливо. Возьмем хотя бы уравнения

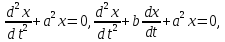
где постоянная величина 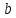мала. Сравним решения этих уравнений

Для небольшого промежутка времени 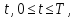решения этих двух уравнений, соответствующие одним и тем же начальным условиям, будут мало отличаться друг от друга, при достаточно малом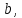но с возрастанием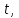как бы мало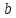ни было, решения этих уравнений все больше и больше будут отличаться друг от друга.

Решения первого уравнения периодические, решения же второго дают 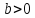затухающие колебания и при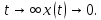

Если же 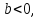то решения второго уравнения неограниченно возрастают по абсолютной величине при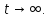

Таким образом, малое изменение правой части может даже качественно менять характер решения.

Решая конкретную задачу, мы ищем решение, удовлетворяющее определенным начальным условиям, однако эти начальные данные являются результатами некоторого измерения и вычисляются с некоторой погрешностью. Поэтому, можно пользоваться такими приближенными начальными данными только исходя из предположения, что малое изменение начальных данных незначительно изменит решение, т.е. решения непрерывно зависят от начальных данных.

Из всего выше сказанного можно сделать вывод: составив уравнение, описывающее какое-нибудь конкретное явление, необходимо помнить, что оно является лишь приближенным, что начальные данные, параметры и вид уравнения могут изменяться, если учесть ранее отброшенные факторы, или уточнить уже учтенные, или точнее измерить начальные данные и т.д.

Контрольные вопросы

1. В чем состоит особенность составления дифференциальных уравнений в прикладных задачах?

2. Привести примеры задач, приводящих к решению дифференциальных уравнений.

Лекция №37. Числовые ряды

37.1. Определение ряда. Сходимость. Сумма ряда.

37.2. Необходимый признак сходимости ряда.

37.3. Достаточные признаки сходимости ряда.