
- •Министерство сельского хозяйства Российской Федерации
- •Фгбоу впо «Самарская государственная сельскохозяйственная академия»
- •Е. В. Бунтова
- •Математика
- •Введение
- •2.1. Формулы Крамера
- •2.2. Обратная матрица
- •2.3. Матричная запись системы линейных алгебраических уравнений и ее решение методом обратной матрицы
- •2.4. Элементарные преобразования матрицы
- •2.5. Ранг матрицы
- •3.1. Теорема Кронекера-Капелли
- •3.2. Метод Гаусса решения систем m линейных уравнений с n неизвестными
- •3.3. Общее, базисное и частное решение систем линейных алгебраических уравнений.
- •3.4. Однородные системы линейных алгебраических уравнений
- •4.2. Линейные операции над векторами.
- •4.3. Декартова система координат
- •4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме
- •4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме
- •4.6. Применение векторного произведения векторов к решению задач
- •4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме
- •4.8. Применение смешанного произведения векторов к решению задач
- •5.1. Линейное пространство
- •5.3. Разложение вектора по базису. Линейные пространства
- •6.1. Линейные преобразования
- •6.2. Собственные значения и собственные векторы матрицы
- •6.3. Свойства собственных векторов матрицы
- •7.1. Уравнение линии на плоскости. Прямая линия и различные формы ее уравнений на плоскости
- •Свойства прямой в евклидовой геометрии.
- •Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось в точкеи образующая уголс положительным направлением оси
- •Уравнение прямой в отрезках.
- •Нормальное уравнение прямой.
- •7.2. Взаимное расположение двух прямых на плоскости
- •7.3. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых
- •8.1. Каноническое уравнение окружности и ее основные характеристики
- •8.2. Каноническое уравнение эллипса и его характеристики
- •8.3. Каноническое уравнение гиперболы и ее характеристики
- •8.4. Каноническое уравнение параболы и ее характеристики
- •8.5. Исследование кривых второго порядка
- •9.1. Плоскость и ее уравнения
- •9.2. Общее уравнение плоскости и его частные виды
- •9.3. Угол между плоскостями. Условие параллельности и перпендикулярности двух плоскостей
- •9.4. Нормальное уравнение плоскости
- •10.1. Уравнение прямой в пространстве
- •10.2. Условия параллельности и перпендикулярности, прямых в пространстве
- •10.3. Взаимное расположение прямой и плоскости в пространстве
- •11.1. Общая теория поверхностей второго порядка
- •11.2. Классификация поверхностей второго порядка
- •11.3. Расположение поверхностей второго порядка
- •12.1. Определение функции. Функциональная зависимость. Область определения функции и способы ее задания
- •12.2. Графическое изображение функции. Классификации функций
- •12.3. Числовые последовательности и их роль в вычислительных процессах. Ограниченные и неограниченные последовательности
- •12.4. Сходимость числовых последовательностей
- •12.5. Предел функции. Односторонние пределы
- •12.6. Основные теоремы о пределах функции
- •13.1. Первый, второй замечательные пределы и их применение к раскрытию неопределенностей. Бесконечно малые и бесконечно большие функции
- •13.2. Непрерывность функции в точке и на интервале
- •13.3. Классификация точек разрыва функции
- •14.1. Определение производной функции
- •14.2. Геометрический и механический смысл производной
- •14.3. Основные правила дифференцирования
- •14.4. Производная обратной, параметрически заданной функции
- •14.5. Производная показательно-степенной функции.
- •15.1. Теоремы Ферма, Ролля, Лагранжа, Коши
- •15.2. Правило Лопиталя
- •15.3. Дифференциал функции
- •15.4. Применение дифференциала к приближенным вычислениям
- •15.5. Производные и дифференциалы высших порядков
- •16.1. Экстремум функции. Возрастание и убывание функции
- •16.2. Точки перегиба функции и участки выпуклости и вогнутости графика функции
- •16.3. Асимптоты графика функции
- •16.4. Общая схема исследования функции и построение ее графика
- •17.1. Определение функции многих переменных. Область определения функции многих переменных
- •17.2. Частные производные и дифференциалы первого и высших порядков
- •17.3. Теорема о смешанных производных
- •17.4. Производная по направлению
- •18.1. Касательная плоскость и нормаль к поверхности
- •18.2. Необходимое и достаточное условия экстремума функции двух переменных
- •18.3. Условный экстремум функции двух переменных. Наибольшее и наименьшее значения функции на замкнутом множестве
- •18.4. Метод множителей Лагранжа
- •19.1. Первообразная функции
- •19.2. Неопределенный интеграл и его свойства
- •19.3. Таблица основных интегралов
- •19.4. Интегрирование методом замены переменной
- •20.1. Интегрирование по частям
- •20.2. Интегрирование функций, содержащих квадратный трехчлен
- •21.1. Интегрирование элементарных дробей
- •21.2. Интегрирование рациональных дробей
- •22.1. Интегрирование методом замены переменной
- •22.2. Интегрирование по частям
- •22.3. Интегрирование с помощью универсальных подстановок
- •23.1. Линейные и дробно-линейные иррациональности
- •23.2. Квадратичные иррациональности
- •24.1. Задачи, приводящие к понятию определенного интеграла
- •24.2. Определение определенного интеграла
- •24.3. Свойства определенного интеграла. Теорема Коши о существовании определенного интеграла
- •24.4. Формула Ньютона-Лейбница
- •25.1. Геометрические приложения определенного интеграла
- •25.2. Физические приложения определенного интеграла
- •25.3. Методы приближенного вычисления определенного интеграла
- •26.1. Несобственные интегралы с бесконечными пределами интегрирования
- •26.2. Несобственные интегралы от неограниченных функций
- •26.3. Признак сходимости несобственных интегралов (признак сравнения)
- •27.1. Постановка задачи интегрирования функции многих переменных
- •27.2. Двойной интеграл и его свойства
- •27.3. Сведение двойного интеграла к повторному. Изменение порядка интегрирования
- •28.1. Геометрический смысл двойного интеграла
- •28.2. Физические приложения двойного интеграла
- •29.1. Определение криволинейного интеграла
- •29.2. Вычисление криволинейных интегралов первого и второго рода. Условия независимости криволинейного интеграла от пути интегрирования
- •29.3. Формула Грина
- •30.1. Комплексные числа и их изображение на плоскости
- •30.2. Модуль и аргумент комплексного числа
- •30.3. Различные формы записи комплексного числа. Формула Эйлера. Алгебраические действия над комплексными числами
- •31.1. Задачи, приводящие к составлению и решению дифференциальных уравнений
- •31.2. Дифференциальные уравнения первого порядка. Теорема Коши. Понятие об общем и частном решении дифференциального уравнения. Дифференциальные уравнения с разделяющими переменными.
- •32.1. Линейные дифференциальные уравнения первого порядка. Физические задачи, приводящие к решению дифференциальных уравнений первого порядка
- •32.2. Однородные дифференциальные уравнения.
- •33.1. Дифференциальные уравнения второго порядка,
- •33.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •34.1. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •34.2. Особенности интегрирования неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью. Метод вариации произвольной постоянной
- •35.1. Нормальная система дифференциальных уравнений
- •35.2. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами
- •36.1. Особенности составления дифференциальных уравнений в прикладных задачах
- •36.2. Задачи, приводящие к решению дифференциальных уравнений
- •37.1. Определение ряда. Сходимость. Сумма ряда
- •37.2. Необходимый признак сходимости ряда
- •37.3. Достаточные признаки сходимости ряда
- •38.1. Достаточный признак сходимости знакочередующихся рядов
- •38.2. Абсолютная и условная сходимость знакопеременных рядов
- •39.1. Функциональные ряды
- •39.2. Степенные ряды
- •39.3. Теорема Абеля
- •40.1. Разложение некоторых элементарных функций в ряды Тейлора, Маклорена
- •40.2. Приложение рядов к приближенным вычислениям
- •41.1. Периодические функции
- •41.2. Определение ряда Фурье
- •41.3. Ряды Фурье четных и нечетных периодических функций с произвольным периодом
- •42.1. Множества
- •42.2. Подмножество
- •42.3. Операции над множествами
- •Свойства операций:
- •43.1. Общие понятия теории графов
- •43.2. Теорема Эйлера. Операции над графами
- •43.3. Способы задания графов
- •43.4. Комбинаторика как наука
- •43.5. Сочетания. Размещения. Перестановки
- •44.1. Развитие теории вероятностей как науки
- •44.2. Виды случайных событий
- •44.3. Классическое определение вероятности
- •44.4. Относительная частота
- •44.5. Теорема сложения вероятностей для несовместных событий. Противоположные события
- •44.6. Условная вероятность. Теорема умножения вероятностей
- •44.7. Теорема сложения вероятностей для совместных событий
- •44.8. Формула полной вероятности. Формулы Байеса
- •45.1. Формула Бернулли
- •45.2. Наивероятнейшее число наступлений событий
- •45.3. Локальная теорема Лапласа. Интегральная теорема Лапласа
- •45.4. Вероятность отклонения частоты от постоянной вероятности в независимых событий. Асимптотическая формула Пуассона
- •46.1. Дискретные и непрерывные случайные величины
- •46.2. Формы задания законов распределения случайных величин: ряд распределения, функция распределения, плотность распределения
- •46.3. Свойства функции распределения и функции плотности распределения вероятности появления случайной величины
- •46.4. Вероятность попадания случайной величины на заданный интервал
- •46.5. Числовые характеристики случайной величины.
- •47.1. Закон распределения дискретной случайной величины. Биномиальное распределение дискретной случайной величины
- •47.2. Распределение Пуассона дискретной случайной величины. Простейший поток событий
- •47.3. Закон распределения непрерывной случайной величины. Равномерный закон распределения непрерывной случайной величины
- •47.4. Показательный закон распределения
- •47.5. Нормальный закон распределения непрерывной случайной величины
- •47.6. Вычисление вероятности заданного отклонения. Правило трех сигм
- •48.1. Закон больших чисел и его практическое значение
- •48.2. Центральная предельная теорема Ляпунова
- •48.3. Применение закона больших чисел и центральной предельной теоремы
- •49.1. Генеральная и выборочная совокупности
- •49.2. Статистическое распределение выборки
- •49.3. Эмпирическая функция распределения
- •49.4. Полигон и гистограмма
- •50.1. Определение статистических оценок параметров распределения
- •50.2. Виды статистических оценок параметров распределения
- •50.3.Надежность статистических оценок параметров распределения.
- •51.1. Статистическая гипотеза
- •51.2. Статистический критерий
- •51.3. Критерий согласия Пирсона
- •51.4. Критерий Колмогорова
- •51.5. Критерий проверки гипотезы о равенстве дисперсий
- •51.6. Критерий сравнения двух выборочных средних
- •51.7. Критерий Вилкоксона проверки гипотезы об однородности двух выборок
- •52.1. Однофакторный дисперсионный анализ
- •52.2. Двухфакторный дисперсионный анализ
- •53.1. Корреляционная зависимость
- •53.2. Линейная парная регрессия
- •53.3. Оценка значимости параметров связи
- •54.1. Понятие о нелинейной регрессии
- •54.2. Корреляционное отношение
- •54.3. Ранговая корреляция
- •Задания для практических занятий по материалу лекций
- •Словарь терминов и определений
- •Алфавитно-предметный указатель
- •Рекомендуемая литература
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера-Снедекора
- •Критические точки критерия Вилкоксона
- •Оглавление
- •Бунтова Елена Вячеславовна математика
- •446442, Самарская обл., пгт. Усть-Кинельский, ул. Учебная, 2
- •443068, Г. Самара, ул. Песчаная, 1
Министерство сельского хозяйства Российской Федерации
Фгбоу впо «Самарская государственная сельскохозяйственная академия»
Е. В. Бунтова
Математика
Учебное пособие
Самара 2012
ББК 22.11 Я7
УДК 51(075)
Б-91
Рецензенты:
канд. пед. наук, доцент кафедры «Математика»
ФГБОУ ВПО «Орловский государственный аграрный университет»
Е. В. Александрова;
канд. пед. наук, доцент кафедры «Математика и теоретическая механика»
ФГБОУ ВПО «Оренбургский государственный аграрный университет»
И. Н. Дементьева
Бунтова, Е. В.
Б-91 Математика: учебное пособие. – Самара: РИЦ СГСХА, 2012. – 459 с.
Учебное пособие включает курс лекций по разделам дисциплины «Математика» в соответствии с рабочей программой для направления подготовки «Агроинженерия» и примерные задания для практических занятий по соответствующим темам лекций. Издание служит формированию у студентов аппарата фундаментальной математической подготовки, как основы изучения и практических приложений общественно-полезных и специальных дисциплин.
Представлены основные понятия математики и их приложения в различных областях. В настоящее время математика служит теоретическим фундаментом большинства технических и естественнонаучных дисциплин. Овладение ее методами и умение применять их на практике необходимо для каждого естествоиспытателя.
Учебное пособие предназначено для студентов, обучающихся по направлению подготовки «Агроинженерия» и молодых педагогов.
© Бунтова Е. В., 2012
© ФГБОУ ВПО «Самарская государственная
сельскохозяйственная
академия», 2012
Введение
Математика – наука о количественных отношениях и пространственных формах действительного мира.
Это самая древняя наука, она стала складываться во втором тысячелетии до нашей эры. Уже строители египетских пирамид владели математическими методами и знаниями.
Окончательно как наука математика была оформлена в третьем веке Евклидом в его бессмертных «Началах». Сложившись, она не перестает развиваться, разрабатываются новые методы, открываются иные применения, совершенствуется символика и научный аппарат.
Одновременно с развитием методов и отраслей математики происходило ее внедрение в другие науки. Благодаря использованию математических методов уже не только обрабатывались показания приборов и результаты экспериментов, но стали создаваться математические модели различных процессов и систем.
Таким образом, используя математический подход, можно проникнуть в еще не исследуемые области физического мира, создать модели малоизученных явлений.
Сила математики именно в ее способности создавать все более высокие абстракции, оперировать ими, изучать их особенности и закономерности.
Последние десятилетия ознаменовались бурным развитием средств и методов вычислительной математики. Математическое моделирование позволяет рассчитать с помощью методов вычислительного эксперимента такие процессы, которые даже не доступны к постановке опыта (управляемый термоядерный синтез, физика лазеров и т.д.).
На сегодняшний день возможно математическое прогнозирование состояния и эволюционного развития различного рода сложных систем.
Этим определяется место математики в системе высшего профессионального образования.
Целью учебного пособия «Математика» является формирование у студентов системы компетенций для решения профессиональных задач по эффективному использованию основных законов естественнонаучных дисциплин в профессиональной деятельности; применение методов математического анализа и моделирования; готовности систематизировать и обобщать информацию по формированию и использованию ресурсов предприятия; готовности к обработке результатов экспериментальных исследований; способности осуществлять сбор и анализ исходных данных для расчета и проектирования.
Лекция №1. Матрицы. Определители и их свойства
Понятие о решении системы линейных алгебраических уравнений.
Матрицы.
Алгебра матриц: сложение, вычитание, умножение на число, произведение.
Определители второго и третьего порядков и их свойства.
Теорема Лапласа о разложении определителя по элементам строки (столбца).
Понятие о решении системы линейных алгебраических уравнений
Система
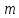 линейных
уравнений с
линейных
уравнений с
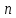 переменными
имеет вид
переменными
имеет вид
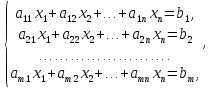
где
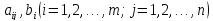 -произвольные
числа, называемые соответственно
коэффициентами
при переменных и свободными членами
уравнений.
-произвольные
числа, называемые соответственно
коэффициентами
при переменных и свободными членами
уравнений.
В более краткой записи с помощью знаков суммирования систему можно записать в виде
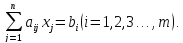
Решением
системы линейных уравнений называется
такая
совокупность
 чисел,
при подстановке которых каждое уравнение
системы обращается в верное равенство.
чисел,
при подстановке которых каждое уравнение
системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Рассмотрим пример. Система уравнений
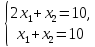
-
совместная и определенная, так как имеет
единственное решение
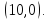
Система
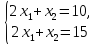
- несовместная.
Система
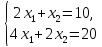
-
совместная и неопределенная, так как
имеет более одного, а точнее бесконечное
множество решений
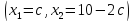 , за
, за
 принимается
любое число.
принимается
любое число.
Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Матрицы
Математика – это набор инструментов. Каждый инструмент служит для выполнения определенной цели. Например, для исследования сложных объектов, которые характеризуются несколькими числами, разработан специальный аппарат, который называется теорией матриц.
Значительная часть математических моделей объектов и процессов записывается в достаточно простой и компактной форме – матричной. Рассматриваемую систему линейных алгебраических уравнений также можно представить в матричной форме.
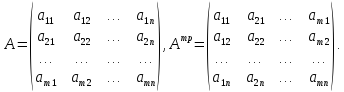
Матрицей
размера
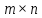 называется прямоугольная таблица чисел,
содержащая m
строк и n
столбцов.
Например,
называется прямоугольная таблица чисел,
содержащая m
строк и n
столбцов.
Например,
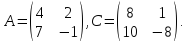
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы
обозначаются заглавными буквами
латинского алфавита:
 ,..,
а элементы
матрицы обозначаются строчными буквами
с двойной индексацией
,..,
а элементы
матрицы обозначаются строчными буквами
с двойной индексацией
 гдеi-номер
строки, j-номер
столбца. Например,
матрица
гдеi-номер
строки, j-номер
столбца. Например,
матрица

С помощью матриц удобно записывать различные физические, экономические, технические и другие данные, выражающие те или иные зависимости.
Матрица может состоять из одной строки или столбца.
Если число строк в матрице равно числу столбцов, то она называется квадратной. Например:
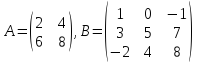 .
.
Элементы
матрицы
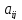 ,
у которых номер столбца равен номеру
строки
,
у которых номер столбца равен номеру
строки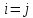 ,
называютсядиагональными.
,
называютсядиагональными.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
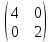 .
.
Если все недиагональные элементы квадратной матрицы равны нулю, а диагональные элементы равны единице, то матрица называется единичной и обозначается буквой E. Например,
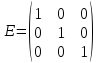 .
.
Алгебра матриц: сложение, вычитание, умножение на число, произведение
Умножение матрицы на число. При умножении матрицы на число получается матрица, элементы которой получены умножением каждого элемента исходной матрицы на это число
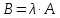
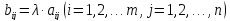 .
.
Рассмотрим пример:
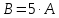 ,
,
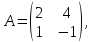
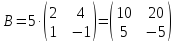 .
.
Следствие: общий множитель всех элементов матрицы можно вынести за знак матрицы.
Сложение и вычитание матриц. Суммой (разностью) двух матриц называется матрица, элементы которой получены с помощью поэлементного сложения (вычитания).
Пример:
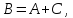
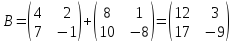 .
.
Вычитание матриц аналогично.
Умножение матриц. В результате умножения двух матриц получается новая матрица. Элементы первой строки, которой получаются путем сложения произведений соответствующих элементов первой строки первой матрицы и первого столбца (затем второго и т.д.) второй матрицы. Аналогично получается вторая, третья, … m – я строка новой матрицы.
Пример:
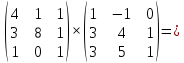
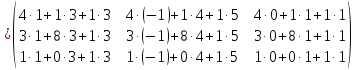

Умножение матрицы на матрицу определено в том случае, если количество столбцов в первой матрице равно числу строк во второй матрице.
Пример:
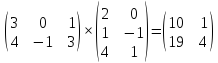 .
.
Возведение матрицы в степень определяется только для квадратных матриц. Важно последовательное умножение матриц.
Пример:
найти
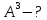 , если
, если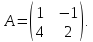
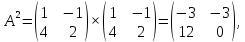

Транспонирование матриц – переход к новой матрице, в которой строки и столбцы поменялись местами с сохранением порядка
Обозначение
Рассмотрим пример:
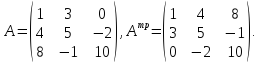
Определители второго и третьего порядков и их свойства
Пусть
А -
произвольная квадратная матрица n-го
порядка
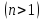

Определителем квадратной матрицы n-го порядка называется число, которое может быть вычислено по элементам матрицы
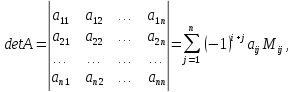
где
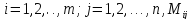 -минор
элемента определителя.
-минор
элемента определителя.
Минором
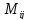 элемента
определителя называется определитель,
который получится, если в исходном
определителе вычеркнуть строку и
столбец, на пересечении которых находится
данный элемент
элемента
определителя называется определитель,
который получится, если в исходном
определителе вычеркнуть строку и
столбец, на пересечении которых находится
данный элемент
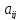 .
.
Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Формула, которая позволяет вычислить определитель матрицы по первой строке
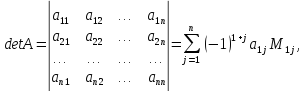
где
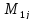 -определитель
квадратной матрицы, полученной из
матрицы
-определитель
квадратной матрицы, полученной из
матрицы
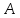 вычеркиванием первой строки иj-го
столбца.
вычеркиванием первой строки иj-го
столбца.
Обозначение
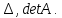
Для определителей второго и третьего порядка легко получить выражения через элементы матрицы.
Определитель второго порядка:
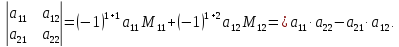
Определитель третьего порядка:

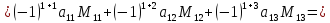
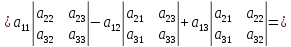
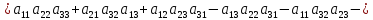
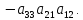
Порядок матрицы является и порядком определителя.
Вычисление определителей второго порядка
Например:
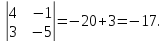
Вычисление определителей третьего порядка.
Определители третьего порядка можно вычислить по правилу треугольника
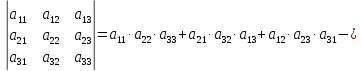
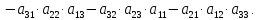
Рассмотрим пример:
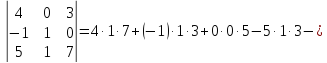
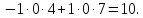
Теорема Лапласа о разложении определителя по элементам строки (столбца)
Определители любого порядка возможно вычислить по теореме Лапласа.
Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения (разложение по элементам какого – либо ряда)
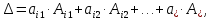
где
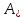 -алгебраические
дополнения элементов строк матрицы.
Или
-алгебраические
дополнения элементов строк матрицы.
Или
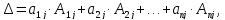
где
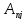 -алгебраические
дополнения элементов столбцов матрицы.
-алгебраические
дополнения элементов столбцов матрицы.
Алгебраическим
дополнением
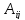 элемента
определителя называется его минор,
взятый со своим знаком, если сумма
индексов
элемента
определителя называется его минор,
взятый со своим знаком, если сумма
индексов
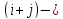 число
четное, и с противоположным знаком, если
сумма индексов (
число
четное, и с противоположным знаком, если
сумма индексов (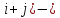 число нечетное
число нечетное

Найдем
алгебраическое дополнение для элемента
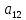 матрицы
матрицы


Каждая
матрица n-го
порядка имеет
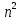 миноров
миноров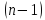 -го
порядка.
-го
порядка.
Найдем
алгебраические дополнения для элементов
первой строки матрицы
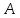
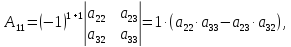
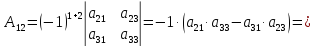
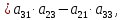
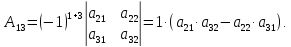
Запишем
определитель матрицы
 и
вычислим с помощью разложения по первой
строке
и
вычислим с помощью разложения по первой
строке

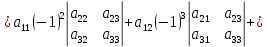
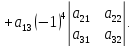
Аналогично можно разложить определитель матрицы по любой строке или столбцу.
Рассмотрим пример.
Вычислим определитель, разложив его по первой строке
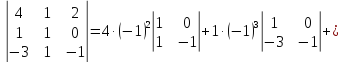
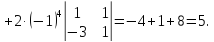
Вычислим определитель, разложив его по второму столбцу
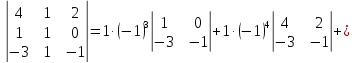
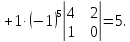
Основные свойства определителей.
При транспонировании матрицы ее определитель не меняется
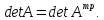
Если в матрице поменять местами два столбца или две строки, то знак определителя поменяется на противоположный, а абсолютная величина останется прежней.
Определитель с одинаковыми столбцами равен нулю.
Общий множитель элементов столбца (или строки) можно вынести за знак определителя
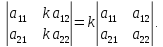
Если в определителе есть столбец, в котором все элементы равны нулю, то определитель равен нулю.
Определитель не изменится, если к элементам столбца прибавить соответствующие элементы другого столбца, умноженные на одно и то же число.
Контрольные вопросы
Дать определение матрицы, пояснить нумерацию элементов. Как определить размер или порядок матрицы?
Как сложить (вычесть) матрицы, умножить на число?
Какие действия с матрицами называют линейными?
Перечислить свойства линейных операций.
Сформулировать правило умножения матриц.
Перечислить свойства произведения матриц.
Дать определение минора
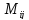 элемента
определителя.
элемента
определителя.Перечислить основные свойства определителей.
Лекция №2. Формулы Крамера. Матричный способ решения систем линейных алгебраических уравнений
2.1. Формулы Крамера.
2.2. Обратная матрица.
2.3. Матричная запись системы линейных алгебраических уравнений и ее решение методом обратной матрицы.
2.4. Элементарные преобразования матрицы.
2.5. Ранг матрицы.
