
- •Министерство сельского хозяйства Российской Федерации
- •Фгбоу впо «Самарская государственная сельскохозяйственная академия»
- •Е. В. Бунтова
- •Математика
- •Введение
- •2.1. Формулы Крамера
- •2.2. Обратная матрица
- •2.3. Матричная запись системы линейных алгебраических уравнений и ее решение методом обратной матрицы
- •2.4. Элементарные преобразования матрицы
- •2.5. Ранг матрицы
- •3.1. Теорема Кронекера-Капелли
- •3.2. Метод Гаусса решения систем m линейных уравнений с n неизвестными
- •3.3. Общее, базисное и частное решение систем линейных алгебраических уравнений.
- •3.4. Однородные системы линейных алгебраических уравнений
- •4.2. Линейные операции над векторами.
- •4.3. Декартова система координат
- •4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме
- •4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме
- •4.6. Применение векторного произведения векторов к решению задач
- •4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме
- •4.8. Применение смешанного произведения векторов к решению задач
- •5.1. Линейное пространство
- •5.3. Разложение вектора по базису. Линейные пространства
- •6.1. Линейные преобразования
- •6.2. Собственные значения и собственные векторы матрицы
- •6.3. Свойства собственных векторов матрицы
- •7.1. Уравнение линии на плоскости. Прямая линия и различные формы ее уравнений на плоскости
- •Свойства прямой в евклидовой геометрии.
- •Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось в точкеи образующая уголс положительным направлением оси
- •Уравнение прямой в отрезках.
- •Нормальное уравнение прямой.
- •7.2. Взаимное расположение двух прямых на плоскости
- •7.3. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых
- •8.1. Каноническое уравнение окружности и ее основные характеристики
- •8.2. Каноническое уравнение эллипса и его характеристики
- •8.3. Каноническое уравнение гиперболы и ее характеристики
- •8.4. Каноническое уравнение параболы и ее характеристики
- •8.5. Исследование кривых второго порядка
- •9.1. Плоскость и ее уравнения
- •9.2. Общее уравнение плоскости и его частные виды
- •9.3. Угол между плоскостями. Условие параллельности и перпендикулярности двух плоскостей
- •9.4. Нормальное уравнение плоскости
- •10.1. Уравнение прямой в пространстве
- •10.2. Условия параллельности и перпендикулярности, прямых в пространстве
- •10.3. Взаимное расположение прямой и плоскости в пространстве
- •11.1. Общая теория поверхностей второго порядка
- •11.2. Классификация поверхностей второго порядка
- •11.3. Расположение поверхностей второго порядка
- •12.1. Определение функции. Функциональная зависимость. Область определения функции и способы ее задания
- •12.2. Графическое изображение функции. Классификации функций
- •12.3. Числовые последовательности и их роль в вычислительных процессах. Ограниченные и неограниченные последовательности
- •12.4. Сходимость числовых последовательностей
- •12.5. Предел функции. Односторонние пределы
- •12.6. Основные теоремы о пределах функции
- •13.1. Первый, второй замечательные пределы и их применение к раскрытию неопределенностей. Бесконечно малые и бесконечно большие функции
- •13.2. Непрерывность функции в точке и на интервале
- •13.3. Классификация точек разрыва функции
- •14.1. Определение производной функции
- •14.2. Геометрический и механический смысл производной
- •14.3. Основные правила дифференцирования
- •14.4. Производная обратной, параметрически заданной функции
- •14.5. Производная показательно-степенной функции.
- •15.1. Теоремы Ферма, Ролля, Лагранжа, Коши
- •15.2. Правило Лопиталя
- •15.3. Дифференциал функции
- •15.4. Применение дифференциала к приближенным вычислениям
- •15.5. Производные и дифференциалы высших порядков
- •16.1. Экстремум функции. Возрастание и убывание функции
- •16.2. Точки перегиба функции и участки выпуклости и вогнутости графика функции
- •16.3. Асимптоты графика функции
- •16.4. Общая схема исследования функции и построение ее графика
- •17.1. Определение функции многих переменных. Область определения функции многих переменных
- •17.2. Частные производные и дифференциалы первого и высших порядков
- •17.3. Теорема о смешанных производных
- •17.4. Производная по направлению
- •18.1. Касательная плоскость и нормаль к поверхности
- •18.2. Необходимое и достаточное условия экстремума функции двух переменных
- •18.3. Условный экстремум функции двух переменных. Наибольшее и наименьшее значения функции на замкнутом множестве
- •18.4. Метод множителей Лагранжа
- •19.1. Первообразная функции
- •19.2. Неопределенный интеграл и его свойства
- •19.3. Таблица основных интегралов
- •19.4. Интегрирование методом замены переменной
- •20.1. Интегрирование по частям
- •20.2. Интегрирование функций, содержащих квадратный трехчлен
- •21.1. Интегрирование элементарных дробей
- •21.2. Интегрирование рациональных дробей
- •22.1. Интегрирование методом замены переменной
- •22.2. Интегрирование по частям
- •22.3. Интегрирование с помощью универсальных подстановок
- •23.1. Линейные и дробно-линейные иррациональности
- •23.2. Квадратичные иррациональности
- •24.1. Задачи, приводящие к понятию определенного интеграла
- •24.2. Определение определенного интеграла
- •24.3. Свойства определенного интеграла. Теорема Коши о существовании определенного интеграла
- •24.4. Формула Ньютона-Лейбница
- •25.1. Геометрические приложения определенного интеграла
- •25.2. Физические приложения определенного интеграла
- •25.3. Методы приближенного вычисления определенного интеграла
- •26.1. Несобственные интегралы с бесконечными пределами интегрирования
- •26.2. Несобственные интегралы от неограниченных функций
- •26.3. Признак сходимости несобственных интегралов (признак сравнения)
- •27.1. Постановка задачи интегрирования функции многих переменных
- •27.2. Двойной интеграл и его свойства
- •27.3. Сведение двойного интеграла к повторному. Изменение порядка интегрирования
- •28.1. Геометрический смысл двойного интеграла
- •28.2. Физические приложения двойного интеграла
- •29.1. Определение криволинейного интеграла
- •29.2. Вычисление криволинейных интегралов первого и второго рода. Условия независимости криволинейного интеграла от пути интегрирования
- •29.3. Формула Грина
- •30.1. Комплексные числа и их изображение на плоскости
- •30.2. Модуль и аргумент комплексного числа
- •30.3. Различные формы записи комплексного числа. Формула Эйлера. Алгебраические действия над комплексными числами
- •31.1. Задачи, приводящие к составлению и решению дифференциальных уравнений
- •31.2. Дифференциальные уравнения первого порядка. Теорема Коши. Понятие об общем и частном решении дифференциального уравнения. Дифференциальные уравнения с разделяющими переменными.
- •32.1. Линейные дифференциальные уравнения первого порядка. Физические задачи, приводящие к решению дифференциальных уравнений первого порядка
- •32.2. Однородные дифференциальные уравнения.
- •33.1. Дифференциальные уравнения второго порядка,
- •33.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •34.1. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •34.2. Особенности интегрирования неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью. Метод вариации произвольной постоянной
- •35.1. Нормальная система дифференциальных уравнений
- •35.2. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами
- •36.1. Особенности составления дифференциальных уравнений в прикладных задачах
- •36.2. Задачи, приводящие к решению дифференциальных уравнений
- •37.1. Определение ряда. Сходимость. Сумма ряда
- •37.2. Необходимый признак сходимости ряда
- •37.3. Достаточные признаки сходимости ряда
- •38.1. Достаточный признак сходимости знакочередующихся рядов
- •38.2. Абсолютная и условная сходимость знакопеременных рядов
- •39.1. Функциональные ряды
- •39.2. Степенные ряды
- •39.3. Теорема Абеля
- •40.1. Разложение некоторых элементарных функций в ряды Тейлора, Маклорена
- •40.2. Приложение рядов к приближенным вычислениям
- •41.1. Периодические функции
- •41.2. Определение ряда Фурье
- •41.3. Ряды Фурье четных и нечетных периодических функций с произвольным периодом
- •42.1. Множества
- •42.2. Подмножество
- •42.3. Операции над множествами
- •Свойства операций:
- •43.1. Общие понятия теории графов
- •43.2. Теорема Эйлера. Операции над графами
- •43.3. Способы задания графов
- •43.4. Комбинаторика как наука
- •43.5. Сочетания. Размещения. Перестановки
- •44.1. Развитие теории вероятностей как науки
- •44.2. Виды случайных событий
- •44.3. Классическое определение вероятности
- •44.4. Относительная частота
- •44.5. Теорема сложения вероятностей для несовместных событий. Противоположные события
- •44.6. Условная вероятность. Теорема умножения вероятностей
- •44.7. Теорема сложения вероятностей для совместных событий
- •44.8. Формула полной вероятности. Формулы Байеса
- •45.1. Формула Бернулли
- •45.2. Наивероятнейшее число наступлений событий
- •45.3. Локальная теорема Лапласа. Интегральная теорема Лапласа
- •45.4. Вероятность отклонения частоты от постоянной вероятности в независимых событий. Асимптотическая формула Пуассона
- •46.1. Дискретные и непрерывные случайные величины
- •46.2. Формы задания законов распределения случайных величин: ряд распределения, функция распределения, плотность распределения
- •46.3. Свойства функции распределения и функции плотности распределения вероятности появления случайной величины
- •46.4. Вероятность попадания случайной величины на заданный интервал
- •46.5. Числовые характеристики случайной величины.
- •47.1. Закон распределения дискретной случайной величины. Биномиальное распределение дискретной случайной величины
- •47.2. Распределение Пуассона дискретной случайной величины. Простейший поток событий
- •47.3. Закон распределения непрерывной случайной величины. Равномерный закон распределения непрерывной случайной величины
- •47.4. Показательный закон распределения
- •47.5. Нормальный закон распределения непрерывной случайной величины
- •47.6. Вычисление вероятности заданного отклонения. Правило трех сигм
- •48.1. Закон больших чисел и его практическое значение
- •48.2. Центральная предельная теорема Ляпунова
- •48.3. Применение закона больших чисел и центральной предельной теоремы
- •49.1. Генеральная и выборочная совокупности
- •49.2. Статистическое распределение выборки
- •49.3. Эмпирическая функция распределения
- •49.4. Полигон и гистограмма
- •50.1. Определение статистических оценок параметров распределения
- •50.2. Виды статистических оценок параметров распределения
- •50.3.Надежность статистических оценок параметров распределения.
- •51.1. Статистическая гипотеза
- •51.2. Статистический критерий
- •51.3. Критерий согласия Пирсона
- •51.4. Критерий Колмогорова
- •51.5. Критерий проверки гипотезы о равенстве дисперсий
- •51.6. Критерий сравнения двух выборочных средних
- •51.7. Критерий Вилкоксона проверки гипотезы об однородности двух выборок
- •52.1. Однофакторный дисперсионный анализ
- •52.2. Двухфакторный дисперсионный анализ
- •53.1. Корреляционная зависимость
- •53.2. Линейная парная регрессия
- •53.3. Оценка значимости параметров связи
- •54.1. Понятие о нелинейной регрессии
- •54.2. Корреляционное отношение
- •54.3. Ранговая корреляция
- •Задания для практических занятий по материалу лекций
- •Словарь терминов и определений
- •Алфавитно-предметный указатель
- •Рекомендуемая литература
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера-Снедекора
- •Критические точки критерия Вилкоксона
- •Оглавление
- •Бунтова Елена Вячеславовна математика
- •446442, Самарская обл., пгт. Усть-Кинельский, ул. Учебная, 2
- •443068, Г. Самара, ул. Песчаная, 1
26.1. Несобственные интегралы с бесконечными пределами интегрирования
В предыдущих лекциях мы рассматривали интегралы от функций, интегрируемых на конечных отрезках интегрирования. На практике возникает необходимость обобщения этих понятий на случаи, когда либо один из концов (или оба) отрезка интегрирования удален в бесконечность, либо функция не ограничена на отрезке интегрирования.
Пусть
функция
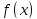 определена на промежутке
определена на промежутке
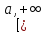 и интегрируема по любому отрезку
и интегрируема по любому отрезку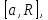 т.е. существует определенный интеграл
т.е. существует определенный интеграл
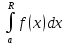
при
любом
 Тогда, если существует конечный предел
Тогда, если существует конечный предел
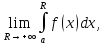
то его называют несобственным интегралом первого рода и обозначают
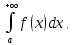
Таким образом, по определению,
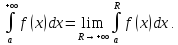
Если данный предел не существует или бесконечен, то несобственный интеграл не существует или расходится.
Аналогично
вводится несобственный интеграл по
промежутку
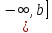
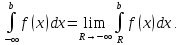
Несобственный интеграл с двумя бесконечными пределами можно определить как сумму выше рассмотренных несобственных интегралов
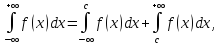
где -любое число, при условии существования обоих интегралов справа.
Геометрический смысл несобственного интеграла первого рода.
Пусть
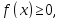 тогда определенный интеграл
тогда определенный интеграл
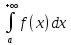
выражает
площадь области, ограниченной сверху
графиком функции
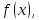 снизу – осью
снизу – осью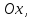 слева
– прямой
слева
– прямой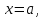 справа –
прямой
справа –
прямой
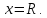
Несобственный интеграл
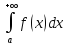
выражает
конечную площадь бесконечной области,
ограниченной сверху графиком функции
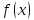 ,
снизу осью
,
снизу осью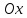 ,
слева прямой
,
слева прямой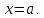
Рассмотрим пример вычисления несобственного интеграла первого рода.
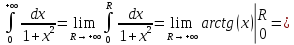
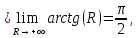
т.е. данный интеграл сходится.
Рассмотрим пример.
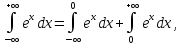
интеграл расходится, так как
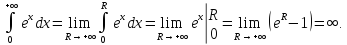
В рассмотренных примерах вычисление несобственного интеграла было основано на его определении.
26.2. Несобственные интегралы от неограниченных функций
Пусть
функция
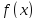 определена на промежутке
определена на промежутке
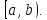 Точку
Точку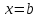 называют особой, если функция
называют особой, если функция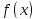 неограниченна в любой окрестности этой
точки, но ограничена на любом отрезке
неограниченна в любой окрестности этой
точки, но ограничена на любом отрезке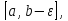 заключенном в
заключенном в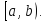 Пусть на любом отрезке
Пусть на любом отрезке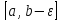 функция
функция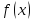 интегрируема, т.е. существует определенный
интеграл
интегрируема, т.е. существует определенный
интеграл
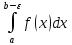
при
любом
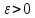 таком, что
таком, что
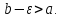 Тогда, если существует конечный предел
Тогда, если существует конечный предел
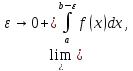
то его называют несобственным интегралом второго рода и обозначают
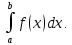
Если предел от данного интеграла не существует или бесконечен, то интеграл не существует и расходится.
Если
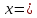 -особая
точка, то несобственный интеграл
определяется так
-особая
точка, то несобственный интеграл
определяется так
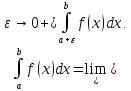
Если
функция
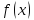 не ограничена в окрестности какой-нибудь
внутренней точки
не ограничена в окрестности какой-нибудь
внутренней точки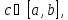 то при условии существования обоих
интегралов справа по определению
то при условии существования обоих
интегралов справа по определению
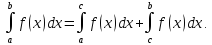
Если
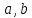 -особые
точки, то если оба интеграла справа
существуют, несобственный интеграл
определяется как сумма
-особые
точки, то если оба интеграла справа
существуют, несобственный интеграл
определяется как сумма
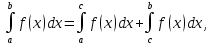
где
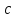 -любая точка из
-любая точка из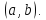
26.3. Признак сходимости несобственных интегралов (признак сравнения)
Если
функции
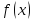 и
и
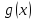 непрерывны на промежутке
непрерывны на промежутке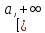 и удовлетворяет на нем условию
и удовлетворяет на нем условию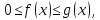 то из сходимости интеграла
то из сходимости интеграла
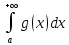
следует сходимость интеграла
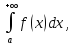
а из расходимости интеграла
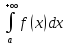
следует расходимость интеграла
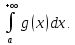
Рассмотрим пример. Исследовать сходимость
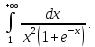
Сравним подынтегральную функцию
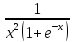
с
функцией
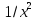 на промежутке
на промежутке Очевидно, что
Очевидно, что
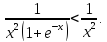
Но интеграл
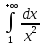
сходится,
так как
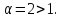 Следовательно, согласно признаку
сравнения сходится и данный интеграл.
Следовательно, согласно признаку
сравнения сходится и данный интеграл.
Рассмотрим пример. Исследовать сходимость
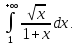
Сравнивая подынтегральную функцию
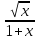
с
функцией
 на промежутке
на промежутке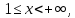 имеем
имеем
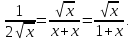
Но интеграл
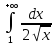
расходится,
так как
 Следовательно, согласно признаку
сравнения и данный интеграл сходится.
Следовательно, согласно признаку
сравнения и данный интеграл сходится.
Контрольные вопросы
Дать определение несобственному интегралу с бесконечными пределами.
Дать определение несобственному интегралу с конечными пределами.
Какие несобственные интегралы называют сходящимися (расходящимися)?
Лекция №27. Двойной интеграл
27.1. Постановка задачи интегрирования функции многих переменных.
27.2. Двойной интеграл и его свойства.
27.3. Сведение двойного интеграла к повторному. Изменение порядка интегрирования.
