9.2. Ортогональная аксонометрическая проекция
9.2.1. Основные свойства ортогональной аксонометрии
Наибольшее распространение в конструкторской практике получили ортогональные аксонометрические проекции. Этот вид аксонометрии в большей степени удовлетворяет условию наглядности, чем косоугольные проекции, поскольку обычно мы рассматриваем предметы расположенные прямо перед нашими глазами. Кроме того при этом достигается больше упрощений, чем в косоугольных проекциях.
В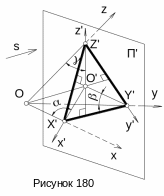
прямоугольной аксонометрии все три
координатные оси пересекают картинную
плоскость П' (рисунок 180). Обозначим точки
пересечения координатных осей x,
y и z с
картинной плоскостью П' соответственно
X', Y' и Z'.
Треугольник X'Y'Z',
по которому плоскость П' пересекает
координатные плоскости натуральной
системы координат называют треугольником
следов, поскольку стороны этого
треугольника являются следами координатных
плоскостей на плоскости П'
Рассмотрим основные свойства ортогональной аксонометрии.
Треугольник следов X'Y'Z' всегда остроугольный.
Это свойство очевидно: декартова система координат пересекается с любой плоскостью (не совпадающей с координатной) по остроугольному треугольнику.
Аксонометрические оси в ортогональной аксонометрии являются высотами треугольника следов.
Справедливость этого утверждения следует из теоремы о проецировании прямого угла. Например, ось Оz и отрезок X'Y', лежащий в картинной плоскости П' (и в тоже время в координатной плоскости хОу) – перпендикулярны. Поэтому и их проекции O'z' и X'Y'=XY также будут перпендикулярны.
Три выходящие из одной точки луча, лежащие в плоскости, только тогда могут являться аксонометрическими осями ортогональной аксонометрии, если они образуют между собой тупые углы.
Действительно, если лучи O'X',O'Y' и O'Z' являются системой аксонометрических осей, то в соответствии со свойством 2 они являются высотами остроугольного треугольника следов X'Y'Z'. При этом известно, что отрезки высот, соединяющих центр О' с вершинами X', Y' и Z', образуют попарно тупые углы.
Показатели искажения в ортогональной аксонометрии равны косинусам углов наклона натуральных осей к картинной плоскости П'.
В самом деле, в случае ортогональной аксонометрии ОО'П', следовательно отрезок О'Х' является ортогональной проекцией отрезка ОХ'. Поэтому u= О'Х'/ ОХ'= cos α. Здесь через α обозначен угол наклона оси х к плоскости П'. Аналогично определятся и показатели искажения v и w, поэтому будем иметь :
u = cos α, v = cos β, w = cos γ. (2)
Следовательно в ортогональной аксонометрии все три показателя искажения ограничены значениями 0 и 1, что соответствует возможным значениям косинуса.
9.2.2. Ортогональная аксонометрия окружности
Довольно часто при выполнении аксонометрических проекций приходится строить эллипсы, в которые проецируются окружности, имеющиеся на комплексном чертеже. Поэтому рассмотрим построение ортогональной проекции окружности, расположенной в какой-либо координатной плоскости (или плоскости параллельной ей).
Для этого вспомним свойства ортогональной проекции окружности, рассмотренные ранее в пункте 27.2. Было выяснено, что у эллипса, являющегося ортогональной проекцией окружности, расположенной в какой-либо координатной плоскости, большая ось равна диаметру окружности d и параллельна прямой уровня этой плоскости, а малая ось равна d cosφ, где φ – угол наклона плоскости окружности к плоскости проекций, и параллельна проекции перпендикуляра к этой плоскости.
Эти свойства указывают способ построения ортогональной аксонометрии окружностей, расположенных в координатных (или параллельных им) плоскостях.
Действительно, если окружность расположена в одной из координатных плоскостей, то перпендикуляром к ее плоскости будет отсутствующая в этой плоскости натуральная координатная ось (рисунок 182).
Поэтому малая ось эллипса, изображающего окружность, лежащую в одной из координатных плоскостей, параллельна аксонометрической проекции натуральной оси, отсутствующей в этой плоскости, а большая ось ей перпендикулярна.
Поскольку величины осей эллипса определяются соотношениями (см.4.5.2):
2α = d; 2b = d cos φ, (3)
то показатель искажения по направлению большой оси эллипса равен единице, а по направлению малой оси равен косинусу угла наклона плоскости окружности к плоскости проекций.
Из рисунка 180 видно, что угол Z'O'O наклона координатной плоскости xOy к картинной плоскости П' является дополнительным углом для угла γ, т.к. в треугольнике Z'O'O угол при вершине О – прямой. Поэтому, обозначив угол Z'O'O как φху, можно записать:
cos φху = sin γ или cos φху =√ (1- cos² γ) = √ (1- w²).
Аналогично можно определить показатели искажения малых осей для других координатных плоскостей. Таким образом получим, что показатели искажения малых осей эллипсов, изображающих окружности, лежащие в координатных плоскостях xOy, xOz и yOz соответственно равны:
cos φху =√ (1- w²); cos φхz = √ (1- v²); cos φуz =√ (1- u²). (4)