105. Основные свойства матрицы структуры.

Свойства М-структуры:

• М-структура это «0;1» матрица, т.к. все ее элементы являются «0/1»;

• М-структура всегда квадратная, т.к. состоит из из квадратичных подматриц. Если в некоторой строке или соответствующем столбце отсутствуют элементы, то М-структура дополняется «0» квадратной подматрицей;

• Главная диагональ М-структуры всегда «0», т.к. компоненты системы не могут быть связаны сами с собой, с точки зрения внешнего описания;

• Если в какой-либо строке М-структуры больше 1 элемента, то это означает что элемент с N строки связан больше чем с одним другим элементом:

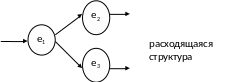
• Если в какой-либо строке М-структуры больше 1 элемента, то это свидетельствует о том, что несколько элементов связаны с одним, имеющим N совпадений с N столбца:

• Если в М-структуры имеется хоть один столбец или строка с «0», то для обеспечения свойства целостности в соответствующем столбце или строке должно быть хоть один значащий элемент, в противном случае М-структура распадается на независимые подматрицы;

• В М-структуре на главной диагональю находятся элементы, определяющие обратные связи в структуре;

• В М-структуре крайний правый верхний и крайний левый нижний элементы, если они значащие – замыкают структуру в кольцо по прямым и обратным связям.

Тороидальные структуры бывают:

• односвязные;

• многосвязные.

Существует два типа связей:

• прямые;

• обратные.

Рассмотренная структура являются элементарной с точки зрения организации вычислительной среды.

106. Моделирование статики динамической системы с последовательным соединением элементов.

Анализ структурной схемы почти всегда дает возможность свести её к трем типам соединения элементов :

1. Последовательная схема.

2. Параллельная схема.

3. Схема с обратной связью.

Рассмотрим построение модели статики системы с последовательной схемой соединения элементов.

Пусть для каждого элемента известна его функция :

Запишем уравнения связей между элементами: .

Существует два подхода для построения модели:

1) Аналитический:

Выход всей системы – выход n-го элемента

Если схема более сложная, то аналитический метод может быть реализован в рамках модели Фогта. Когда математическая модель целостной системы формируется в виде дерева, корень которого – целостная модель.

Графический подход:

Заданы статические условия элементов и схема:

Представим характеристики первых трех элементов.

Прейдем к графическим построениям : возьмем на оси х₁ (.) x’₁ и восстановим перпендикуляр до пересечения с f₁ ; перенесем (.) l’ до пересечения с f₂ и затем до f₃.

Если число элементов > 3, то берем еще 2 элемента и строим характеристики в первом и во втором квадратах, обобщаем характеристику в третьем квадрате и находим общую характеристику последовательной цепи из пяти элементов.

Аналогичные построения будем производить до тех пор, пока не построим общую характеристику всех элементов цепочки.

107. Моделирование статики динамической системы с параллельным соединением элементов (согласное и встречное).

Анализ структурной схемы почти всегда дает возможность свести её к трем типам соединения элементов :

1) Последовательная схема.

2) Параллельная схема.

3) Схема с обратной связью.

Рассмотрим построение модели статики системы с параллельной схемой соединения элементов.

Пусть имеется система, элементы которой имеют параллельную схему соединения.

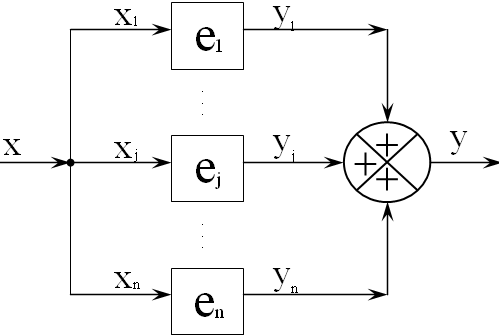
Уравнения связи для входа х:

Аналитический метод: принимаем уравнения выхода: .

Графический метод:

Ординаты по соответствующим точкам суммируются  получается итоговая характеристика.