1 Случай. Дифференциальная модель.

Предположим, что мы берем х₁(t) и изменяем:

х₁(t) ∆ х₁(t)

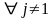, х_j(t) = 0 или х_j(t) = const.

При данных условиях происходит частичное изменение. α – коэффициент частичного эффекта:

;

…….

;

…….

.

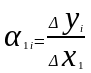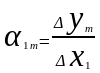Это проводим по всем координатам х. После этого получим матрицу частичных эффектов:

,

,

,

.

Тогда свертка математического описания может быть представлена

.

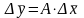В развернутом виде имеем вид:

…….

…….

.

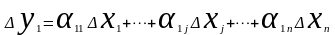
Переход во временную область дает

.

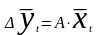Перейдем к бесконечно малым величинам, ∆→0:

…….

…….

.

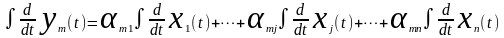Перейдем к свертке:

- приращение дифференциала.

2 Случай. Интегральная модель.

Проинтегрируем систему уравнений, в этом случае α_ij=const, и тогда:

…….

…….

.

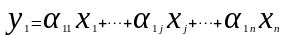
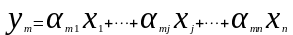Свертка данной системы приводит к записи:

.

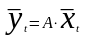3 Случай. Функциональная модель.

На выходе имеются некоторые функции 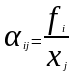, при этом существует условие, что

…….

…….

.

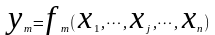В общем случае функциональная модель элемента будет представлена как .

При решении обратной задачи: 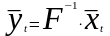. Если мы переходим из детерминированной системы в вероятностную, то все записи справедливы, но с оператором математического ожидания. Все рассмотренные модели по методу О.Лаиге справедливы для линейного представления.

100. Математическое моделирование динамики элемента по аналогии (метод интерпретаций).

Рассмотрим состояние, поведение элемента как компонента некоторой системы, причем параметры связанности входа и выхода

  ;  .

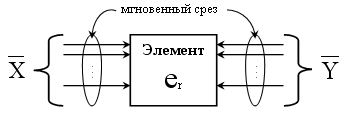
Элемент erсвязан с окружающей средой и взаимодействует.

;

Из среды элемента на вход поступают сигналы x.

Если входной параметр > 1, то создается возможность для воздействия на элемент по этим сигналам

(1) х ; при >1.

Функционирование элемента происходит во времени. В общем случае может рассматриваться поведение элемента на временном интервале - <  < t0 или   (t0 ; t ).

Если поведения элемента зависит от состояния входов на ( -  ;t0), то такой элемент относят к числу элементов с последействием.

В противном случае говорят об элементах без предыстории и поведения элемента рассматривается при   ( t0 ; t ).

Больше рассматриваются элементы без предыстории (без последействия) t > t0.

С учетом изложенного входного сигнала измененного во времени и каждого компонента сигнала и учитывая (1) :

x(t) (2).

Перейдем к теоретико-множественному представлению (2) : множество входных сигналов er образуют пространство входных сигналов , размерностью n, представляемого в виде прямого произведения компонент :

(3).

Каждая координата (3) может принимать множество значений:

если дискретные значения – целочисленный ряд,если непрерывные значения – ряд дейстительный чисел.

С учетом выражения (3) для каждого момента времени  мы можем задать некоторый вектор мгновенных значений координат пространства , которые определяют некоторую точку в рассматриваемом пространстве, которая называется средним значением входных сигналов.

- мгновенное среднее значение координат входных сигналов.

Функционирование элемента будем рассматривать на . Для этого временного интервала рассматриваем изменение . Все точки в пространстве , являющиеся составляющими (определяемыми) образуют входной процесс. На интервале имеем место входной процесс .

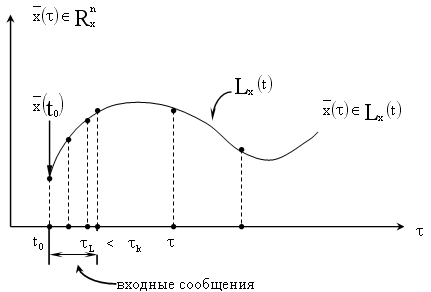
Если задано x(t0) и некоторых значения для точек , то мы имеем входное сообщение, подаваемое на элемент er.

По заданному сообщению может осуществить предсказание поведения входного процесса.