101. Математическое моделирование элементов систем по методу пространства состояний.

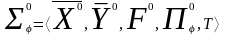
МПС предлагает рассмотрение трех процессов:

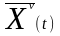
Они связаны и взаимодействуют. Ограничения не вводятся, т.к. рассматривается некая универсальная модель.

1. Модель входного процесса:

Рассматриваем входной процесс и область определения входного процесса Х:

= (Х_{1, … ,} Х_{j, … ,} Х_n),

- размерность области определения.

Координата Х может быть изменена во времени:

_t= (Х₁^t_{, … ,} Х_j^t_{, … ,} Х_n^t).

Каждая из координат Х_j может принимать совокупность значений:

;

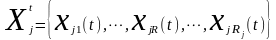- прямое произведение задает полное множество входных сигналов.

Для каждого момента t мы будем иметь входное воздействие:

,

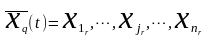где - точка в области определения входного процесса, число таких точек равно N=(n*R_j). Если число таких точек упорядочить во времени, то

t

Совокупность точек – представляет входной процесс, а выражение определяют математическая модель входного процесса. Каждое значение каждой компоненты векторного множества изменяется

x_j(t)_min ≤ x_j(t) ≤ x_j(t)_max, .

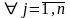2. Модель выходного процесса.

Область значений Y. Пусть выход многомерный и зададим его вектором :

_t= (Y₁^t_{, … ,} Y_j^t_{, … ,} Y_n^t);

;

.

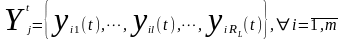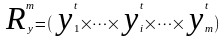- мгновенное значение, которое указывает точку в области значений.

-

- совокупность выражений определяют математическую модель выходного процесса.

Графическая интерпретация аналогична предыдущей, но в зеркальном отображении.

3. Модель в состоянии процесса.

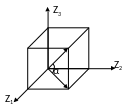Внутреннее состояние Z – происходит перемещение точки в трехмерном пространстве.

По каждой координате изменение происходит по соответствующему виду состояний:

Z₁ = (П¹₁,…,П¹_q1,…, П¹_Q1);

Z₂ = (П²₁,…,П²_q2,…, П²_Q2);

Z₃ = (П³₁,…,П³_q3,…, П³_Q3).

В общем случае внутреннее состояние объекта можно определить некоторым вектором состояний:

Z = (Z_1, Z_2, Z₃),

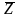= (Z_1,…, Z_к,…, Z_К), где – вектор состояний.

Полная совокупность состояний объекта определится посредством прямого произведения:

;

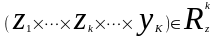Если мы изменим состояние, то

,

.

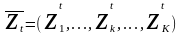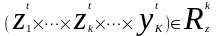В каждый момент времени каждое значение принимает свое значение параметра и образует совокупность:

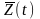= Z₁(t),…, Z_k(t),…, Z_K(t).

Совокупность таких точек образует траекторию движения (состояния):

Рассмотрим поведение элемента на временной оси:

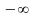
Выбираем начало t₀ (t = 0). При рассмотрении поведения элемента на интервале , то говорят, что элемент имеет предысторию, тогда в описание элемента мы должны включать предысторию. Если анализ описания начинается с 0, то модель описывает поведение элемента без предыстории.При рассмотрении процесса вход и выход процесс может выступать как процесс x(t_j) t_j = (0,1,…,n) – мгновенное значение.

С учетом (*) мы можем записать входной процесс х(t₀), х(t_j), х(τ) или .

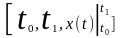Аналогичное представление осуществим и для выходного процесса .

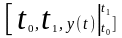Раздел VIII: Математическое моделирование сложных систем

1. Понятие сложной системы.

Сложная система, составной объект, части которого можно рассматривать как системы, закономерно объединённые в единое целое в соответствии с определенными принципами или связанные между собой заданными отношениями. Понятием Сложная система пользуются в системотехнике, системном анализе, операций исследовании и при системном подходе в различных областях науки, техники и народный хозяйства. Сложную систему можно разделить (не обязательно единственным образом) на конечное число частей, называемое подсистемами; каждую такую подсистему (высшего уровня) можно в свою очередь разделить на конечное число более мелких подсистем и т. д., вплоть до получения подсистем первого уровня, т. н. элементов сложной системы, которые либо объективно не подлежат разделению на части, либо относительно их дальнейшей неделимости имеется соответствующая договорённость. Подсистема, т. о., с одной стороны, сама является сложной системой из нескольких элементов (подсистем низшего уровня), а с другой стороны - элементом системы старшего уровня.

Система. Под системой принято понимать совокупность взаимосвязанных и взаимодействующих компонент, интегральное поведение которых направленно на реализацию целевой функции, присущей системе в целом.

Объединяющим (интегрирующим) является цель.

Взаимосвязанность компонент определяет морфологическую (структурную) целостность.

Взаимодействие, реализуемое через обмен сигналами (вещественными, энергетическими, информационными), между компонентами обеспечивает функциональную целостность.

Компоненты системы. Под компонентами в теории систем принято понимать части целостной системы – элементы и подсистемы различных рангов, т.е. термин компоненты заменяет термин и подсистемы, и элемента.

Элемент наименьшая, неделимая в данном рассмотрении часть системы. Это структурный компонент и в системе рассматривается по схеме «вход – выход». Это функциональный компонент.

Подсистема – такая часть системы, для которой рассматривается ее внутреннее устройство – структура и функционирование.

Подсистемы и элементы образуют структуру целостной системы.