Классификация элементов по морфологическим признакам.
Функциональное описание элемента.
В зависимости от сложности объекта он может быть моно- или полифункциональным. Соответствующим образом характеризуется и описание.
Рассмотрение начнем с функционального описания элемента.
;
Выделим элемент ev из системы:
Элемент ev:
Связь элемента со средой происходит через специально выделенные точки, которые называют полюсами. Входные полюса:
Для выхода имеем множество выходных полюсов:
Физические элементы систем.
Под математическом моделированием понимают способ исследования различных процессов путём изучения явлений, имеющих различное физическое содержание, но описываемых одинаковыми математическими соотношениями.
Поскольку при моделировании нет необходимости сохранять размеры сооружений, скорости течения жидкостей и газов, нагрузки на элементы конструкций и т.д. имеется возможность получить существенный выигрыш во времени и стоимости исследования. Однако условия моделирования физических элементов выбираются не абсолютно произвольно. Между элементом-оригиналом и объектом-моделью должны быть сохранены некоторые соотношения подобия, вытекающие из закономерностей физической природы явлений, получаемых путем моделирования для оценки свойств элемента-оригинала.
Определение метода «математическое моделирование».
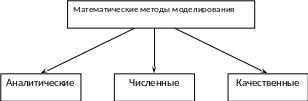
Математическое моделирование — процесс построения и изучения математических моделей.
Аналитические методы предполагают получение на основе математического описания решения (результата) в общем виде. Такое решение справедливо при любых ограничениях и исходных данных. Формульное представление → преобразование из одной формулы в другую.
Численные методы дают возможность получить количественный результат только для некоторых определенных исходных данных и ограничений.
Количественные методы позволяют определить некоторые общие свойства результата и подхода к его получению.
Понятие «математическая модель».
Математическая модель — это математическое представление реальности.
Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.
Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):
находящаяся в некотором объективном соответствии с познаваемым объектом;
способная замещать его в определенных отношениях;
дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.
По учебнику Советова и Яковлева: «модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.» «Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием.» «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.»
По Самарскому и Михайлову , математическая модель — это «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д.» Существует в триадах «модель-алгоритм-программа». «Создав триаду „модель-алгоритм-программа“, исследователь получает в руки универсальный, гибкий и недорогой инструмент, который вначале отлаживается, тестируется в пробных вычислительных экспериментах. После того, как адекватность (достаточное соответствие) триады исходному объекту установлена, с моделью проводятся разнообразные и подробные „опыты“, дающие все требуемые качественные и количественные свойства и характеристики объекта.» (с.7-8)
По монографии Мышкиса: «Перейдем к общему определению. Пусть мы собираемся исследовать некоторую совокупность S свойств реального объекта a с помощью математики (здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т. д.). Для этого мы выбираем (как говорят, строим) „математический объект“ a' — систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого и т. д.,— исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах S. В этих условиях a' называется математической моделью объекта a относительно совокупности S его свойств.» (с.8)
По Севостьянову А. Г: «Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.»
Несколько менее общее определение математической модели, основанное на идеализации «вход — выход — состояние», заимствованной из теории автоматов, даёт Wiktionary: «Абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия.»
Наконец, наиболее лаконичное определение математической модели: «Уравнение, выражающее идею.»