52. Аутокаталичность как свойство больших (сложных) систем.

Наиболее адекватен при создании и функционировании больших и сложных систем. Суть в больших и сложных системах для устойчивой их работы необходимо, чтобы функционирование структуры реализующее определенные функции в одной из частей сложной системы повторялись при необходимости реализации подобных функций и в других частях этой системы. В случае не выполнения сформированного условия система функционирует неустойчиво, а в определенных случаях может распадаться или разрушаться.

53. Принцип аутокаталичности.

Принцип аутокаталичности. В системах, состоящих из большого числа однородных, упорядоченно связанных и взаимодействующих компонент, функциональные структуры, выполняемые одной из систем повторяется при реализации подобных функций и в других компонентах, что в случае невыполнения своих функций одной из таких компонент системой эти же функции может выполнить другая компонента системы.

54. Принцип управляемости.

Принцип управляемости. При релевантности осведомительной и адекватности управляющей информации изменение состояния компонент – подсистем и элементов, а так же модели в целом должны осуществляться таким образом, чтобы в условиях изменяющейся внешней среды движение управляемого объекта (модели) было ориентировано в направлении достижения оптимального значения целевой функции. Иначе говоря модель должна быть подстраиваемой под конкретную ситуацию и быть в каком-то смысле универсальной.

55. Принцип комплексности.

Принцип комплексности. Предполагает всестороннее, многоаспектное, многофакторное рассмотрение системы (объекта оригинала), как неоднородной, взаимосвязанной и взаимодействующей совокупности компонент избирательно вовлеченных в единое целое в соответствии с определенными исходными концепциями, причем согласованное функционирование исходных компонент направлено на достижение единой глобальной цели. Комплексный подход представляет методологическую базу для анализа и синтеза сложных систем.

56. Принцип системности.

Принцип системности. При решении задач моделирования охватывает две стороны явления. С одной стороны он связан с объектом-оригиналом через целостность, с другой с экспертом по моделированию системным подходом. Рассмотрение или исследование объекта-оригинала и создание модели этого объекта должно осуществляться исходя из представлений о способности составляющих такой объект компонент (подсистем и элементов), а как следствие и моделей этих компонент, вступать в такого рода отношения (взаимосвязи и взаимодействия), в результате которых порождаются целостные свойства системы (модели) в том числе и эмерджентные.

57. Определить совокупность принципов, используемых при создании модели в зависимости от фаз жизненного цикла модели.

58. Определить совокупность принципов, используемых при решении задачи моделирования, в зависимости от фаз жизненного цикла задачи.

Жизненный цикл задачи (ЖЦЗ) можно свести к следующим фазам:

1. Возникновение и развитие задачи (латентная, скрытая);

2. Описание задачи;

3. Постановка задачи;

4. Решение задачи;

5. Оптимизация результата решения;

6. Прекращение существования задачи.

Рисунок 6.1 Фазы ЖЦЗ.

Задача – нечто явно видное, но что-то нужно для получения конечного результата.

Задача: P = < ∑_p⁰ , Z_p, C_p, I_p >

• ∑_p⁰ – объект. Этот компонент по существу дает возможность сформировать описательное содержание задачи.

• Z_p – цели, задачи. Компонент трактуется как образ или модель конечного результата, на который направлено решение задачи. Мысленный образ желаемого, предполагаемого предмета потребности.

• С_p – условия, при которых реализуется задача;

I_p ={I_p} – совокупность данных и знаний. I_p = <K_p, D_p>

Условие задачи: C_p = < M_p, A_p, P_p, Г_p >

• M_p – метод;

• А_p – алгоритм;

• Р_p – программа;

Г_p – требования к конечному результату. Г_p = <Q_wp, E_fp>

Анализ применимости принципов моделирования осуществляется на основе, уже рассмотренной в предыдущей работе, диаграмме модельной деятельности.

Рисунок 2.1 Диаграмма принципов моделирования.

Верхняя половина диаграммы отражает непосредственно модельную сторону деятельности, а нижняя – объектную.

Левая часть определяет теоретические методы познавательно-созидательной деятельности объектом оригиналом и его моделью. Правая часть – экспериментальную.

I-ый квадрант определяет модельную экспериментальную деятельность, а также обратно – экспериментально-модельную.

II-ой квадрант – теоретически-модельную и модельно-теоретическую деятельности.

III-ий квадрант – теоретически-объектная и объектно-теоретическая деятельности.

IV-ый квадрант – объектно-экспериментальная и экспериментально-объектная деятельности.

Косвенная связь T→M отражает влияние теории на модель, т.е. использование существующей теории для создания модели.

Косвенная связь М→Т отражает влияние модели на существующую теорию, изучив модель, эксперт вносит изменения в теорию.

Косвенная связь Э→М отражается в проведение эксперимента над моделью, с целью анализа данной модели на пригодность, адекватность для реализации поставленной цели.

Косвенная связь М→Э отражает влияние модели на экспериментальную деятельность, поскольку результаты эксперимента могут способствовать пересмотру и перепланировке проведения экспериментов.

Косвенная связь Т→∑ показывает применимость теории для исследования объекта оригинала.

Косвенная связь ∑→Т показывает влияние объекта на теорию. После изучения объекта оригинала может возникнуть надобность в корректировке существующей теории, поскольку она может не отвечать необходимым требованиям.

Косвенная связь Э→∑ отражается в проведении эксперимента над объектом оригиналом с целью его изучения.

Косвенная связь ∑→Э отражает влияние объекта на планирование эксперимента. Изучения объекта оригинала может натолкнуть на новую идею проведения эксперимента, т.е. на перепланировку имеющегося эксперимента.

Раздел IV: Методы моделирования

1. Физическое моделирование систем: принципы и методы.

- физическое моделирование на основе геометрического подобия;

- физическое моделирование на основе аналогового подобия.

Методы физического моделирования основаны на том, что между объектом-оригиналом и моделью установлены отношения замещения, полного или частичного, в соответствии с целями и задачами моделирования, причем модель всегда имеет физическую форму реализации. Физическое моделирование в зависимости от степени соответствующей объекту оригиналу, имеет ряд реализующихся между собой методов.

Методы физического моделирования могут быть представлены в простейшем виде следующей схемой:

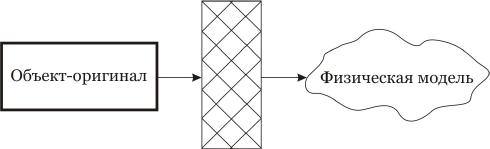
Соответствие между объектом и моделью в методах физического моделирования

При физическом моделировании объекту оригиналу ставится в соответствие другой физический объект – модель, причем по отношению к оригиналу модель может быть одной физической природы с оригиналом или отличной от нее. В первом случае имеют место модели геометрического подобия, во втором аналогового.

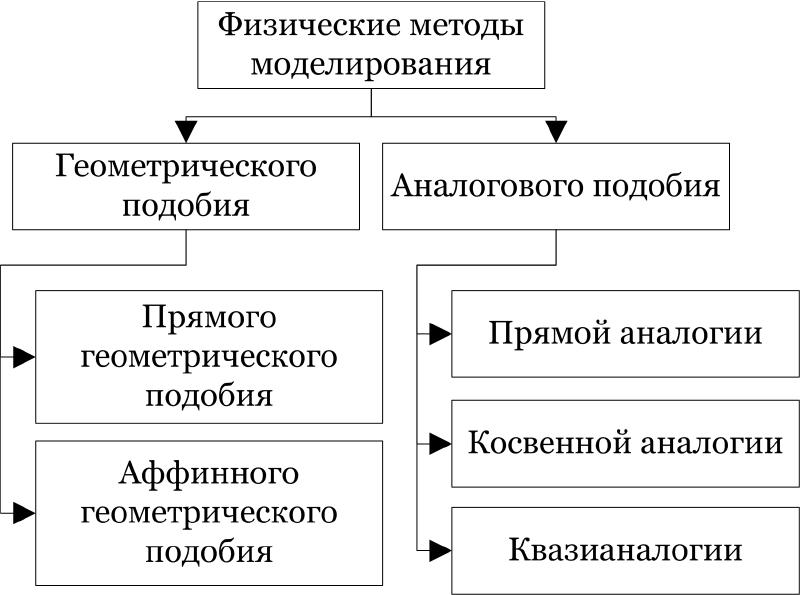
Классификация методов физического моделирования

Метод геометрического подобия

Наиболее близка объекту модель геометрического подобия. В этом случае оригинал и его модель имеют одну и ту же физическую природу, однако различия между ними определяются посредством масштабирования. В тех случаях, когда коэффициент подобия между оригиналом и моделью по всем степеням свободы равны, имеют место модели прямого геометрического подобия. В случае, где условия равнозначности коэффициентов пропорциональности нарушаются, т.е. некоторые коэффициенты имеют разное значение, имеет место аффинное геометрическое подобие.

При геометрическом подобии между оригиналом и моделью устанавливаются отношения геометрической размерности, определяемые соответствующими коэффициентами, одинаковыми для всех степеней свободы оригинала, отображаемых в модели (по всем направлениям одинаковый коэффициент пропорциональности).

Достоинства методов: исследователь работает в привычной для него области знаний, он имеет дело со знакомыми предметами и объектами, используются соответствующие профилю исследования теории, а так же экспериментальные методы, по существу, исследователь работает с тем же объектом оригиналом, но представленным в более удобной форме.

Недостатки методов:

• При моделировании на основе методов геометрического подобия имеет место большая трудоемкость создания модели.

• Все опасности связанные с испытанием модель копии остаются такими же, как и при испытании оригинала и имеют ограниченное применение.

Методы аналогового подобия

Эта группа методов предполагает наличие реального или идеального объекта-оригинала или иного, замещающего исходный объект, имеющий физическую реализующую модель. Однако при моделировании по аналогии, физическая природа модели не совпадает с физической природой оригинала.

Между объектом оригиналом и его физической моделью существует промежуточная стадия – математическое описание.

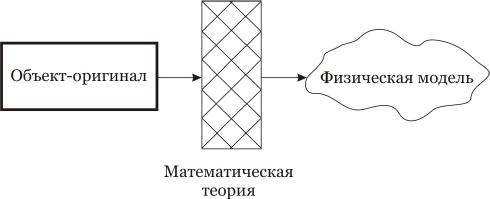
Соответствие между объектом и моделью в методах аналогового подобия

Моделирование по аналогии реализуется по следующей технологии: имеется объект оригинал (физический объект). Объекту оригиналу на основе его свойств ставится в соответствие содержательное описание (реализуемое на естественном языке, в него могут включаться таблицы, графики и т.п.). Далее осуществляется аппроксимация и формализация содержания описания и на основе его, на математическом языке строится математическая модель описания.

При моделировании по аналогии широкое распространение получили методы, при которых, независимо от исходной предметной области модель аналог строится в электрической системе. Разработана большая группа методов моделирования по аналогии на основе критериев подобия.

Принято различать следующие системы аналогий:

1. Электромеханические аналогии (ЭМА).

2. Электротепловые аналогии (ЭТА).

3. Электрогидродинамические аналогии (ЭГА).

4. Электромагнитные аналогии (ЭМгА).

Для всех систем существует соответствующая интерпретация и критерии подобия.

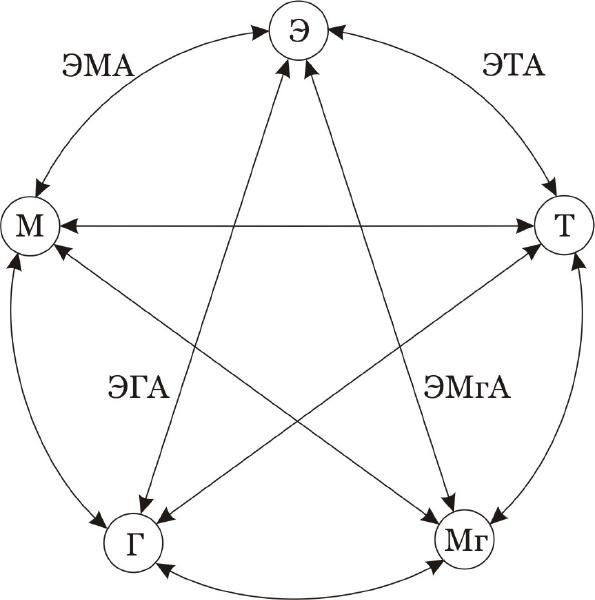
Общая схема метода аналогий

59. Математическое моделирование систем: принципы и методы.

- моделирование по схеме «вход - выход»;

- методы детерминированного моделирования;

- методы вероятностного моделирования.

Функциональный анализ проводится по схеме вход-выход:

• анализ входных сигналов;

• анализ множества входных откликов (реакций);

• анализ отображения входа в выход (функции объекта);

• анализ параметров и характеристик выходных реакций, входных сигналов и функции отображения (F) на статистическом и динамическом уровне.

Формирование ответов на перечисленные выше задачи анализов определяет внешнее задачи объекта моделирования.

Математическая модель – формальная система, представленная совокупностью символов и совершено строгих правил оперирования этими символами, вместе с интерпретацией свойств оригинала, посредством констант, переменных и т.п.

Математические методы определяются:

1. Внутренними свойствами оригинала, которые в соответствии с целями и задачами моделирования требуется отобразить в модели.

2. Языками математического описания.

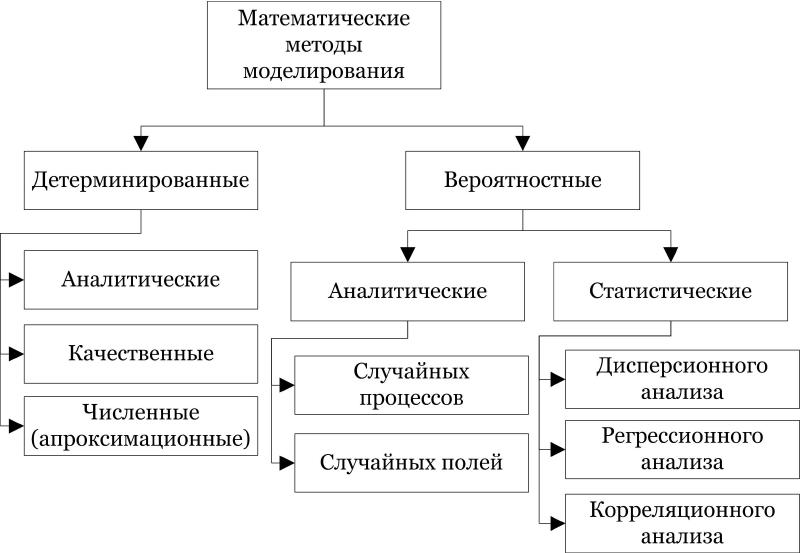
Классификация методов математического моделирования

Детерминированные методы моделирования

Детерминированные методы различаются в зависимости от математических схем, начиная от алгебраических, матричных, дифференциальных, интегральных, интегро-дифференциальных.

Метод аналитического математического моделирования включает в себя все математические модели, для которых возможно аналитическое решение (в общем виде), например, решение квадратного уравнения.

Методы численного математического моделирования. Эта группа методов дает возможность получить результаты моделирования для частных случаев, когда общее решение невозможно, а для некоторых совокупностей значений исходных данных примерные решения возможны, степень приближения определяется требованиями к качеству результата.

Методы качественного математического моделирования, когда имеется математическое описание оригинала, но в силу сложности нельзя получить ни аналитического, ни численного решения. В то же время, в зависимости от значений аргументов возможно качественно определить тенденцию развития решения и установить зоны, где располагается решение, например максимальная и минимальная грань, правую и левую границы решения, характер решения – линейный или нелинейный, положительный или отрицательный.

Вероятностные методы моделирования.

Вероятностные методы основаны на уравнениях 1-го и 2-го порядка – для описания случайных процессов и выше второго порядка – для моделирования случайных полей. Их называют аналитическими методами.

Статистические методы моделирования

Кроме аналитических применяются также статистические методы, основанные на экспериментальных данных.

Метод дисперсионного анализа применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную (отклик). В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные), а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.

Метод регрессионного анализа — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной. Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные.

Метод коррелиционного (ковариационного) анализа — совокупность методов математической статистики, относящихся к анализу моделей зависимости среднего значения некоторой случайной величины Y одновременно от набора (основных) качественных факторов F и (сопутствующих) количественных факторов X. Факторы F задают сочетания условий, при которых были получены наблюдения X,Y, и описываются с помощью индикаторных переменных, причем среди сопутствующих и индикаторных переменных могут быть как случайные, так и неслучайные (контролируемые в эксперименте).

Метод факторного анализа заключается в методики комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Метод средне-мерного моделирования, в его основу закладываются методы определения среднего значения результата.

60. Специальные методы моделирования.

- имитационное моделирование;

- моделирование по схеме Монте-Карло

- эволюционное моделирование.

Метод имитационного моделирования предполагает воспроизведение на основе логико-математических методов, при помощи специального алгоритма, поведения, функционирования объекта-оригинала в рамках реальных или представляемых режимов.

Имитационное моделирование учитывает внутренние и внешние социальные факторы, предполагает воздействие на объект-оригинал.

В структуру имитационного моделирования входят:

• Моделирующий алгоритм

• Формирователь случайных факторов

• Регистратор результатов моделирования

Метод имитационного моделирования основан на описании реальных или гипотетических процессов, в реальных или идеальных объектах оригиналах посредством логико-математических схем и воспроизведении этих схем посредством программ в компьютерной среде. Основой имитационного моделирования выступает моделирующий алгоритм. Этот алгоритм по операционно (по операциям) отражает процесс функционирования. Для описания таких процессов могут использоваться как реальные, так и предполагаемые характеристики и параметры объектов моделирования.

Имитационное моделирование чаще всего используется для исследования или изучения сложных процессов или систем с учетом случайных факторов и случайных характеристик. Тем не менее, на основе имитации могут моделироваться и детерминированные процессы. Математические схемы дают лишь формальное описание. Совокупность математических и логических методов дает возможность сформировать алгоритм.

1. Моделирование систем массового обслуживания.

2. Модели гибели и размножения, на основе уравнения Вольтера или потоков Вольтера. Есть стандартное математическое описание и стандартное представление в виде алгоритмов.

3. Моделирование на основе генных алгоритмов. Рассматривается тот или иной объект, процесс, в его развитии, онтогенетическое развитие объекта и модели объекта. Более высокий уровень отражения природы – уровень популяций. Эволюция популяций составляет существо эволюционного моделирования.

Моделирование по методу Монте-Карло.

Использование псевдо-случайных чисел для вычисления площадей сложных фигур, для воспроизведения некоторых функций, представления в интегральной форме.

Метод Монте-Карло - общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи.

Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики (например, развитие методов численного интегрирования) и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественностью получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.

Эволюционное моделирование в подавляющем числе случаев используется для оптимизации задач моделирования.

Эволюционное моделирование использует признаки теории Дарвина для построения интеллектуальных систем (методы группового учета, генетические алгоритмы). Является частью более обширной области искусственного интеллекта — вычислительного интеллекта.

Эволюционное моделирование это уже достаточно сложившаяся область, в которой можно выделить:

1. модели возникновения молекулярно-генетических информационных систем;

2. моделирование общих закономерностей эволюции (Эволюционные алгоритмы). Это системы, которые используют только эволюционные принципы. Они успешно использовались для задач типа функциональной оптимизации и могут легко быть описаны на математическом языке. К ним относятся эволюционные алгоритмы, такие как Эволюционное программирование, Генетические алгоритмы, Эволюционные стратегии, Генетическое программирование;

3. эволюционные модели. Это системы, которые являются биологически более реалистичными, чем эволюционные алгоритмы, но которые не оказались полезными в прикладном смысле. Они больше похожи на биологические системы и менее направлены на решение технических задач. Они обладают сложным и интересным поведением, и, видимо, вскоре получат практическое применение. К этим системам относят так называемую искусственную жизнь.

4. прикладное эволюционное моделирование.