80. Классификация языков описания объектов.

Язык – совокупность элементов, посредством которых осуществляется информационный обмен в биологических, технических или биотехнических системах. Язык должен включать алфавит, грамматику и синтаксис, на основе которых формируются слова, фразы, предложения, т.е. более крупные лексические (в естественном языке) и синтаксические (в искусственном языке) группы. Язык – знаковая система, предназначенная для информационного обмена. Алфавит – слова – фразы (словосочетания) – предложения – тексты.

Языки описания:

3.1. Естественные. Описания, составленные на естественном языке, принято называть лингвистическими моделями (описательные модели на естественные языки). Естественный узкопрофессиональный язык – надмножество естественного языка. Естественные языки мало используются для моделирования, т.к. они не способны к преобразованию, не однозначны. При моделировании они используются только на начальном этапе, при составлении первичного описания.

3.2. Искусственные. Они более применимы для моделирования. Пример искусственного языка – эсперанто (международный язык).

Искусственные языки ориентированы на различные технические приложения:

а) логический язык.

б) математический язык.

в) графический язык.

г) знаково-символьный язык.

Модели в соответствии с языком описания.

а) Логические модели: модели булевой алгебры логики, предикатные модели.

б) Математические модели: простые арифметические и алгебраические конструкции, вероятностные модели.

Y^(r) = { y_i^(r), i=1, m(r)}

X^(r) = { x_j^(r), j=1, n(r)}

в) Графические модели: структурные модели, модели типа блок-схема, структурная схема алгоритма, сетевые модели, графовые модели, отображаемые граф схемами.

г) Знаково-символьные модели: специальные методы кодирования сообщений, операторные схемы алгоритмов.

Все языки связаны, и их можно представить в следующем виде.

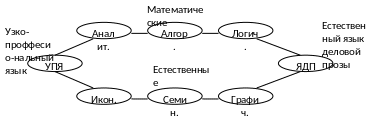
В соответствии с выбранным языком выбирается метод моделирования. Иногда в качестве исходного используется естественный язык, затем, на основе аппроксимации, переходя к математическим.

81. Иерархии языков описания в зависимости от этапов создания модели.

Абстрактные модели являются языковыми конструкциями. Абстрактные модели могут формироваться и передаваться другим людям средствами разных языков, языков разных уровней специализации. Во-первых, посредством естественного языка (как конечный результат, поскольку в процессе построения моделей человеком используются и неязыковые формы мышления – «интуиция», образное мышление и т.д.). На естественном языке человек может говорить обо всем, этот язык является средством построения любых абстрактных моделей. Универсальность естественного языка достигается еще и тем, что языковые модели обладают неоднородностью, расплывчатостью, размытостью. Многозначность почти каждого слова, используемого в естественном языке любой национальности, а также неопределенность слов (несколько, почти, много и т.д.) при огромном числе вариантов их соединения во фразы позволяет любую ситуацию отобразить с достаточной для обычных практических целей точностью. Эта приблизительность является неотъемлемым свойством языковых моделей. Но рано или поздно практика сталкивается с ситуациями, когда приблизительность естественного языка оборачивается недостатком, который необходимо преодолевать. Поэтому, во-вторых, для построения абстрактных моделей используются «профессиональные» языки. Их применяют люди, связанные общими для них, но частными для всех остальных людей, видами деятельности. Наиболее ярко это проявляется на примере языков конкретных отраслей наук сильной версии – физики, химии и др. Дифференциация наук объективно потребовала создания специализированных языков, более четких и точных, чем естественный. В-третьих, когда средств естественного и профессионального языков не хватает для построения моделей, используются искусственные, в том числе формализованные, языки – например, в логике, математике. К искусственным языкам также относятся компьютерные языки, чертежи, схемы и т.п. В результате получается иерархия языков и соответствующая иерархия типов моделей. На верхнем уровне этого спектра находятся модели, создаваемые средствами естественного языка, и так вплоть до моделей, имеющих максимально достижимую определенность и точность для сегодняшнего состояния данной отрасли профессиональной деятельности. Наверное, так и следует понимать известные высказывания И. Канта и К. Маркса о том, что любая отрасль знания может тем с большим основанием именоваться наукой, чем в большей степени в ней используется математика. Математические (в строгом смысле) модели обладают абсолютной точностью. Но чтобы дойти до их использования в какой-либо области, необходимо получить достаточный для этого объем достоверных знаний. Нематематизированность многих общественных и гуманитарных наук не означает их ненаучности, а есть следствие познавательной сложности их предметов. В них модели строятся, как правило, с использованием средств естественного языка.

82. Принципы перехода от морфологического описания к модели.

83. Диаграммная схема перехода от концептуального описания к концептуальной модели.

84. Структурно-функциональная модель и её анализ.

85. Примеры перехода от объекта к модели (апроксимационный подход).

86. Морфизмы модели и объекта.

Изоморфизм, эндоморфизм, автоморфизм

Морфизм   называется изоморфизмом, если существует такой морфизм  , что   и  . Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.

Морфизмы, в которых начало и конец совпадают, называют эндоморфизмами. Множество эндоморфизмов End(A) = Hom(A,A) является моноидом относительно операции композиции с единичным элементом id_A.

Эндоморфизмы, которые одновременно являются изоморфизмами, называются автоморфизмами. Автоморфизмы любого объекта образуют группу автоморфизмов Aut(A) по композиции.

Мономорфизм, эпиморфизм, биморфизм

Мономорфизм — это морфизм   такой, что для любых   из   следует, что g₁ = g₂. Композиция мономорфизмов есть мономорфизм.

Эпиморфизм — это такой морфизм, что для любых   из   следует g₁ = g₂.

Биморфизм — это морфизм, являющийся одновременно мономорфизмом и эпиморфизмом. Любой изоморфизм есть биморфизм, но не любой биморфизм есть изоморфизм.

Мономорфизм, эпиморфизм и биморфизм являются обобщениями понятий инъективного, сюръективного и биективного отображения соответственно. Любой изоморфизм является мономорфизмом и эпиморфизмом, обратное, вообще говоря, верно не для всех категорий.