Chapter 8
Literature, Software, Books and Websites
The yeoman work in any science…is done by the experimentalist, who must
keep the theoretician honest.
Michio Kaku, Professor of Theoretical Physics, City University of New York.
8.1FROM THE LITERATURE
A small smorgasbord of published papers will be discussed here, to show how some of the things that we have seen in previous chapters have appeared in the literature.
8.1.1 To be or not to be
8.1.1.1Oxirene
Let us start with what looks like a simple problem: what can computational chemistry tell us about oxirene (oxacyclopropene, Fig. 8.1; the oxirene literature till 1983 has been reviewed [1]). Labeling one of the carbons of a diazo ketone 
can lead to a ketene with scrambled labeling. After excluding the possibility of scrambling in the diazo compound, this indicates that an oxirene species is formed. However, this does not tell us whether this species is an intermediate or merely a transition state (Fig. 8.2). A straightforward way to try to answer this question would seem to be to calculate the frequencies, at the level used to optimize the structure, and see if there are any imaginary frequencies – a relative minimum has none, while a transition state has one (section 2.5). In a preliminary investigation [2] Schaefer and coworkers found that oxirene was a minimum with the Hartree-Fock (HF) (SCF) method, and also when electron correlation was taken into account (section 5.4) with the CISD and CCSD methods, using double-zeta basis sets (section 5.3). However, in going from HF to CISD to CCSD, the ring-opening frequency fell from 445 to 338 to 
which was said to be a much steeper drop than would be expected. A very comprehensive investigation with the above (“To be …”) title [3], in which the frequencies of oxirene were examined at 46 (!) different levels failed to definitively settle the matter: even using CCSD(T) calculations with large basis sets the results were somewhat quirky, and in fact of the six highest levels used, three gave an imaginary frequency and three
448 Computational Chemistry
Literature, Software, Books and Websites 449
all real frequencies. At the two highest levels the ring-opening frequency was real, but uncomfortably low (139 and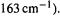 
Oxirene is the most notorious case of an unsolved computational “existence theorem”.
8.1.1.2Nitrogen pentafluoride
Nitrogen pentafluoride represents an interesting contrast to oxirene. Oxirene is, on paper, a reasonable molecule; there is no obvious reason why, however unstable it might be because of antiaromaticity [4] or strain, it should not be able to exist. On the other hand, 
defies the hallowed octet rule; why should it be more reasonable than, say, 
Yet a comprehensive computational study of this molecule left “little doubt” that it is a (relative) minimum on its potential energy surface [5]. The full armamentarium of post-HF methods, CASSDF, MRCI, CCSDT, CCSD(T), MP2 (section 5.4) and DFT (chapter 7) was employed here, and all agreed that 
(section 2.6)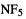 
is a minimum.
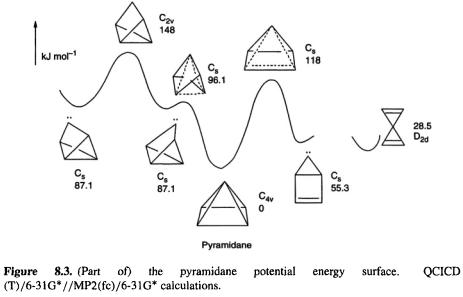
8.1.1.3 Pyramidane
If oxirene “should” exist and 
“should” not, what are we to make of pyramidane (Fig. 8.3)? This molecule contradicts the traditional paradigm [6] of tetracoordinate carbon having its bonds tetrahedrally directed: the four bonds of the apical carbon point toward the base of a pyramid. Part of the calculated [7] potential energy surface of pyramidane is shown in Fig. 8.3. To improve the accuracy of the relative energies, the MP2 geometries were subjected to single-point calculations (section 5.5.2) using the QCI method (section 5.4.3), with the results shown (Fig. 8.3). At the QCISD(T)/6-31G*//MP(fc)/6-31G* level pyramidane is predicted to be a relative