
- •COMPUTATIONAL CHEMISTRY
- •CONTENTS
- •PREFACE
- •1.1 WHAT YOU CAN DO WITH COMPUTATIONAL CHEMISTRY
- •1.2 THE TOOLS OF COMPUTATIONAL CHEMISTRY
- •1.3 PUTTING IT ALL TOGETHER
- •1.4 THE PHILOSOPHY OF COMPUTATIONAL CHEMISTRY
- •1.5 SUMMARY OF CHAPTER 1
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •2.1 PERSPECTIVE
- •2.2 STATIONARY POINTS
- •2.3 THE BORN–OPPENHEIMER APPROXIMATION
- •2.4 GEOMETRY OPTIMIZATION
- •2.6 SYMMETRY
- •2.7 SUMMARY OF CHAPTER 2
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •3.1 PERSPECTIVE
- •3.2 THE BASIC PRINCIPLES OF MM
- •3.2.1 Developing a forcefield
- •3.2.2 Parameterizing a forcefield
- •3.2.3 A calculation using our forcefield
- •3.3 EXAMPLES OF THE USE OF MM
- •3.3.2 Geometries and energies of polymers
- •3.3.3 Geometries and energies of transition states
- •3.3.4 MM in organic synthesis
- •3.3.5 Molecular dynamics and Monte Carlo simulations
- •3.4 GEOMETRIES CALCULATED BY MM
- •3.5 FREQUENCIES CALCULATED BY MM
- •3.6 STRENGTHS AND WEAKNESSES OF MM
- •3.6.1 Strengths
- •3.6.2 Weaknesses
- •3.7 SUMMARY OF CHAPTER 3
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •4.1 PERSPECTIVE
- •4.2.1 The origins of quantum theory: blackbody radiation and the photoelectric effect
- •4.2.2 Radioactivity
- •4.2.3 Relativity
- •4.2.4 The nuclear atom
- •4.2.5 The Bohr atom
- •4.2.6 The wave mechanical atom and the Schrödinger equation
- •4.3.1 Introduction
- •4.3.2 Hybridization
- •4.3.3 Matrices and determinants
- •4.3.4 The simple Hückel method – theory
- •4.3.5 The simple Hückel method – applications
- •4.3.6 Strengths and weaknesses of the SHM
- •4.4.1 Theory
- •4.4.2 An illustration of the EHM: the protonated helium molecule
- •4.4.3 The extended Hückel method – applications
- •4.4.4 Strengths and weaknesses of the EHM
- •4.5 SUMMARY OF CHAPTER 4
- •REFERENCES
- •EASIER QUESTIONS
- •5.1 PERSPECTIVE
- •5.2.1 Preliminaries
- •5.2.2 The Hartree SCF method
- •5.2.3 The HF equations
- •5.2.3.1 Slater determinants
- •5.2.3.2 Calculating the atomic or molecular energy
- •5.2.3.3 The variation theorem (variation principle)
- •5.2.3.4 Minimizing the energy; the HF equations
- •5.2.3.5 The meaning of the HF equations
- •5.2.3.6a Deriving the Roothaan–Hall equations
- •5.3 BASIS SETS
- •5.3.1 Introduction
- •5.3.2 Gaussian functions; basis set preliminaries; direct SCF
- •5.3.3 Types of basis sets and their uses
- •5.4 POST-HF CALCULATIONS: ELECTRON CORRELATION
- •5.4.1 Electron correlation
- •5.4.3 The configuration interaction approach to electron correlation
- •5.5.1 Geometries
- •5.5.2 Energies
- •5.5.2.1 Energies: Preliminaries
- •5.5.2.2 Energies: calculating quantities relevant to thermodynamics and to kinetics
- •5.5.2.2a Thermodynamics; “direct” methods, isodesmic reactions
- •5.5.2.2b Thermodynamics; high-accuracy calculations
- •5.5.2.3 Thermodynamics; calculating heats of formation
- •5.5.2.3a Kinetics; calculating reaction rates
- •5.5.2.3b Energies: concluding remarks
- •5.5.3 Frequencies
- •Dipole moments
- •Charges and bond orders
- •Electrostatic potential
- •Atoms-in-molecules
- •5.5.5 Miscellaneous properties – UV and NMR spectra, ionization energies, and electron affinities
- •5.5.6 Visualization
- •5.6 STRENGTHS AND WEAKNESSES OF AB INITIO CALCULATIONS
- •5.7 SUMMARY OF CHAPTER 5
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •6.1 PERSPECTIVE
- •6.2 THE BASIC PRINCIPLES OF SCF SE METHODS
- •6.2.1 Preliminaries
- •6.2.2 The Pariser-Parr-Pople (PPP) method
- •6.2.3 The complete neglect of differential overlap (CNDO) method
- •6.2.4 The intermediate neglect of differential overlap (INDO) method
- •6.2.5 The neglect of diatomic differential overlap (NDDO) method
- •6.2.5.2 Heats of formation from SE electronic energies
- •6.2.5.3 MNDO
- •6.2.5.7 Inclusion of d orbitals: MNDO/d and PM3t; explicit electron correlation: MNDOC
- •6.3 APPLICATIONS OF SE METHODS
- •6.3.1 Geometries
- •6.3.2 Energies
- •6.3.2.1 Energies: preliminaries
- •6.3.2.2 Energies: calculating quantities relevant to thermodynamics and kinetics
- •6.3.3 Frequencies
- •6.3.4 Properties arising from electron distribution: dipole moments, charges, bond orders
- •6.3.5 Miscellaneous properties – UV spectra, ionization energies, and electron affinities
- •6.3.6 Visualization
- •6.3.7 Some general remarks
- •6.4 STRENGTHS AND WEAKNESSES OF SE METHODS
- •6.5 SUMMARY OF CHAPTER 6
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •7.1 PERSPECTIVE
- •7.2 THE BASIC PRINCIPLES OF DENSITY FUNCTIONAL THEORY
- •7.2.1 Preliminaries
- •7.2.2 Forerunners to current DFT methods
- •7.2.3.1 Functionals: The Hohenberg–Kohn theorems
- •7.2.3.2 The Kohn–Sham energy and the KS equations
- •7.2.3.3 Solving the KS equations
- •7.2.3.4a The local density approximation (LDA)
- •7.2.3.4b The local spin density approximation (LSDA)
- •7.2.3.4c Gradient-corrected functionals and hybrid functionals
- •7.3 APPLICATIONS OF DENSITY FUNCTIONAL THEORY
- •7.3.1 Geometries
- •7.3.2 Energies
- •7.3.2.1 Energies: preliminaries
- •7.3.2.2 Energies: calculating quantities relevant to thermodynamics and kinetics
- •7.3.2.2a Thermodynamics
- •7.3.2.2b Kinetics
- •7.3.3 Frequencies
- •7.3.6 Visualization
- •7.4 STRENGTHS AND WEAKNESSES OF DFT
- •7.5 SUMMARY OF CHAPTER 7
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •8.1 FROM THE LITERATURE
- •8.1.1.1 Oxirene
- •8.1.1.2 Nitrogen pentafluoride
- •8.1.1.3 Pyramidane
- •8.1.1.4 Beyond dinitrogen
- •8.1.2 Mechanisms
- •8.1.2.1 The Diels–Alder reaction
- •8.1.2.2 Abstraction of H from amino acids by the OH radical
- •8.1.3 Concepts
- •8.1.3.1 Resonance vs. inductive effects
- •8.1.3.2 Homoaromaticity
- •8.2 TO THE LITERATURE
- •8.2.1 Books
- •8.2.2 The Worldwide Web
- •8.3 SOFTWARE AND HARDWARE
- •8.3.1 Software
- •8.3.2 Hardware
- •8.3.3 Postscript
- •REFERENCES
- •INDEX

Ab initio calculations 297
requires a knowledge of the shapes of the drug and of the active site [82]). The relative energies of molecular species is fundamental to a knowledge of their kinetic and thermodynamic behaviour, and this can be important in attempts to synthesize them. The vibrational frequencies of a molecule, provide information about the electronic nature of its bonds, and prediction of the spectra represented by these frequencies may be useful to experimentalists.
A fourth important characteristic of a molecule is the distribution ofelectron density in it. Calculation of the electron density distribution enables one to predict the dipole moment, the charge distribution, the bond orders, and the shapes of various molecular orbitals.
Dipole moments
The dipole moment [ 161 ] of a system of two charges Q and – Q separated by a distance  is, by definition, the vector Qr ; the direction of the vector is officially from – Q toward +Q, but chemists usually assign a molecular or bond dipole (see below) the direction from the positive end of the bond or molecule to the negative (Fig. 5.37(a)). The dipole moment of a collection of charges with corresponding
is, by definition, the vector Qr ; the direction of the vector is officially from – Q toward +Q, but chemists usually assign a molecular or bond dipole (see below) the direction from the positive end of the bond or molecule to the negative (Fig. 5.37(a)). The dipole moment of a collection of charges with corresponding
position vectors (Fig. 5.37(b)) is
(Fig. 5.37(b)) is
and the so the dipole moment of a molecule is seen to arise from the charges and positions of its component electrons and nuclei. The dipole moment of a molecule is an experimental observable [162], with which we can compare calculated moments. It is often convenient to think of the molecular dipole moment as the vector sum of bond moments (Fig. 5.37(c)). Two points should be noted: we are discussing an average dipole moment, because electron and nuclear motions will cause the dipole moment to fluctuate, so that even a spherical atom can have temporary nonzero dipole moments. Another point is that we usually consider the dipole moments of neutral molecules only, not of ions; this is because the dipole moment of a charged species is not unique, but depends on the choice of the point in the coordinate system from which the position vectors are measured.
Let us look at the calculation of the dipole moment within the HF approximation. The quantum mechanical analogue of Eq. (5.200) for the electrons in a molecule is
Here the summation of charges times position vectors is replaced by the integral over thetotalwavefunction  (the square of the wavefunction is a measure of charge) of the dipole moment operator (the summation over all electrons of the product of an electronic charge and the position vectors of the electrons). To perform an ab initio calculation of the dipole moment of a molecule we want an expression for the moment in terms of the basis functions
(the square of the wavefunction is a measure of charge) of the dipole moment operator (the summation over all electrons of the product of an electronic charge and the position vectors of the electrons). To perform an ab initio calculation of the dipole moment of a molecule we want an expression for the moment in terms of the basis functions their coefficients
their coefficients and the geometry (for a molecule of specified charge and multiplicity these are the only “variables” in an ab initio calculation). The HF
and the geometry (for a molecule of specified charge and multiplicity these are the only “variables” in an ab initio calculation). The HF

298 Computational Chemistry
totalwavefunction is composed of those component orbitals
is composed of those component orbitals  which are occupied, assembled into a Slater determinant (section 5.2.3.1), and the
which are occupied, assembled into a Slater determinant (section 5.2.3.1), and the  are composed of basis functions and their coefficients (sections 5.3). Eq. (5.201), with the inclusion of the contribution of the nuclei to the dipole moment, leads to the dipole moment in Debyes as ([1g], p. 41)
are composed of basis functions and their coefficients (sections 5.3). Eq. (5.201), with the inclusion of the contribution of the nuclei to the dipole moment, leads to the dipole moment in Debyes as ([1g], p. 41)
Ab initio calculations 299
Here the first term refers to the nuclear charges and position vectors and the second term (the double summation) refers to the electrons.  = the density matrix elements (sections 5.2.3.6d and 5.2.3.6e), cf.:
= the density matrix elements (sections 5.2.3.6d and 5.2.3.6e), cf.:
The P summation is over the occupied orbitals ( j = 1,2,..., n; we are considering closed-shell systems, so there are 2n electrons) and the double summation is over the m basis functions. The operator r is the electronic position vector.
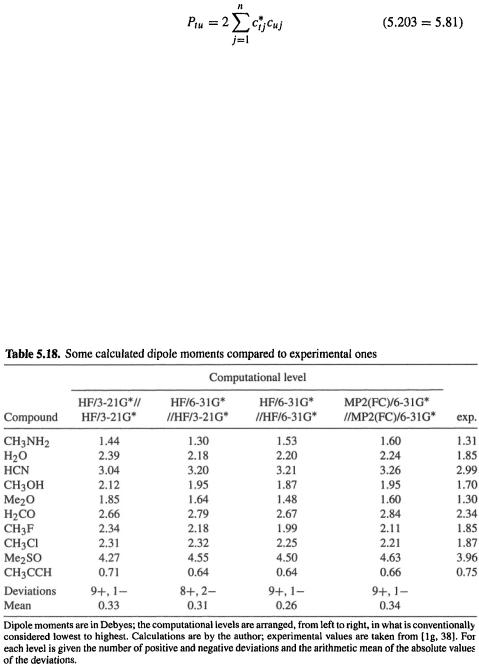
How good are ab initio dipole moments? Hehre’s extensive survey of practical ab initio methods [32] indicates that fairly good results are given by HF/6-31G*//HF/6-31G* (dipole moment from a HF/6-31G* calculation on a HF/6-31G* geometry) calculations, and that MP2/6-31G*//MP2/6-31G* calculations are usually not much better. Some calculated and experimental dipole moments are compared in Table 5.18. These results, which are quite typical, indicate that calculated values tend to be about 0.0–0.5 D higher than experimental, with a mean deviation of about 0.3 D; negative deviations are rare. HF/3-21G//HF/3-21G (the lowest ab initio level likely to be used) calculations may show the largest deviations. Single-point HF/6-31G* calculations on HF/3-21G geometries appear to give results about as good as (or better than? Note  and [32], pp. 76, 77) those from MP2(FC)/6-31G*//MP2(FC)/6-31G* calculations. As is the case for other properties, 3-21G calculations of dipole moments on molecules with atoms beyond neon require
and [32], pp. 76, 77) those from MP2(FC)/6-31G*//MP2(FC)/6-31G* calculations. As is the case for other properties, 3-21G calculations of dipole moments on molecules with atoms beyond neon require

300 Computational Chemistry
polarization functions for reasonable results (the 3-21G(*) basis; [32], pp. 23–30). The 3-21G* calculations in Table 5.18 show a mean deviation 0.33; the HF/6-31G* calculations are only slightly better (mean deviation 0.26) and the MP2/6-31G* calculations appear to be, if anything, slightly worse (mean error 0.34). If high-accuracy calculated dipole moments (0.1 D or better) are needed, high-level correlation and large basis sets must be used; such calculations may be needed to reproduce the magnitude and even the direction of small dipole moments, e.g. in carbon monoxide [163].
Charges and bond orders
Chemists make extensive use of the idea that the atoms in a molecule can be assigned electrical charges. Thus in a water molecule each hydrogen atom is considered to have an equal, positive, charge, and the oxygen atom to have a negative charge (equal in magnitude to the sum of the hydrogen charges). This concept is clearly related to the dipole moment: in a diatomic (for simplicity) molecule one expects the negative end of the dipole vector to point toward the atom assigned the negative charge. However, there are two problems with the concept: first, the charge on an atom in a molecule, unlike the dipole moment of a molecule, cannot be measured (it is not an observable). Second, there is no unique, correct theoretical method for calculating the charge on an atom in a molecule.
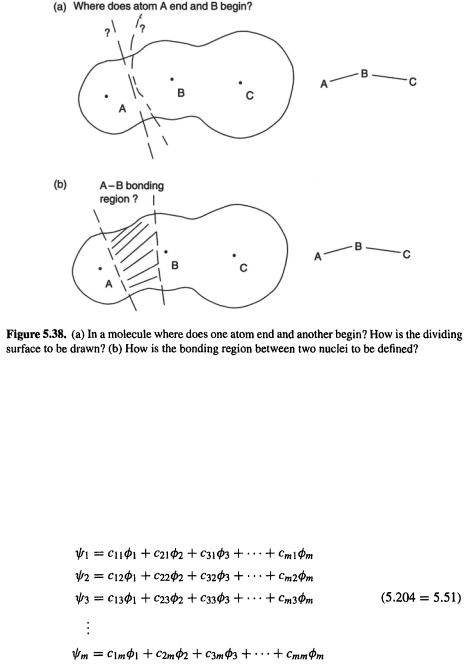
Both the measurement and calculational problems arise from the difficulty of defining what we mean by “an atom in a molecule”. Consider the hydrogen chloride molecule. As we move from the hydrogen nucleus to the chlorine nucleus, where does the hydrogen atom end and the chlorine atom begin? If we had a scheme for partitioning the molecule into atoms (Fig. 5.38(a)), the charge on each atom could be defined as the net electric charge within the space of the atom, i.e. the algebraic sum of the electronic and the nuclear charges. The electronic charge in the defined space could be found by integrating the electron density (essentially the square of the wavefunction; only the wavefunction composed of the occupied orbitals need be considered) over that region of space.
Bondorder is a term with conceptual difficulties related to those associated with atom charges. The simplest electronic interpretation of a bond is that it is a pair of electrons shared between two nuclei, somehow [164] holding them together. From this criterion and Lewis structures the C/C bond order in ethane is 1, in ethene 2, and in ethyne 3, in accordance with the classical assignment of a single, a double, and a triple bond, respectively. However, if a bond is a manifestation of the electron density between two
nuclei, then the bond order need not be an integer; thus the |
|
bond in |
might be expected to have a lower bond order than the |
in |
because |
the  group might drain electron density away toward the electronegative oxygen. However, an attempt to calculate bond order from electron density (the square of the wavefunction) runs into the problem that in a polyatomic molecule, at any rate, it is not clear how to define precisely the region “between” two atomic nuclei (Fig. 5.38(b)).
group might drain electron density away toward the electronegative oxygen. However, an attempt to calculate bond order from electron density (the square of the wavefunction) runs into the problem that in a polyatomic molecule, at any rate, it is not clear how to define precisely the region “between” two atomic nuclei (Fig. 5.38(b)).
Assigning atom charges and bond orders involves calculating the number of electrons “belonging to” an atom or shared “between” two atoms, i.e. the “population” of electrons on or between atoms; hence such calculations are said to involve population analysis. Earlier schemes for population analysis bypassed the problem of defining the space occupied by atoms in molecules, and the space occupied by bonding electrons, by partitioning electron density in a somewhat arbitrary way. The earliest such schemes
Ab initio calculations 301
were utilized in the simple Hückel or similar methods [165], and related these quantities to the basis functions (which in these methods are essentially valence, or even just p, atomic orbitals; see section 4.3.4). The simplest scheme used in ab initio calculations is Mulliken population analysis [166].
Mulliken population analysis is in the general spirit of the scheme used in the simple Hückel method, but allows for several basis functions on an atom and does not require the overlap matrix to be a unit matrix. In ab initio theory each molecular orbital has a wavefunction (section 5.2.3.6a):
(section 5.2.3.6a):
Here the basis set  engenders MOs
engenders MOs 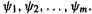 Several basis functions can reside on each atom, so
Several basis functions can reside on each atom, so  is the coefficient of basis function s (not, as in simple Hückel theory, atom s) in MO i. For any MO
is the coefficient of basis function s (not, as in simple Hückel theory, atom s) in MO i. For any MO  squaring and integrating
squaring and integrating

302 Computational Chemistry
over all space gives
The integral equals one because the probability that the electron is somewhere in the MO (which, strictly, extends over all space) is one; the  (both
(both  the same) overlap integrals are also unity, since the basis functions are normalized (cf. section 4.4.1 b).
the same) overlap integrals are also unity, since the basis functions are normalized (cf. section 4.4.1 b).
In the Mulliken scheme each electron in |
is taken to contribute a “fraction of an |
|||
electron” |
|
to basisfunction |
and a fraction of an electron |
|
(see Eq. (5.205)) |
to the |
overlap region, |
and in general to contribute a fraction |
|
of an electron |
to the basis function (“orbital”) |
and a fraction of an electron |
||
to the |
|
overlap space; see Fig. 5.39(a). This seems reasonable since |
||
(1), the terms sum to one (the “fractions” of the electron must add to one), and (2) it seems reasonable to partition the contribution of electrons to basis functions and overlap regions according to the “electron density sum” in Eq. (5.205). Now if there
are |
electrons |
in MO |
then the contributions of |
to the electron population of |
|
basis function |
and of the overlap region between |
and |
are |
||
and
The total contributions from all the MOs to the electron population in  and in the overlap region between
and in the overlap region between  and
and  are
are
and
The sums are over the occupied MOs, since |
for the virtual MOs. The number |
|||||||
is the Mulliken net population in the basis function |
and the number |
is the |
||||||
Mulliken overlap population for the pair of basis functions |
and |
The net population |
||||||
summed over all |
plus the overlap population summed over all |
pairs equals the |
||||||
total number of electrons in the molecule. |
|
|
|
|
||||
The quantities |
and |
|
are used to calculate atom charges and bond orders. The |
|||||
Mulliken gross population in the basis function |
is defined as the Mulliken net pop- |
|||||||
ulation |
(Eq. (5.206)) plus one half of all those Mulliken overlap populations |
|
||||||
(Eq. (5.207)) which involve |
(of course for some |
|
may be negligible; e.g. for |
|||||
well-separated atoms |
is very small): |
|
|
|
|
|||

Ab initio calculations 303
The gross population |
is an attempt to represent the total electron population in the |
||||||
basis function |
; this is considered here to be the net population |
the population |
|||||
that all the occupied MOs contribute to |
through the representation of |
in each |
|||||
by its coefficient |
(Eq. (5.208), plus one-half of the all the populations in the overlap |
||||||
regions involving |
|
(Fig. 5.39(b)). Assigning to |
one-half, rather than some other |
||||
fraction, of the electron population in an overlap region with |
is said to be arbitrary. |
||||||
Of course it is not arbitrary, in the sense that Mulliken thought about it carefully and decided that one-half was at least as good as any other fraction. One might imagine a more elaborate partitioning in which the fraction depends on the electronegativity difference between the atoms on which and
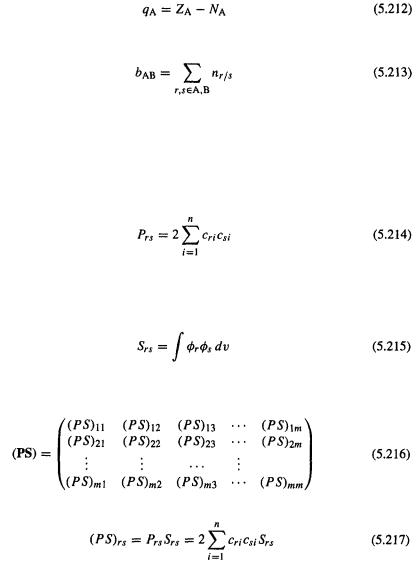
and  reside, with the more electronegative atom getting the larger share of the electron population. To get the charge on an atom A we calculate the gross atomic population for A:
reside, with the more electronegative atom getting the larger share of the electron population. To get the charge on an atom A we calculate the gross atomic population for A:
304 Computational Chemistry
This is the sum over all the basis functions  on atom A
on atom A  A qualifying the summation means “r belonging to A”) of the gross populations in each
A qualifying the summation means “r belonging to A”) of the gross populations in each (Eq. (5.210); it involves all the basis functions on A and all the overlap regions these functions have with other basis functions
(Eq. (5.210); it involves all the basis functions on A and all the overlap regions these functions have with other basis functions We can regard
We can regard  as the total electron population on atom A (within the limits of the Mulliken treatment). The Mulliken charge on atom A, the net charge on A, is then simply the algebraic sum of the charges due to the electrons and the nucleus:
as the total electron population on atom A (within the limits of the Mulliken treatment). The Mulliken charge on atom A, the net charge on A, is then simply the algebraic sum of the charges due to the electrons and the nucleus:
The Mulliken bond order for the bond between atoms A and B is the total population for the A/B overlap region:
The overlap population for basis functions  and
and 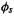 (Eq. (5.209)) is summed over all the overlaps between basis functions on atoms A and B.
(Eq. (5.209)) is summed over all the overlaps between basis functions on atoms A and B.
Since the formulas for calculating Mulliken charges and bond orders (Eqs (5.206)- (5.213)) involve summing basis function coefficients and overlap integrals, it is not too surprising that they can be expressed neatly in terms of the density matrix (section 5.2.3.6d) P and the overlap matrix S (section 4.3.3). The elements of the density matrix P are
The matrix element  is summed over all filled MOs (from
is summed over all filled MOs (from  to
to  for the ground electronic state of a 2n-electron closed-shell molecule); an example of the calculation of P was given in section 5.2.3.6e. The elements of the overlap matrix S are simply the overlap integrals:
for the ground electronic state of a 2n-electron closed-shell molecule); an example of the calculation of P was given in section 5.2.3.6e. The elements of the overlap matrix S are simply the overlap integrals:
From Eq. (5.214) it follows that the matrix (PS) obtained by multiplying corresponding elements of P and S,
has elements
Note that (PS) is not the matrix PS obtained by matrix multiplication of P and S; each element of that matrix would result from series multiplication: a row of P times a column of S (section 4.3.3).

Ab initio calculations 305
The diagonal elements of (PS) are
Compare this with Eq. (5.208): for a ground-state closed-shell molecule there are 2 electrons in each occupied MO and Eq. (5.208) can be written as:
i.e.
The off-diagonal elements of (PS) are given by Eq. (5.217), 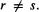 Compare this with Eq. (5.209): for a ground-state closed-shell molecule there are 2 electrons in each occupied MO and Eq. (5.209) can be written as:
Compare this with Eq. (5.209): for a ground-state closed-shell molecule there are 2 electrons in each occupied MO and Eq. (5.209) can be written as:
i.e.
Thus the matrix (PS) can be written as:
The matrix (PS) (or sometimes 2(PS)) is called a population matrix.
An example of population analysis: 
As a simple illustration of the calculation of atom charges and bond orders, consider  From our HF calculations on this molecule (section 5.2.3.6e) we have
From our HF calculations on this molecule (section 5.2.3.6e) we have
Therefore,
From Eq. (5.223), (PS) gives us

306 Computational Chemistry
Charge on H,  For this we need
For this we need  the sum of all the
the sum of all the  on H (Eqs (5.211) and (5.210)). There is only one basis function on H,
on H (Eqs (5.211) and (5.210)). There is only one basis function on H,  so there is only one relevant
so there is only one relevant  for H, and for
for H, and for there is only one overlap, with
there is only one overlap, with 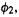 so the summation involves only one term,
so the summation involves only one term,  Using Eq. (5.210):
Using Eq. (5.210):
The sum of all the  on H has only one term,
on H has only one term,  since there is only one basis function on H. Using Eq. (5.211):
since there is only one basis function on H. Using Eq. (5.211):
The charge on H, 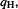 is the algebraic sum of the gross electronic population and the nuclear charge (Eq. (5.212)):
is the algebraic sum of the gross electronic population and the nuclear charge (Eq. (5.212)):
Charge on He, 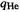 For this we need
For this we need  There is only one basis function on He,
There is only one basis function on He,  for
for  there is only one overlap, with
there is only one overlap, with 
the sum of all the  on He (Eq. (5.211). so there is only one relevant
on He (Eq. (5.211). so there is only one relevant  for He, and so the summation involves only one term,
for He, and so the summation involves only one term,
The sum of all the 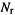 on He has only one term,
on He has only one term,  since there is only one basis function on He:
since there is only one basis function on He:
The charge on He,  is the algebraic sum of the gross electronic population and the nuclear charge:
is the algebraic sum of the gross electronic population and the nuclear charge:
The charges sum to 0.5423 + 0.4579 = 1.000, the total charge on the molecule. The less positive charge on helium is in accord with the fact that electronegativity increases from left to right along a row of the periodic table. H–He bond order For this we use Eq. (5.213);  is summed for all overlaps between basis functions on atoms A and B. There is only one such overlap, that between
is summed for all overlaps between basis functions on atoms A and B. There is only one such overlap, that between  and
and  so
so
Note that the elements of the population matrix (PS) sum to the number of electrons in the molecule: 0.2020 + 1.2864 + 0.2557 + 0.2557 = 2.000. This is expected, since
