262 Computational Chemistry

FOO angle, 107.5° (–2.0)

FOOF dihedral, 86.7° (–0.8)

OO length, 1.296 Å (0.024)

OOO angle, 116.5° (–0.3)

The geometry is now on the verge of satisfying ours “accurate” requirement, but the FOOF geometry still has unsatisfactory bond lengths. CCSD(T) with a considerably bigger basis set (similar to 6-311 (2d)) has been reported [92] to give for FOOF errors of 0.039, –0.001, –0.6 and 0.3 for the FO and OO lengths and the FOO angle and FOOF dihedral, respectively; even here one of the bond lengths does not meet the “accurate” criterion of being within 0.02 Å of experiment.

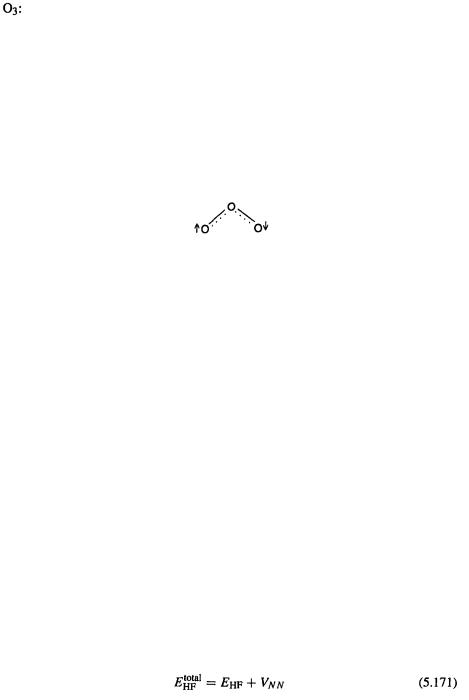
The problem with ozone probably arises at least partly from the fact that this molecule has singlet diradical character: it is approximately a species in which two electrons, although having opposite spin, are not paired in the same orbital:

The HF method works best with normal closed-shell molecules, because it uses a single Slater determinant, but ozone has open-shell diradical character: it is, or at least resembles, a species with two half-filled orbitals, one with a single α electron and the other with a single electron; there are various ways of handling this molecule [91]. The cause of the problems with FOOF are harder to explain, but fluorine is known to be a somewhat troublesome element [92], although not all fluorine-containing species require very large basis sets [93].

5.5.2 Energies

5.5.2.1 Energies: Preliminaries

Along with geometries (section 5.5.1), the molecular features most frequently sought from ab initio calculations are probably energies. An ab initio calculation gives an energy quantity that represents the energy of the molecule (or atom) relative to its stationary constituent electrons and nuclei at infinite separation, this separated state being taken as the zero of energy. The ab initio energy of a species is thus the negative of the energy needed to dissociate it completely (to infinite separation) into the electrons and nuclei, or the negative of the energy given out when the electrons and nuclei “fall together” from infinity to form the species. This was pointed out for HF energies (section 5.2.3.6d, in connection with Eq. (5.93)), and the infinite-separation reference point also holds for correlated ab initio energies. By ab initio energy, then, we normally mean the electronic energy (whether calculated by the HF or by a correlation method) plus the internuclear repulsion (cf. Eq. (5.93):

ab initio energy (Hartree–Fock):

Ab initio calculations 263

ab initio energy (correlated method):

If the ab initio energy has been corrected by adding the ZPE (cf. Eq. (5.94)), giving the total internal energy at 0 K, this should be pointed out: ab initio energy, corrected for ZPE:

The ZPE-corrected ab initio energy is preferred for calculating relative energies (see

What we actually want is usually not these “absolute” ab initio energies, because chemistry really deals with relative energies (all energies are relative to something, but in this context it is useful to restrict the term to the energy difference between reactants and products or transition states, or between two isomers). We are thus interested in the reaction energy (the energy difference between the product and reactant) and what we might call the activation energy (the energy difference between the transition state and reactant; note however – see below – that the well-known Arrhenius activation energy is not simply the difference in calculated energies of transition state and reactants). Calculating the relative stabilities of isomers amounts to calculating the reaction energy of an isomerization reaction.

Figure 5.24 shows what Coulson meant when he said that calculating the relative stabilities of isomers by subtracting absolute energies is like finding the weight of the captain by weighing the ship with and without him [94]. The absolute ab initio energies

typical. If we conservatively assign a captain a weight of 100kg, the analogy corresponds to a small ship weighing 4,500,000 kg or about 5000 tonnes. Yet the astonishing thing is that modern ab initio calculations can, as we shall see, accurately and reliably predict relative energies. A comprehensive account of energy calculations by ab initio and other methods is given by Irikura and Frurip [95].

Reaction energies belong to the realm of thermodynamics, and activation energies to that of kinetics: the energy difference between the products and the reactants (“difference” is defined here as product energy minus reactant energy) determines the extent to which a reaction has progressed at equilibrium, i.e the equilibrium constant, and the energy difference between the transition state and the reactants (transition state energy minus reactant energy) determines (partially; see section 5.5.2.2d) the rate of the reaction, i.e the rate constant (Fig. 5.25). The term “energy” in chemistry can mean (to give the three most common entities) potential energy, enthalpy (heat content), H, or Gibbs free energy, G. The potential energy on a computed Born–Oppenheimer surface (the usual “potential energy surface”; section 2.3) represents 0 K enthalpy differences

264 Computational Chemistry

Ab initio calculations 265

More detailed discussion of enthalpy, free energy, and entropy are given in books on thermodynamics, and the relationships between these quantities and processes at the molecular level are explained in books on statistical mechanics [96]; general discussions of these topics are given in physical chemistry texts [97].

To get an intuitive feel for we can regard it as essentially a measure of the strengths of the bonds in the products or the transition state, compared to the strengths of the bonds in the reactants [98]:

(pdt or TS depending on whether we are considering reaction enthalpy or activation enthalpy). Thus an exothermic process, which from the definition has has stronger bonds in the products than in the reactants; in some sense the bonds lose heat energy, becoming tighter and stabler. The bond energy tables given in most organic chemistry textbooks can be used to calculate rough values of (reaction), and accurate reaction enthalpies can sometimes be obtained from the more sophisticated use of bond energies and similar quantities [99]. To see an application of simple bond energy tables [100], consider the keto/enol reaction:

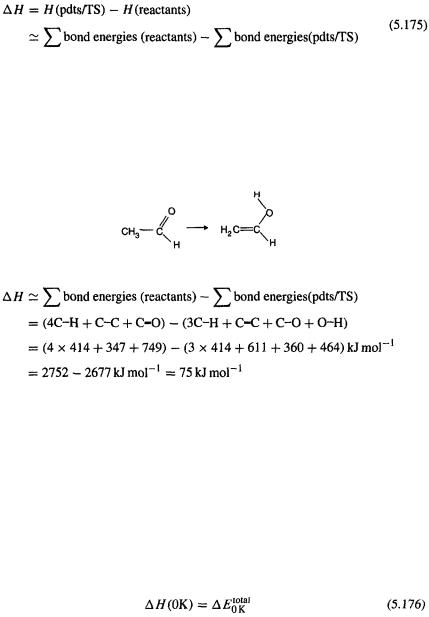
Using Eq. (5.175):

The ethanal to ethenol (acetaldehyde to vinyl alcohol) reaction is predicted to be endothertnic by i.e. neglecting entropy the enol is predicted to lie above the aldehyde. Because these are only average bond energies, the apparently remarkable agreement with the ab initio calculations in Fig. 5.21 the connection between from calculations like this and from ab initio calculations is discussed below) must be regarded as a coincidence. In any case, the correct value is about (section 5.5.2.2e). Crude bond energy calculations like this can be expected to be in error by 50 or more Accurate bond energy calculations can however be done [99] using essentially bond energies that refer to quite specific structural environments; for example, a C–H bond on a primary carbon that is in turn attached to another carbon.

For a reaction taking place at 0 K the enthalpy change is simply the internal energy change at 0 K:

266 Computational Chemistry

Note that although the calculation of values for demands frequency jobs, which are relatively time-consuming (“expensive”), accurate relative energy differences require this, and we will regard the ZPE-uncorrected ab initio energy as only an approximation to (see 5.2.3.6d and Fig. 2.20). At temperatures other than 0 K, is plus the increases in translational, rotational, vibrational and electronic energies on going from 0 K to the higher temperature T, plus the work done by the system in effecting a pressure or volume change:

One frequently chooses the standard temperature of 298.15 K, about room temperature. From 0 K to room temperature the increase in electronic energy is negligible and the increase in vibrational energy is small.

The entropy difference for a process is essentially a measure of the disorder of the products or the transition state, compared to the disorder of the reactants:

(pdt or TS depending on whether we are considering reaction entropy or activation entropy)

Entropy is a sophisticated concept, and this is not the place to give a rigorous definition of disorder; suffice it to say that a disordered system is more probable than an ordered one, and the entropy ofa system is proportional to the logarithm of its probability [101]. Intuitively, we see that for a process in which the product or the transition state is less symmetrical or has more freedom of motion than do the reactants. For example, ring-opening reactions, since they relieve constraints on intramolecular motion, should be accompanied by an increase in entropy. Note that an increase in entropy favors a process: it increases a rate constant (activation entropy) or an equilibrium constant (reaction entropy), while an increase in enthalpy disfavors a process.

More details on the calculation of entropies is given in the book by Hehre, Radom, Schleyer and Pople, who also tabulate the errors in calculated entropy for small molecules composed of elements from H to F [102]. Errors in calculated entropies at

for frequency calculations at the HF/3-21G, 6-31G* and MP2/6-31G* levels, respec-

be reliably obtained with high-accuracy methods (see below) and shows that in current ab initio work errors in free energies can be expected to come mainly from the enthalpy. Many programs, e.g. Gaussian and Spartan, automatically calculate the correction terms to be added to in Eq. (5.177) at the end of a frequency calculation, and print out the 298.15K enthalpy or the correction to the 0 K enthalpy. Reaction entropies are needed to calculate free energies of reaction (from Eq. (5.174)), from which equilibrium constants [103] can be calculated:

Ab initio calculations 267

where several species are in equilibrium, the ratios are proportional to their Boltzmann exponential factors. For example, if the relative free energies G of A, B and C are 0, 5.0 and (here G for A has been set to zero and B and C lie 5.0 and higher) then

at room temperature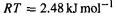 and so at this temperature

Activation entropies are useful because they can give information on the structure of a transition state (as stated above, a more confined transition state is signalled by a negative activation entropy), but the ab initio calculation of rate constants [104] from activation free energies is not as straightforward as the calculation of equilibrium constants from reaction free energies. The crudest way to calculate a rate constant is to use the Arrhenius equation [96c,105]

and to simply approximate the preexponential factor A by that for a similar reaction (a typical value is [106])and to approximate 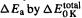or by the value of (the activation enthalpy) at the temperature in question. The Arrhenius activation energy and the activation enthalpy are actually related by

for a unimolecular reaction, and by

for a bimolecular reaction in the gas phase [107]. The main problem with this is that the preexponential factor A varies by a large factor even for, say, reactions which are formally unimolecular [106]:

so that this method of guessing by analogy could give a value for of A that was out by a

to within a factor of 100 would be very useful for estimating the stability of unknown substances. Note that for unimolecular processes like the rearrangement of a molecule to a stabler isomer, the halflife, an intuitively more meaningful quantity than the rate constant, is simply

i.e. the halflife of a unimolecular reaction is approximately the reciprocal of its rate constant.