Introduction to Quantum Mechanics 151

0.85 Å for ethane, ethene and ethyne, respectively, cf. the actual values of 1.53, 1.33 and 1.21 Å, and although the favored conformation of an alkane is usually correctly identified, the energy barriers and differences are generally at best in only modest agreement with experiment. Because of this inability to reliably calculate geometries, EHM calculations are usually not used for geometry optimizations, but rather utilize experimental geometries.

4.5 SUMMARY OF CHAPTER 4

This chapter introduces the application of quantum mechanics (QM) to computational chemistry by outlining the development of QM up to the Schrödinger equation and then showing how this equation led to the SHM, from which the EHM followed.

Quantum mechanics teaches, basically, that energy is quantized: absorbed and emitted in discrete packets (quanta) of magnitude hv, where h is Planck’s constant and v (Greek nu) is the frequency associated with the energy. QM grew out of studies of blackbody radiation and of the photoelectric effect. Besides QM, radioactivity and relativity contributed to the transition from classical to modern physics. The classical Rutherford nuclear atom suffered from the deficiency that Maxwell’s electromagnetic theory demanded that its orbiting electrons radiate away energy and swiftly fall into the nucleus. This problem was countered by Bohr’s quantum atom, in which an electron could orbit stably if its angular momentum was an integral multiple of However, the Bohr model contained several ad hoc fixes and worked only for the hydrogen atom. The deficiencies of the Bohr atom were surmounted by Schrödinger’s wave mechanical atom; this was based on a combination of classical wave theory and the de Broglie postulate that any particle is associated with a wavelength where p is the momentum. The four quantum numbers follow naturally from the wave mechanical treatment and the model does not break down for atoms beyond hydrogen.

Hückel was the first to apply QM to species significantly more complex than the hydrogen atom. The Hückel approach is treated nowadays within the framework of the concept of hybridization: the electrons in p orbitals are taken into account and the electrons in an framework are ignored. Hybridization is a purely mathematical convenience, a procedure in which atomic (or molecular) orbitals are combined to give new orbitals; it is analogous to the combination of simple vectors to give new vectors (an orbital is actually a kind of vector).

The SHM (SHT, HMO method) starts with the Schrödinger equation in the form where 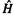is a Hamiltonian operator, is a MO wavefunction and E is the energy of the system (atom or molecule). By expressing as a LCAO and minimizing E with respect to the LCAO coefficients one obtains a set of simultaneous equations, the secular equations. These are equivalent to a single matrix equation,

H is an energy matrix, the Fock matrix, C is the matrix of the LCAO coefficients, S is the overlap matrix and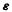 is a diagonal matrix whose nonzero, i.e. diagonal, elements are the MO energy levels. The columns of C are called eigenvectors and the diagonal

152 Computational Chemistry

LCAO, and the MO energies. To get numbers for H the SHM reduces all the Fock matrix elements to (the coulomb integral, for AOs on the same atom) and (the bond integral or resonance integral, for AOs not on the same atom; for nonadjacent atoms is 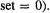To get actual numbers for the Fock elements, and are defined as energies relative to in units of this makes the Fock matrix consist ofjust 0s and

– 1s, where the 0s represent same-atom interactions and nonadjacent-atom interactions, and the –1s represent adjacent-atom interactions. The use of just two Fock elements is a big approximation. The SHM Fock matrix is easily written down just by looking at the way the atoms in the molecule are connected. Applications of the SHM include predicting:

(a)The nodal properties of the MOs, very useful in applying the Woodward–Hoffmann rules.

(b)The stability of a molecule based on its filled and empty MOs, and its delocalization

energy or resonance energy, based on a comparison of its total withthat of a reference system. The pattern of filled and empty MOs led to Hückel’s rule (the 4n + 2 rule) which says that planar molecules with completely conjugated p orbitals containing 4n + 2 electrons should be aromatic.

(c)Bond orders and atom charges, which are calculated from the AO coefficients of the occupied MOs (in the SHM LCAO treatment, p AOs are basis functions that make up the MOs).

The strengths of the SHM lie in the qualitative insights it gives into the effect of molecular structure on orbitals. Its main triumph in this regard was its spectacularly successful prediction of the requirements for aromaticity (the Hückel 4n + 2 rule).

The weaknesses of the SHM arise from the fact that it treatsonly electrons(limiting its applicability largely to planar arrays), its all-or-nothing treatment of overlap integrals, the use of just two values for the Fock integrals, and its neglect of electron spin and interelectronic repulsion. Because of these approximations it is not used for geometry optimizations and its quantitative predictions are sometimes viewed with suspicion. For obtaining eigenvectors and eigenvalues from the secular equations an older and inelegant alternative to matrix diagonalization is the use of determinants.

The EHM (EHT) follows from the SHM by using a basis set that consists not just of p orbitals, but rather of all the valence AOs (a minimal valence basis set), by calculating (albeit very empirically) the Fock matrix integrals, and by explicitly calculating the overlap matrix S (whose elements are also used in calculating the Fock integrals). Because S is not taken as a unit matrix, the equation must be transformed to one without S before matrix diagonalization can be applied. This is done by a matrix multiplication

process called orthogonalization, involving which converts the original Fock matrix H, based on nonorthogonal atom-centered basis functions, into a Fock matrix based on orthogonal linear combinations of the original basis functions. With these new basisfunctions, i.e so that diagonalization of gives the eigenvectors (of the new basis functions, which are transformed back to those corresponding to the original set: and eigenvalues of H.

Because the overlap integrals needed by the EHM depend on molecular geometry, the method can in principle be used for geometry optimization, although for the conventional EHM the results are generally poor, so known geometries are used as input.

Introduction to Quantum Mechanics 153

Applications of the EHM involve largely the study of big molecules and polymeric systems, often containing heavy metals.

The strengths of the EHM derive from its simplicity: it is very fast and so can be applied to large systems; the only empirical parameters needed are (valence-state) ionization energies, which are available for a wide range of elements; the results of calculations lend themselves to intuitive interpretation since they depend only on geometry and ionization energies, and on occasion the proper treatment of overlap integrals even gives better results than those from more elaborate SE methods. The fact that the EHM is conceptually simple yet incorporates several features of more sophisticated methods enables it to serve as an excellent introduction to quantum mechanical computational methods.

The weaknesses of the EHM are due largely to its neglect of electron spin and electron–electron repulsion and the fact that it bases the energy of a molecule simply on the sum of the one-electron energies of the occupied orbitals, which ignores electron– electron repulsion and internuclear repulsion; this is at least partly the reason it usually gives poor geometries.

REFERENCES

[1] For general accounts of the development of quantum theory see: J. Mehra and H. Rechenberg, “The Historical Development of Quantum Theory”, Springer-Verlag, New York, 1982; T. S. Kuhn, “Black-body Theory and the Quantum Discontinuity 1894–1912”, Oxford University Press, Oxford, 1978. (b) An excellent historical and scientific exposition, at a somewhat advanced level: M. S. Longair, “Theoretical Concepts in Physics”, Cambridge University Press, Cambridge, 1983, chapters 8–12.

[2] A great deal has been written speculating on the meaning of quantum theory, some of it serious science, some philosophy, some mysticism. Some leading references are:

(a) A. Whitaker, “Einstein, Bohr and the Quantum Dilemma”, Cambridge University Press, 1996; (b) V. J. Stenger, “The Unconscious Quantum”, Prometheus, Amherst, NY, 1995; (c) P. Yam, Scientific American, June 1997, p. 124; (d) D. Z. Albert, Scientific American, May 1994, p. 58; (e) D. Z. Albert, “Quantum Mechanics and Experience”, Harvard University Press, Cambridge, MA, 1992; (f) D. Bohm and H. B. Hiley, “The Undivided Universe”, Routledge, New York, 1992; (g) J. Baggott, “The Meaning of Quantum Theory”, Oxford University Press, New York, 1992; (h) M. Jammer, “The Philosophy of Quantum Mechanics”, Wiley, New York, 1974.

[3]I. N. Levine, “Quantum Chemistry”, 5th Ed., Prentice Hall, Upper Saddle River, NJ, 2000.

[4]Sitzung der Deutschen Physikalischen Gesellschaft, 14 December 1900, Verhandlung 2, p. 237. This presentation and one of October leading up to it (Verhandlung 2, p. 202) were combined in: M. Planck, Annalen. Phys., 1901, 4(4), 553.

[5]M. J. Klein, Physics Today, 1966, 19, 23.

[6]For a good and amusing account of quantum strangeness (and relativity effects) and how things might be if Planck’s constant had a considerably different value, see G. Gamov and R. Stannard, “The New World of Mr Tompkins”, Cambridge University Press, Cambridge, 1999. This is based on the classics by George Gamow, “Mr Tompkins in Wonderland” (1940) and “Mr Tompkins Explores the Atom” (1944), which were united in “Mr Tompkins in Paperback,” Cambridge University Press, Cambridge, 1965.

154Computational Chemistry

[7]A. Einstein, Ann. Phys., 1905, 17, 132. Actually, the measurements are very difficult to do accurately, and the Einstein linear relationship may have been more a prediction than an explanation of established facts.

[8](a) For an elementary treatment of Maxwell’s equations and the loss of energy by an accelerated electric charge, see R. K. Adair, “Concepts in Physics,” Academic Press, New York, 1969, chapter 21. (b) For a brief historical introduction to Maxwell’s equations see M. S. Longair, “Theoretical Concepts in Physics”, Cambridge University Press, Cambridge, 1983, chapter 3. For a rigorous treatment of the loss of energy by an accelerated electric charge see Longair, chapter 9.

[9]N. Bohr, Phil. Mag., 1913, 26, 1.

[10]For example, S. T. Thornton and A. Rex, “Modern Physics for Scientists and Engineers”, Saunders, Orlando, FL., 1993, pp. 155–164.

[11]See, e.g. Ref. [2a], loc. cit.

[12]E. Schrödinger, Ann. Phys., 1926, 79, 361. This first Schrödinger equation paper, a nonrelativistic treatment of the hydrogen atom, has been described as “one of the greatest achievements of twentieth-century physics” (Ref. [13, p. 205]).

[13]W. Moore, “Schrödinger. Life and thought,” Cambridge University Press, Cambridge, 1989.

[14]L. de Broglie, “Recherche sur la Theorie des Quanta”, thesis presented to the faculty of sciences of the University of Paris, 1924.

[15]Ref. [13, chapter 6].

[16]For example, Ref. [3, pp. 410–419, 604–613].

[17]V. I. Minkin, M. N. Glukhovtsev, and B. Ya. Simkin, “Aromaticity and Antiaromaticity: Electronic and Structural Aspects,” Wiley, New York, 1994.

[18](a) Generalized VB method: R. A. Friesner, R. B. Murphy, M. D. Beachy, M. N. Ringnalda, W. T. Pollard, B. D. Dunietz, Y. Cao, J. Phys. Chem. A, 1999, 103, 1913, and references therein; (b) J. G. Hamilton and W. E. Palke, J. Am. Chem. Soc., 1993, 115, 4159.

[19]The pioneering benzene paper: E. Hückel, Z. Physik, 1931, 70, 204. Other papers by Hückel, on the double bond and on unsaturated molecules, are listed in his autobiography, “Ein Gelehrtenleben. Ernst und Satire,” Verlag Chemie, Weinheim, 1975, pp. 178–179.

[20]L. Pauling, “The Nature of the Chemical Bond,” 3 Ed., Cornell University Press, Ithaca, NY, 1960, pp. 111–126.

[21](a) A compact but quite thorough treatment of the SHM see Ref. [3], pp. 629–649.

(b) A good, brief introduction to the SHM is: J. D. Roberts, “Notes on Molecular Orbital Calculations”, Benjamin, New York, 1962. (c) A detailed treatment: A. Streitweiser, “Molecular Orbital Theory for Organic Chemists,” Wiley, New York, 1961. (d) The SHM and its atomic orbital and molecular orbital background are treated in considerable depth in “H. E. Zimmerman, “Quantum Mechanics for Organic Chemists,” Academic Press, New York, 1975. (e) Perhaps the definitive presentation of the SHM is E. Heilbronner and H. Bock, “Das HMO Modell und seine Anwendung,” Verlag Chemie, Weinheim, Germany, vol. 1 (basics and implementation), 1968; vol. 2, (examples and solutions), 1970; vol. 3 (tables of experimental and calculated quantities), 1970. An English translation of vol. 1 is available: “The HMO Model and its Application. Basics and Manipulation”, Verlag Chemie, 1976.

[22]For example Ref. [21b, pp. 87–90; [21c, pp. 380–391] and references therein; Ref. [21d, chapter 4].

Introduction to Quantum Mechanics 155

[23]See any introductory book on linear algebra.

[24]Ref. [21 c, chapter 1].

[25]J. Simons and J. Nichols, “Quantum Mechanics in Chemistry,” Oxford University Press, New York, 1997, p. 133.

[26]See, e.g. F. A. Carey and R. J. Sundberg, “Advanced Organic Chemistry. Part A,” 3rd Ed., Plenum, New York, 1990, pp. 30–34.

[27]Y. Jean and F. Volatron, “An Introduction to Molecular Orbitals,” Oxford University Press, New York, 1993, pp. 143–144.

[28] (a) P. A. Schultz and R. P. Messmer, J. Am. Chem. Soc., 1993, 115, 10925.

(b) P. B. Karadakov, J. Gerratt, D. L. Cooper, and M. Raimondi, J. Am. Chem. Soc., 1993, 115, 6863.

[29](a) T. H. Lowry and K. S. Richardson, “Mechanism and Theory in Organic Chemistry”, Harper and Row, New York, 1981, pp. 26, 270. (b) A. Streiwieser, R. A. Caldwell and G. R. Ziegler, J. Am. Chem. Soc., 1969, 91, 5081, and references therein.

[30]M. J. S. Dewar, “The Molecular Orbital Theory of Organic Chemistry,” McGraw-Hill, New York, 1969, pp. 92–98.

[31] (a) For a short review of the state of MO theory in its early days see R. S. Mulliken, J. Chem Phys., 1935, 3, 375. (b) A personal account of the development of MO theory: R. S. Mulliken,“Life of a Scientist: An Autobiographical Account of the Development of Molecular Orbital Theory with an Introductory Memoir by Friedrich Hund,” Springer-Verlag, New York, 1989. (c) For an account of the “tension” between the MO approach of Mulliken and the VB approach of Pauling see A. Simões and K. Gavroglu in “Conceptual Perspectives in Quantum Chemistry,” J.-L. Calais and E. Kryachko, Eds., Kluwer Academic Publishers, London, 1997.

[32]L. Pauling, Chem. Rev., 1928, 5, 173.

[33]J. E. Lennard-Jones, Trans. Faraday Soc., 1929, 25, 668.

[34]C. A. Coulson and I. Fischer, Philos. Mag., 1949, 40, 386.

[35]Ref. [21d, pp. 52–53].

[36]As Dewar points out in Ref. [30], this derivation is not really satisfactory. A rigorous approach is a simplified version of the derivation of the Hartree–Fock equations (section 5.2.3). It starts with the total molecular wavefunction expressed as a determinant, writes the energy in terms of this wavefunction and the Hamiltonian and finds the condition for minimum energy subject to the molecular orbitals being orthonormal (cf. orthogonal matrices, section 4.3.3). The procedure is explained in some detail in section 5.2.3).

[37]See, e.g. D. W. Rogers, “Computational Chemistry Using the PC,” VCH, New York, 1990, pp. 92–94.

[38]R. B. Woodward and R. Hoffmann, “The Conservation of Orbital Symmetry,” Verlag Chemie, Weinheim, Germany, 1970.

[39](a) For a nice review of the cyclobutadiene problem see B. K. Carpenter in “Advances in Molecular Modelling,” JAI Press, Greenwich, Connecticut, 1988. (b) Calculations on the degenerate interconversion of the rectangular geometries: J. C. Santo-García, A. J. PérezJim6néz, and F. Moscardó Chem. Phys. Letter, 2000, 317, 245.

156Computational Chemistry

[40](a) Strictly speaking, cyclobutadiene exhibits a pseudo-Jahn–Teller effect: D. W. Kohn and P. Chen, J. Am. Chem. Soc., 1993, 115, 2844. (b) For “A beautiful example of the Jahn– Teller effect” see M. Hargittai, J. Am. Chem. Soc., 1997, 119, 9042. (c) Review:

T.A. Miller, Angew. Chem. Int. Ed., 1994, 33, 962.

[41]A. A. Frost and B. Musulin, J. Chem. Phys., 1953, 21, 572.

[42]W. E. Doering and L. H. Knox, J. Am. Chem. Soc., 1954, 76, 3203.

[43]M. J. S. Dewar, “The Molecular Orbital Theory of Organic Chemistry,” McGraw-Hill, New York, 1969, pp. 95–98.

[44]M. J. S. Dewar, “The Molecular Orbital Theory of Organic Chemistry,” McGraw-Hill, New York, 1969, pp. 236–241.

[45](a) Ref. [17, pp. 157–161]. (b) K. Krogh-Jespersen, P. von R. Schleyer, J. A. Pople, and D. Cremer, J. Am. Chem. Soc., 1978, 100, 4301. (c) The cyclobutadiene dianion, another potentially aromatic system, has recently been prepared: K. Ishii, N. Kobayashi, T. Matsuo, M. Tanaka, A. Sekiguchi, J. Am. Chem. Soc., 2001,123, 5356.

[46]S. Zilberg and Y. Haas, J. Phys. Chem. A, 1998, 102, 10843, 10851.

[47]The most rigorous approach to assigning electron density to atoms and bonds within molecules is the atoms-in molecules (AIM) method of Bader and coworkers: R. F. W. Bader, “Atoms in Molecules,” Clarendon Press, Oxford, 1990.

[48]Various approaches to defining bond order and atom charges are discussed in F. Jensen, “Introduction to Computational Chemistry,” Wiley, New York, 1999, chapter 9.

[49]Ref. [17, pp. 177–180].

[50]For leading references see: (a) B. A. Hess and L. J. Schaad, J. Chem. Educ., 1974, 51, 640; (b) B. A. Hess and L. J. Schaad, Pure and Appl. Chem., 1980, 52, 1471.

[51]See, e.g. Ref. [21c, chapters 4 and 5].

[52]See, e.g. Ref. [21c, pp. 13, 16].

[53](a) R. Hoffmann, J. Chem. phys., 1963, 39, 1397; (b) Hoffmann, J. Chem. Phys, 1964, 40, 2474; (c) R. Hoffmann, J. Chem. Phys., 1964, 40, 2480; (d) R. Hoffmann, J. Chem. Phys., 1964, 40, 2745; (e) R. Hoffmann, Tetrahedron, 1966, 22, 521; (f) R. Hoffmann, Tetrahedron, 1966, 22, 539; (g) P. J. Hay, J. C. Thibeault, R. Hoffmann J. Am. Chem. Soc., 1975, 97, 4884.

[54]M. Wolfsberg and L. Helmholz, J. Chem. Phys., 1952, 20, 837.

[55] Actually, valence state ionization energies are usually used; see H. O. Pritchard,

H.A. Skinner, Chem. Rev., 1955, 55, 745; J. Hinze, H. H. Jaffe, J. Am. Chem. Soc., 1962, 84, 540; A. Stockis, R. Hoffmann J. Am. Chem. Soc., 1980, 102, 2952.

[56]F. L. Pilar, “Elementary Quantum Chemistry,” McGraw-Hill, New York, 1990, pp. 493– 494.

[57]A. Szabo and N. S. Ostlund, “Modern Quantum Chemistry,” McGraw-Hill, 1989, pp. 168-

179.This describes an ab initio (chapter 5) calculation on but gives information relevant to our EHM calculation.

[58]C. C. J. Roothaan, J. Chem. Phys., 1951, 19, 1445.

[59]R. Hoffmann, “Solids and Surfaces: A Chemist’s View of Bonding in Extended Structures.” VCH publishers, 1988.

[60](a) A polymeric rhenium compound: H. S. Genin, K. A. Lawlwr, R. Hoffmann,

W.A. Hermann, R. W. Fischer, and W. Scherer, J. Am. Chem. Soc., 1995, 117, 3244.