Introduction to Quantum Mechanics 95

there is a mathematical function obtained by combining the appropriate 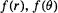and

The function 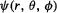(clearly could also be expressed in Cartesians), depends functionally on and parametrically on n, l and for each particular set of these numbers there is a particular function with the spatial coordinates variables A function like k sin x is a function of x and depends only parametrically on k. This function is an orbital (“quasi-orbit”; the term was invented by Mulliken, section 4.3.4), and you are doubtless familiar with plots of its variation with the spatial coordinates. Plots of the variation of with spatial coordinates indicate variation of the electron density (recall the Born interpretation of the wavefunction) in space due to an electron with quantum numbers and We can think of an orbital as a region of space occupied by an electron with a particular set of quantum numbers, or as a mathematical function describing the energy and the shape of the spatial domain of an electron. For an atom or molecule with more than one electron, the assignment of electrons to orbitals is an (albeit very useful) approximation, since orbitals follow from solution of the Schrödinger equation for a hydrogen atom.

The Schrödinger equation that we have been talking about is actually the timeindependent (and nonrelativistic) Schrödinger equation: the variables in the equation are spatial coordinates, or spatial and spin coordinates (section 5.2.3.1) when electron spin is taken into account. The time-independent equation is the one most widely-used in computational chemistry, but the more general time-dependentSchrödingerequation, which we shall not examine, is important in certain applications, like some treatments of the interaction of a molecule with light, since light (radiation) is composed of timevarying electric and magnetic fields. The time-dependent density functional theory (DFT) method of calculating UV spectra (chapter 7) is based on the time-dependent Schrödinger equation.

4.3THE APPLICATION OF THE SCHRÖDINGER EQUATION TO CHEMISTRY BY HÜCKEL

4.3.1Introduction

The quantum mechanical methods described in this book are all molecular orbital (MO) methods, or oriented toward the MO approach: ab initio and SE methods use the MO method, and density functional methods are oriented toward the MO approach. There is another approach to applying the Schrödinger equation to chemistry, namely the valence bond (VB) method. Basically the MO method allows atomic orbitals (AOs) to interact to create the MO of a molecule, and does not focus on individual bonds as shown in conventional structural formulas. The VB method, on the other hand, takes the molecule, mathematically, as a sum (linear combination) of structures each of which corresponds to a structural formula with a certain pairing of electrons [16], The MO method explains in a relatively simple way phenomena that can be understood only with difficulty using the VB method, like the triplet nature of dioxygen or the fact that

96 Computational Chemistry

benzene is aromatic but cyclobutadiene is not [17]. With the application of computers to quantum chemistry the MO method almost eclipsed the VB approach, but the latter has in recent years made a limited comeback [18].

The first application of quantitative quantum theory to chemical species significantly more complex than the hydrogen atom was the work of Hückel20 on unsaturated organic compounds, in 1930–1937 [19]. This approach, in its simplest form, focuses on the p electrons of double bonds, aromatic rings and heteroatoms. Although Hückel did not initially explicitly consider orbital hybridization (the concept is usually credited to Pauling,21 1931 [20]), the method as it became widely applied [21] confines itself to planar arrays of -hybridized atoms, usually carbon atoms, and evaluates the consequences of the interactions among the p electrons (Fig. 4.4). Actually, the simple Hückel method has been occasionally applied to nonplanar systems [22]. Because of the importance of the concept of hybridization in the simple Hückel method a brief discussion of this concept is warranted.

4.3.2Hybridization

Hybridization is the mixing of orbitals on an atom to produce new, “hybridized” (in the spirit of the biological use of the term), AOs. This is done mathematically but can be appreciated pictorially (Fig. 4.5). One way to justify the procedure theoretically is to

20Erich Hückel, born Berlin, 1896. Ph.D. Göttingen. Professor, Marburg. Died Marburg, 1980.

21Linus Pauling, born Portland, Oregon, 1901. Ph.D. Caltech. Professor, Caltech. Known for work in quantum chemistry and biochemistry, campaign for nuclear disarmament, and controversial views on vitamin C. Nobel prize for chemistry 1954, for peace 1963. Died near Big Sur, CA, 1994.

Introduction to Quantum Mechanics 97

recognize that AOs are vectors in the generalized mathematical sense of being elements of a vector space [23] (if not in the restricted sense of the physicist as physical entities with magnitude and direction); it is therefore permissible to take linear combinations of these vectors to produce new members of the vector space. A good, brief introduction to hybridization in is given by Streitwieser [24].

In a familiar example, a 2s orbital can be mixed with three 2p orbitals to give four hybrid orbitals; this can be done in an infinite number of ways, such as (from now on

will be used for AOs and for MOs):

or

Both the set (4.33) and the set (4.34) consist of four orbitals, since the electron density contributions from the component s and p orbitals to the hybrid is, in each case (considering the squares of the coefficients; recall the Born interpretation of the square of a wavefunction, section 4.2.6) in the ratio 1 : 3, i.e. and and in each set we have used a total of one s orbital, and one each of the and orbitals. The total electron density from each component orbital is unity, e.g. for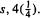

Hybridization is purely a mathematical procedure, originally invented to reconcile the quantum mechanical picture of electron density in s, p, etc. orbitals with traditional views of directed valence. For example, it is sometimes said that in the absence of hybridization combining a carbon atom with four unpaired electrons with four hydrogen atoms would give a methane molecule with three equivalent, mutually perpendicular bonds and a fourth, different, bond (Fig. 4.6). Actually, this is incorrect: the 2s and three 2p orbitals of an unhybridized carbon along with the four 1s orbitals of four hydrogen atoms provide, without invoking hybridization, a tetrahedrally symmetrical

98 Computational Chemistry

valence electron distribution that leads to tetrahedral methane with four equivalent bonds (Fig. 4.6). In fact, it has been said “It is sometimes convenient to combine AOs to form hybrid orbitals that have well defined directional character and then to form MOs by combining these hybrid orbitals. This recombination of AOs to form hybrids is never necessary…” [25]. Interestingly, the MOs accommodating the four highest-energy electron pairs of methane (the eight valence electrons) are not equivalent in energy (not degenerate). This is an experimental fact that can be shown by photoelectron spectroscopy [26]. Instead of four orbitals of the same energy we have three degenerate orbitals and one lower in energy (and of course the almost undisturbed 1s core orbital of carbon). This surprising arrangement is a consequence of the fact that symmetry requires one combination (i.e. one MO) of carbon and hydrogen orbitals (essentially a weighted sum of the C2s and the four His orbitals) to be unique and the other three AO combinations (the other three MOs) to be degenerate (they involve the C2p and the H1s orbitals) [26,27]. It must be emphasized that although the methane valence orbitals are energetically different, the electron and nuclear distribution is tetrahedrally symmetrical – the molecule indeed has (section 2.6) symmetry. The four MOs formed directly from AOs are the canonical MOs. They are delocalized (spread out over the molecule), and do not correspond to the familiar four bonding H1s MOs, each of which is localized between the carbon nucleus and a hydrogen nucleus. However, the canonical MOs can be mathematically manipulated to give the familiar localized MOs (section 5.2.3.1).

Introduction to Quantum Mechanics 99

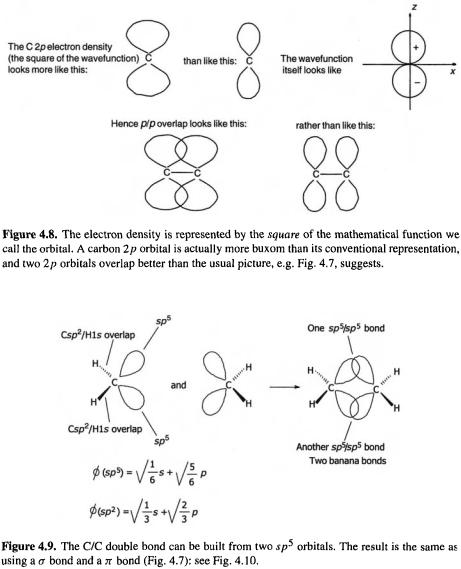
Another example illustrates a situation somewhat similar to that we saw with methane, and what was until fairly recently a serious controversy: the best way to represent the carbon/carbon double bond [28]. The currently popular way to conceptualize the bond has it resulting from the union of two hybridized carbon atoms (Fig. 4.7); the orbitals on each carbon overlap end-on forming a bond and the p orbitals on each carbon overlap sideways forming a bond. Note that the usual depiction of a carbon p orbital is unrealistically spindle-shaped, necessitating depicting overlap with connecting lines as in Fig. 4.7. Figure 4.8 shows a picture in better accord with the calculated electron density in the p orbital, i.e. corresponding to the square of the wavefunction. The two leftover orbitals can be used to bond to, say, hydrogen atoms, as shown. From this viewpoint the double bond is thus composed of a bond and a bond. However, this is not the only way to represent the bond. One can, for example, mathematically construct a carbon atom with two orbitals and two 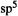orbitals; the union of two such carbons gives a double bond formed from two bonds (Fig. 4.9), rather than from a bond and a bond. Which is right? They are only different ways of viewing the same thing: the electron density in the bond decreases smoothly from the central C/C axis in both models (Fig. 4.10), and the experimental NMR coupling constant for the C–H bond would, in both models, be predicted to correspond to about 33% s character in the orbital used by carbon to bond to hydrogen [29]. The ability of the hybridization concept to correlate and rationalize acidities of hydrocarbons in terms of the s character of the carbon orbital in a C–H bond [29] is an example of the usefulness of this idea. Most of the systems studied by the simple Hückel method are essentially flat, as expected for arrays, and many