EASIER QUESTIONS

Semiempirical Calculations 383

2.Molecular mechanics is essentially empirical, while methods like PPP, CNDO, and AM1/PM3 are semiempirical. What are the analogies in PPP etc. to MM procedures of developing and parameterizing a forcefield? Why are PPP etc. only semiempirical?

3.What do you think are the advantages and disadvantages of parameterizing SE methods with data from ab initio calculations rather than from experiment? Could a SE method parameterized using ab initio calculations logically be called semiempirical?

4.There is a kind of contradiction in the Dewar-type methods (AM1, etc.) in that overlap integrals are calculated and used to help evaluate the Fock matrix elements, yet the overlap matrix is taken as a unit matrix as far as diagonalization of the Fock matrix goes. Discuss.

5.What would be the advantages and disadvantages of using the general MNDO/AM1 parameterization procedure, but employing a minimal basis set instead of a minimal valence basis set?

6.In SCF SE methods major approximations lie in the calculation of the and integrals of the Fock matrix elements (Eq. (6.1)). Suggest an alternative approach to approximating one of these integrals.

7.Read the exchange between Dewar on the one hand and Halgren, Kleir and Lipscomb on the other [27], Do you agree that SE methods, even when they give good results “inevitably obscure the physical bases for success (however striking) and failure alike, thereby limiting the prospects for learning why the results are as they are?” Explain your answer.

8.It has been said of SE methods: “They will never outlive their usefulness for correlating properties across a series of molecules... I really doubt their predictive value for a one-off calculation on a small molecule on the grounds that whatever one is seeking to predict has probably already been included in with the parameters.” (A. Hinchliffe, “Ab Initio Determination of Molecular Properties,” Adam Hilger,

Bristol, 1987, p. x). Do you agree with this? Why or why not? Compare the above quotation with Ref. [23, pp. 133–136].

9.For common organic molecules Merck Molecular Force field geometries are nearly as good as geometries (section 3.4). For such mole-

10. Semiempirical methods are untrustworthy for “exotic” molecules of theoretical interest. Give an example of such a molecule and explain why it can be considered exotic. Why cannot SE methods be trusted for molecules like yours? For what other kinds of molecules might these methods fail to give good results?

This page intentionally left blank

Chapter 7

Density Functional Calculations

My other hope is that ... a basically new ab initio treatment capable of giving

chemically accurate results a priori, is achieved soon.

M. J. S. Dewar, A Semiempirical Life, 1992.

7.1 PERSPECTIVE

We have seen three broad techniques for calculating the geometries and energies of molecules: molecular mechanics (chapter 3), ab initio methods (chapter 5), and semiempirical methods (chapters 4 and 6). Molecular mechanics is based on a balls- and-springs model of molecules. Ab initio methods are based on the subtler model of the quantum mechanical molecule, which we treat mathematically starting with the Schrödinger equation. Semiempirical methods, from simpler ones like the Hückel and extended Hückel theories (chapter 4) to the more complex SCF semiempirical theories (chapter 6), are also based on the Schrödinger equation, and in fact their “empirical” aspect comes from the desire to avoid the mathematical problems that this equation imposes on ab initio methods. Both the ab initio and the semiempirical approaches calculate a molecular wavefunction (and molecular orbital energies), and thus represent wavefunction methods. However, a wavefunction is not a measurable feature of a molecule or atom – it is not what physicists call an “observable;” in fact there is no general agreement among physicists what, if anything, a wavefunction is[1].

Density functional theory (DFT) is based not on the wavefunction, but rather on the electron probability density function or electron density function, commonly called simply the electron density or charge density, designated by This is a probability per unit volume; the probability offindingan electron in a volume element dxdy dz centered on a point with coordinates x, y, z is 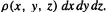The units of are logically and since the units of dx dy dz are volume, is a pure number, a probability. However, if we regard the charge on the electron as our unit of charge then has units of electronic charge and

units of electronic charge. If we think of electronic charge as being smeared out in a fog

on a point P(x,y,z) corresponds to the amount of fog in the volume element dx dy dz. In a scatterplot of electron density in a molecule, the variation of 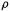with position can be indicated by the density of the points. The electron density function is the basis not only of DFT, but of a whole suite of methods of regarding and studying atoms and molecules [2], and, unlike the wavefunction, is measurable, e.g. by X-ray diffraction or electron diffraction [3]. Apart from being an experimental observable and being readily grasped intuitively [4], the electron density has another property particularly suitable for any method with claims to being an improvement on, or at least a valuable alternative to, wavefunction methods: it is a function of position only, that is, of just three variables (x, y, z), while the wavefunction of an n-electron molecule is a function of 4n variables, three spatial coordinates and one spin coordinate, for each electron. No matter how big the molecule may be, the electron density remains a function of three variables, while the complexity of the wavefunction increases with the number of electrons. The term functional, which is akin to function, is explained in section 7.2.3.1. To the chemist, the main advantage of DFT is that in about the same time needed for an HF calculation one can often obtain results of about the same quality as from MP2 calculations (section 7.3). Chemical applications of DFT are but one aspect of an ambitious project to recast conventional quantum mechanics, i.e. wave mechanics, in a form in which “the electron density, and only the electron density, plays the key role” [5]. It is noteworthy that the 1998 Nobel Prize for chemistry was awarded to John Pople (section 5.3.3), largely for his role in developing practical wavefunctionbased methods, and Walter Kohn1, for the development of density functional methods [6].

A question sometimes asked is whether DFT should be regarded as a special kind of ab initio method. The case against this view is that the correct mathematical form of the DFT functional is not known, in contrast to conventional ab initio theory where the correct mathematical form of the fundamental equation, the Schrödinger equation, is (we think), known. In conventional ab initio theory, the wavefunction can be improved systematically by going to bigger basis sets and higher correlation levels, which takes us closer and closer to an exact solution of the Schrödinger equation, but in DFT there is so far no known way to systematically improve the functional (section 7.2.3.2); one must feel one’s way forward with the aid of intuition and comparison of the results with experiment and of high-level conventional ab initio calculations. In this sense current DFT is semiempirical, but the limited use of empirical parameters (typically from zero to about 10), and the possibility of one day finding the exact functional makes it ab initio in spirit. Were the exact functional known, DFT might indeed give “chemically accurate results a priori.”

1Walter Kohn, born in Vienna in 1923. B.A., B.Sc., University of Toronto, 1945, 1946. Ph.D. Harvard, 1948. Instructor in physics, Harvard, 1948–1950. Assistant, Associate, full Professor, Carnegie Mellon University, 1950–1960. Professor of physics, University of California at Santa Diego, 1960–1979; University of California at Santa Barbara 1979–present. Nobel Prize in chemistry 1998.