Ab initio calculations 307

the diagonal elements are the number of electrons in the “atomic space” of the basis functions, and the off-diagonal elements are the number of electrons in the overlap space of the basis functions.

The Mulliken approach to population analysis has certain problems; for example, it sometimes assigns more than two electrons, and sometimes a negative number of electrons, to an orbital. It is also fairly basis-set dependent (Hehre, Radom, Schleyer and Pople compare Mulliken charges for a variety of molecules using the STO-3G, 3-21G(*) and 6-31G* basis sets: [1g], pp. 337–339). Other approaches to partitioning electrons among orbitals and thus calculating charges and bond orders are the Löwdin method [167] and the natural atomic orbitals (NAO) population analysis of Weinhold [168].

Electrostatic potential

The electrostatic potential (ESP) is a measure of charge distribution that also provides other useful information [169]. The electrostatic potential at a point P in a molecule is defined as the amount of energy (work) needed to bring a unit point positive “probe charge” (e.g. a proton) from infinity to P. The electrostatic potential can be thought of as a measure of how positive or negative the molecule is at P: a positive value at the point means that the net effect experienced by the probe charge as it was brought from infinity was repulsion, while a negative value means that the probe charge was attracted to P, i.e. energy was released as it fell from infinity to P. The ESP at a point is the net result of the effect of the positive nuclei and the negative electrons. The calculation of the effect of the nuclei is trivial, following directly from the fact that the potential due to a point charge Z at a distance r away from the unit charge is

Thus the ESP created by the nuclei is

where is the distance from nucleus A to the point P, i.e. the absolute value of the difference of two vectors.To obtain the expression for the ESP due to the electrons, we can modify Eq. (5.227) by replacing the summation over the nuclei by an integral over infinitesimal volume elements of the electron density or chargedensity (see

Atoms-in-molecules). The total ESP is:

The ESP at many points on the surface of the molecule can be calculated (section 5.5.6) and a set of atom charges then calculated to fit (by a least-squares procedure) the ESP values, and also to sum to the net charge on the molecule (the use of visualization of the ESP is discussed in section 5.5.6).

308 Computational Chemistry

Values of Mulliken and Löwdin bond orders, and Mulliken, natural and ESP atom charges, are compared in Table 5.19, for hydrogen fluoride. We see that the Mulliken charges vary considerably, but apart from the STO-3G values, the electrostatic charges vary very little, and the natural charges little, with the level of calculation. Bond orders, however, are quite sensitive to the level of calculation. The utility of charges and bond orders lies not in their absolute values, but rather in the fact that a comparison of, say, Löwdin charges or bond orders, calculated at the same level for a series of molecules, can provide insights into a trend. For example, one might argue that the electronwithdrawing power of a series of groups A, B, etc. could be compared by comparing the C/C bond orders in etc. Bond orders have been used to judge whether a species is free or really covalently bonded, and have been proposed as an index of progress along a reaction coordinate [170].

Atoms-in-molecules

A method of calculating charges and bond orders that may be less arbitrary than any of those mentioned so far is based on the theory of atoms in molecules (AIM), developed by Bader and coworkers [171]. The AIM approach rests on analyzing the variation from place to place in a molecule of the electron density function (electron probability function, charge density function, charge density), This is a function which gives the variation of the total electron density from point to point in the molecule;

is the probability of finding an electron in an infinitesimal volume centered on the point with coordinates (x, y, z) (the probability of finding more than one electron in is infinitesimal). The electron probability density can be calculated from the wavefunction. It is not, as one might have thought, simply where is the multielectron wavefunction of space and spin coordinates (section 5.2.3.1). This latter is the function for the variation from point to point of the probability of finding electron 1 with a specified spin, electron 2 with a specified spin, etc., at points (x, y, z). If we think of the electrons being smeared out in a fog around

Ab initio calculations 309

the molecule, then the variation of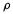 from point to point corresponds to the varying density of the fog, and centered on a point P corresponds to the amount of fog in the volume element dxdydz. Alternatively, in a scatterplot of electron density in a molecule, the variation of with position can be indicated by varying the volume density of the points. For more on the electron density function see sections 7.1 and 7.2.1.

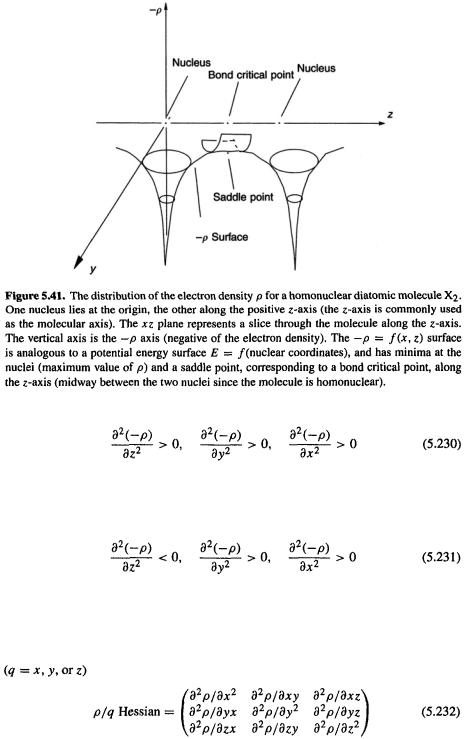
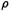Consider first the electron density around an atom. As we approach the nucleus this rises toward a maximum, or the negative of the electron density, falls toward a minimum (Fig. 5.40). Viewing the electron distribution in terms of rather than is useful because it more easily enables us to discern analogies between the variation of in a molecule (in a vs. location-in-molecule graph), and a potential energy surface, which is the variation of energy with geometry (an E vs. geometry graph). Examine the distribution of in a homonuclear diatomic molecule 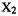(Fig. 5.41). This shows a plot of vs. two of the three Cartesian coordinates needed to assign positions to all the points in the molecule. The graph retains the internuclear axis (by convention the 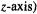and one other axis, say y; the molecule is symmetrical with respect to reflection in the yz plane. The negative of the electron density, dips toward a minimum at

the atomic nuclei goes toward a maximum). The nuclei correspond to stationary points, where the surface has zero slope (if we ignore the fact that, strictly speaking, the nonrelativistic density forms a cusp at a nucleus, i.e. the derivative of

becomes discontinuous) and from whence it goes upward in all directions. Thus the first derivative of with respect to all spatial coordinates is zero, and the second derivative is positive:

310 Computational Chemistry

and

Moving along the internuclear line we find a point in a saddle-shaped region, analogous to a transition state, where the surface again has zero slope (all first derivatives zero), and is negatively curved along the but positively curved in all other directions (Fig. 5.41), i.e.

This transition-state-like point is called a bond critical point. All points at which the first derivatives are zero are critical points, so the nuclei are also critical points. Analogously to the energy/geometry Hessian of a potential energy surface, an electron density function critical point (stationary point; relative maximum or minimum or saddle point) can be characterized in terms of its second derivatives by diagonalizing the Hessian

to get the number of positive and negative eigenvalues:

Ab initio calculations 311

For the surface of Fig. 5.41 the number of positive and negative eigenvalues for a nuclear critical point are 3 and 0, and for a bond critical point, 2 and 1. Thus for the surface to which the Hessian of Eq. (5.232) refers (the mirror image of the surface), the number of positive and negative eigenvalues is, respectively, 0 and 3 (for a nucleus), and 1 and 2 (for a bond critical point).

The minimum path (maximum- path) from one X nucleus to the other is the bond path; with certain qualifications this can be regarded as a bond. It is analogous to the minimum-energy path connecting a reactant and its products, i.e. to the intrinsic reaction coordinate. Such a bond is not necessarily a straight line: in strained molecules it may be curved. The bond passes through the bond critical point, (which for a homonuclear diatomic molecule is the midpoint between of the internuclear line). Now consider Fig. 5.42, which shows the molecule viewed along the The contour lines represent electron density, which rises as we approach a nucleus and falls off as we go to and beyond the van der Waals surface. If it is true that the molecule can be divided into atoms, then for the dividing surface S (represented as a vertical line in Fig. 5.42) must lie midway between the nuclei, with the internuclear line being normal to S and meeting S at the bond critical point. The electron density defines a gradient vector field, the totality of the trajectories each of which results from starting at infinity and moving along the path of steepest increase in Figure 5.42 shows that only two of the trajectories (of those in the plane of the paper) that originate at infinity do not end at the nuclei; these end at the bond critical point. These two trajectories define the intersection of S with the plane of the paper. None of the trajectories cross S, which is