5.3.3Types of basis sets and their uses

Ab initio calculations 217

to optimize Slater functions for atoms or small molecules, i.e. to find the values of that give the lowest energy for these, and then to use a least-squares procedure to fit contracted Gaussians to the optimized Slater functions [35].

STO-3G

This is a called a minimal basis set, although some atoms actually have more basis functions (which for this basis can be equated with atomic orbitals) than are needed to accommodate all their electrons. For the earlier part of the periodic table (hydrogen to argon) each atom has one basis function corresponding to its usual atomic orbital description, with the proviso that the orbitals used by the later atoms of a row are available to all those of the row. A hydrogen or helium atom has a 1s basis function. Each “first-row” atom (lithium to neon) has a 1s, a 2s, and a and function, giving 5 basis functions for each of these atoms: although lithium and beryllium are often not thought of as using p orbitals, all the atoms of this row are given the same basis, because this has been found to work better than a literally minimum basis set. Second-row atoms (sodium to argon) have a 1s and a 2s, as well as three 2p functions, plus a 3s and three p functions, giving 9 basis functions. In the third row, potassium and calcium, as expected, have the 9 functions of the previous row, plus a 4s and three 4p functions, for a total of 13 basis functions. Starting with the next element, scandium, five 3d orbitals are added, so that scandium to krypton have 13 + 5 = 18 basis functions. The STO-3G basis is summarized in Fig. 5.13(a).

The STO-3G basis introduces us to the concept of contraction shells in constructing contracted Gaussians from primitive Gaussians (section 5.3.2). The Gaussians of a contraction shell share common exponents. Carbon, e.g. has one s shell and one sp shell. This means that the 2s and 2p Gaussians (belonging to the 2sp shell) share common exponents (which differ from those of the 1s function). Consider the contracted

Gaussians

The usual practice is to set and 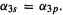Using common for the s and p primitives reduces the number of distinct integrals that must be calculated. An STO-3G calculation on for example, involves 9 basis functions (5 for C and 1 for each H) in 6 shells: for C one s (i.e. a 1s) shell, and one sp (i.e. a 2s plus 2p) shell, and for each H one s (i.e. a 1s) shell. The current view is that the STO-3G basis is not very good, and it would normally be considered unacceptable for research. Nevertheless, one hesitates to endorse Dewar and Storch’s assertion that “it must be considered obsolete” [36]. We do not know how many publications report work which began with a preliminary and unreported but valuable investigation using this basis. Its advantages are speed (it is probably the smallest basis set that would even be considered for an ab initio calculation) and the ease with which the molecular orbitals can be dissected into atomic orbital contributions. The STO-3G basis is

218 Computational Chemistry

Ab initio calculations 219

220 Computational Chemistry

Ab initio calculations 221

roughly twice as fast as the next larger commonly used one, the (Table 5.3). Sophisticated semiempirical methods (chapter 6) are perhaps more likely to be used nowadays in preliminary investigations, and to obtain reasonable starting structures for ab initio optimizations, but for systems significantly different from those for which the semiempirical methods were parameterized one might prefer to use the STO-3G basis. As for examining atomic contributions to bonding, interpreting bonding in terms of hybrid orbitals and the contribution of particular atoms to MO’s is simpler when each atom has just one conventional orbital, rather than split orbitals (as in the basis sets to be discussed). Thus a fairly recent analysis of the electronic structure of threeand four-membered rings used the STO-3G basis explicitly for this reason [37], as did an interpretation of the bonding in the unusual molecule pyramidane [38].

The shortcomings (and virtues) of the STO-3G basis are extensively documented throughout in [1g]. Basically, the drawbacks are that by comparison with the

basis, which is not excessively more demanding of time, it gives significantly less accurate geometries and energies (this was the reason for the call to abandon this basis [36]). Actually, even for second-row atoms (Na–Ar), where the defects of such a small basis set should be, and are, most apparent, the STO-3G basis supplemented with five

222 Computational Chemistry

d or polarization functions (the STO-3G* basis; polarization functions are discussed below) can give results comparable to those of the basis set. Thus for the S–O bond length of 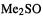we get (Å): STO-3G, 1.820; STO-3G*, 1.480; 3-21G, 1.678; 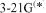, 1.490; exp., 1.485, and for NSF [39] the geometries shown in Fig. 5.14.

orbital into two parts, an inner shell and an outer shell. The basis function of the inner shell is represented by two Gaussians, and that ofthe outer shell by one Gaussian (hence the “21”); the core orbitals are each represented by one basis function, each composed of three Gaussians (hence the “3”). Thus H and He have a 1s orbital (the only valence

one Gaussian, making 9 basis functions. The terms inner and outer derive from the fact that the Gaussian of the outer shell has a smaller than the Gaussians of the inner shell, and so the former function falls off more slowly, i.e. it is more diffuse and effectively spreads out further, into the outer regions of the molecule. The purpose of splitting the valence shell is to give the SCF algorithm more flexibility in adjusting the contributions of the basis functions to the molecular orbitals, thus achieving a more

Ab initio calculations 223

Thirteen basis functions (“atomic orbitals”) give thirteen LCAO MOs:

Note that since there are thirteen MO’s but only eight electrons to be accommodated, only the first four MOs are occupied (recall that we are talking about closed-shell molecules in the ground electronic state). The nine empty MOs are called unoccupied or virtual molecular orbitals. We shall see that virtual MOs are important in certain kinds of calculations. Now, in the course of the SCF process the coefficients of the various innerand outer-shell basis functions can be varied independently to find the bestwavefunctions (those corresponding to the lowest energy). As the iterations proceed some outer-shell functions, say, could be given greater (or lesser) emphasis, independently of any inner-shell functions, allowing a finer-tuning of the electron distribution, and a lower energy, than would be possible with unsplit basis functions.

much less widely used than split valence sets, since the former are computationally more demanding and for many purposes only the contributions of the “chemically active” valence functions to the MOs need to be fine-tuned, and in fact “double zeta”

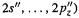functions, for a total of 9 basis functions. These inhabit three contraction shells (see the STO-3G discussion): a 1s, an sp inner and an sp outer contraction shell. Sodium to argon have a 1s, a 2s and three 2p functions, and an inner and outer shell of 3s and 3p functions, for a total of 1+ 4 + 8 = 13 basis functions. These are in four shells: a 1s, an sp (2s, 2p), an sp inner and an sp outer (3s and 3p inner, 3s and 3p outer). Potassium and calcium have a 1s, a 2s and three 2p, and a 3s and three 3p functions, plus inner and outer 4s and 4p functions, for a total of 1+4+4+8= 17 basis

224 Computational Chemistry

functions. For the remaining atoms for which the 3-21G basis is available d functions are added. The 3-21G basis set is summarized in Fig. 5.13(b).

For molecules with atoms beyond the first row (beyond neon), this “pure” 3-21G basis tends to give poor geometries. This problem is largely overcome for secondrow elements (sodium to argon) by supplementing this basis with d functions, called polarization functions. The term arises from the fact that d functions permit the electron distribution to be polarized (displaced along a particular direction), as shown in Fig. 5.16. Polarization functions enable the SCF process to establish a more anisotropic electron distribution (where this is appropriate) than would otherwise be possible (cf. the use of split valence basis sets to permit more flexibility in adjusting the inner and outer regions of electron density). The 3-21G basis set augmented where appropriate with d functions is called the basis; the asterisk indicates polarization functions (d in this case), and the parentheses mean that the extra (compared to the “pure” 3-21G basis) polarization functions are present only beyond the first row. For H to Ne, the 3-21G and the basis sets are identical, and for these first-row atoms the term 3-21G, rather than is normally used. The 3-21G basis without the supplementary d polarization functions is not normally employed for atoms beyond neon: here the usual 3-21G-type basis set is the There is also a relatively little-used basis, the 3-21G* (no parentheses) in which a set of six d functions is added to the firstrow elements, giving carbon, say, 15 rather than nine basis functions. The

basis (with parentheses) is summarized in Fig. 5.13(c). p-Polarization functions can also be added to hydrogens and helium (below).

Ab initio calculations 225

Examples of geometries calculated with the 3-21G and basis sets are shown in Fig. 5.14. The 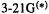gives remarkably good geometries for such a small basis set, and in fact it is used for the geometry optimization step of some high-accuracy energy methods (section 5.5.2). Since it is roughly ten times as fast (Table 5.3) as the next widely-used basis, the 6-31G* (below) and is much less demanding of computer power, the basis set is a kind of workhorse for relatively big molecules; see for example a study using it for geometry optimization investigations ofpericyclic reactions [40]. The somewhat similar but less popular 4-21G basis was used, with the 3-21G* basis on sulfur, for geometry optimization of the protein crambin, with 46 amino acid residues and 642 atoms. This represented 3597 basis functions, and the job took 260 days [41]. Even where geometry optimizations with larger bases are practical, a survey of the problem with the 3-21G* basis is sometimes useful (it is geometries rather than relative energies which are good; consistently getting good relative energies is a more challenging problem - see section 5.5.2).

6-31G*

This is a split valence basis set with polarization functions (these terms were explained in connection with the basis set, above). The valence shell of each atom is split into an inner part composed of three Gaussians and an outer part composed of one Gaussian (“31”), while the core orbitals are each represented by one basis function, each composed of six Gaussians (“6”). The polarization functions (*) are present on “heavy atoms” – those beyond helium. Thus, H and He have a 1s orbital represented by an innerand an outer 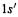basis function, making two basis functions. Carbon has a 1s function represented by six Gaussians, an inner 2s, and function, each composed of three Gaussians, and an outer and 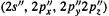function, each composed of one Gaussian, and six (not five) 3d functions, making a total of 15 basis functions. A 6-31G* calculation on uses 15 + 2 + 2 = 19 basis functions, and generates 19 MO’s. In the closed-shell species the eight electrons occupy four of these MO’s, so there are 15 unoccupied or virtual MO’s; compare this with a 3-21G calculation on (above) where there are a total of 13 MOs and nine virtual MOs. The 6-31G* basis, also often called 6-31G(d), is summarized in Fig. 5.13(d).

The 6-31G* is probably the most popular basis at present. It gives good geometries and, often, reasonable relative energies (section 5.5.2); however, there seems to be little evidence that it is, in general, much better than the basis for geometry optimizations. Since it is about 10 times as slow (Table 5.3) as the basis, the general preference for the 6-31G* for geometry optimizations may be due to its better relative energies (section 5.5.2). The basis does have certain geometry deficiencies compared to the 6-31G*, particularly its tendency to overzealously flatten nitrogen atoms (the N of aniline is wrongly predicted to be planar), and this, along with inferior relative energies and less consistency, may be responsible for its being neglected in favor of the 6-31 G* basis set [42]. The virtues of the and 6-31G* basis sets for geometry optimizations are discussed further in section 5.5.1. Note that the geometries and energies referred to here are those from HF-level calculations. PostHF (section 5.4) calculations, which can give significantly better geometries and much

226 Computational Chemistry

better relative energies (sections 5.5.1 and 5.5.2), require a basis set of at least the 6-31G* size for meaningful results.

The 6-31G* basis adds polarization functions only to so-called heavy atoms (those beyond helium). Sometimes it is helpful to have polarization functions on the hydrogens

the hydrogens are engaged in some special activity like hydrogen bonding or bridging [43]. In high-level calculations on hydrogen bonding or on boron hydrides, for example, polarization functions are placed on hydrogen. For calculations on and references to the hydrogen bonded water dimer, see section 5.4.3.

Diffuse functions

Core electrons or electrons engaged in bonding are relatively tightly bound to the molecular nuclear framework. Lone-pair electrons or electrons in a (previously) virtual orbital, are relatively loosely held, and are on the average at a larger distance from the nuclei than core or bonding electrons. These “expanded” electron clouds are found in molecules with heteroatoms, in anions, and in electronically excited molecules. To simulate well the behaviour of such species diffuse functions are used. These are Gaussian functions with small values of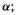this causes to fall off very slowly with the distance r from the nucleus, so that by giving enough weight to the coefficients of diffuse functions the SCF process can generate significant electron density at relatively large distances from the nucleus. Typically a basis set with diffuse functions has one such function, composed of a single Gaussian, for each valence atomic orbital of the “heavy atoms”. The 3-21 + G basis set for carbon for this element) is

13 basis functions

and the basis for carbon is

19 basis functions

Sometimes diffuse functions are added to hydrogen and helium as well as to the heavy atoms; such a basis set is indicated by + +. The 3-21 + +G and 6-31 + +G basis for

Ab initio calculations 227

hydrogen and helium is 1s

1s

1s+

3 basis functions

A 3-21++G calculation on would use 13 + 3 + 3 =19 basis functions, a 6-31 + +G* calculation 19 + 3 + 3 = 25 basis functions, and a 6-31 + +G** calculation 19 + 6 + 6 = 25 basis functions.

There is some disagreement over when diffuse functions should be used. Certainly most workers employ them routinely in studying anions and excited states, but not ordinary lone pair molecules (molecules with heteroatoms, like ethers and amines). A reasonable recommendation is to study with and without diffuse functions species representative of the problem at hand, for which experimental results are known, and see if these functions help. A paper by Warner [43] gives useful references and a good account of the efficacy of diffuse functions in treating certain molecules with heteroatoms.

Large basis sets

The is a small basis set and the 6-31G* and 6-31G** are moderate-size basis sets. Of those we have discussed, only the 6-31G* and 6-31G** with diffuse functions (6-31+G*, 6-31++G*, 6-31+G** and 6-31++G**) might be considered fairly large. A large basis set might have a doubly-split or even triply-split valence shell with d, p and f, and maybe even g, functions on at least the heavy atoms. An example of a large (but not very large) basis set is the 6-311G** (i.e. 6-311(d,p)) set. This is a split valence set with each valence orbital split into three shells, composed of three, one and one Gaussian, while the core orbitals are represented by one basis function composed of six Gaussians; each heavy atom also has five (not six in this case) 3d functions and each hydrogen and helium has three 2p functions. The 6-311G** basis for carbon is then

18 basis functions and for hydrogen

6 basis functions

Unequivocally large basis sets would be triply-split valence shell sets with d and f functions on heavy atoms and p functions on hydrogen. At the smaller end of such sets

Ab initio calculations 229

Note that all these large basis sets can be made still bigger by adding diffuse functions to heavy atoms (+) or to heavy atoms and hydrogen/helium (++). The number of basis functions on using some small, medium and large bases is summarized (C+H+H):

Large basis sets are used mainly for post-HF level (section 5.4) calculations, where the use of a basis smaller than the 6-31G* is essentially pointless. At the HF level the largest basis routinely used is the 6-31G* or 6-31G** (augmented if appropriate by diffuse functions), and postHF geometry optimizations are frequently done using the 6-31G* or 6-31G** basis too. Use of the larger bases (6-311G** and up) tends to be confined to single-point calculations on structures optimized with a smaller basis set (section 5.5.2). These are not firm rules: the high-accuracy CBS (complete basis set) methods (section 5.5.2) use as part of their procedure single-point HF (rather than postHF) level calculations with very large basis sets, and geometry optimizations with large basis sets were performed at both HF and post-HF levels in studies of the theoretically and experimentally challenging oxirene system [44].

Effective core potentials (pseudopotentials)

From about the third row (potassium to krypton) of the periodic table on the large number of electrons (19–36) has a considerable slowing effect on conventional ab initio calculations, because of the large number of two-electron repulsion integrals they engender. The usual way of avoiding this problem is to add to the Fock operator a one-electron operator that takes into account the effect of the core electrons on the valence electrons, which latter are still considered explicitly. This “average core effect” operator is called an effective core potential (ECP) or a pseudopotential. With a set of valence orbital basis functions optimized for use with it, it simulates the effect on the valence electrons ofthe atomic nuclei plus the core electrons. A distinction is sometimes made between an ECP and a pseudopotential, the latter term being used to mean any approach limited to the valence electrons, while ECP is sometimes used to designate a simplified pseudopotential corresponding to a function with fewer orbital nodes than the “correct” functions. However, the terms are often used interchangeably to designate a nuclei-plus-core electrons potential used with a set of valence functions, and that is what is meant here.

So far we have discussed nonrelativistic ab initio methods: they ignore those consequences of Einstein’s theory of relativity that are relevant to chemistry (section 4.2.3). These consequences arise in the special (rather than the general) theory, from the dependence of mass on velocity [45]. This dependence causes the masses of the inner electrons of heavy atoms to be significantly greater than the electron rest mass; since the Hamiltonian operator in the Schrödinger equation contains the electron mass (Eqs (5.36) and (5.37)), this change of mass should be taken into account. Relativistic effects in

230 Computational Chemistry

heavy-atom molecules affect geometries, energies, and other properties. Relativity is accounted for in the relativistic form of the Schrödinger equation, the Dirac equation (interestingly, Dirac thought his equation would not be relevant to chemistry [46]). This equation is not commonly used explicitly in molecular calculations, but is instead used to develop [47] relativistic effective core potentials (relativistic pseudopotentials). Relativistic effects begin to become significant for about third-row elements, i.e. those for which ECPs begin to be useful for speeding up calculations, so it makes sense to take relativistic effects into account in developing these potential operators and their basis functions, and indeed ECPs are generally relativistic. Such ECPs can give accurate results for molecules with third-row-plus atoms by simulating the relativistic mass increase. Comparing such a calculation on silver fluoride using the popular LANL2DZ basis set (a split valence basis) with a 3-21G* calculation, using Gaussian 94 for Windows [48] on a PentiumPro:

LANL2DZ basis, 31 basis functions, 1.9 min; Ag-F = 2.064 Å

basis, 48 basis functions, 2.6 min; Ag-F = 2.019 Å

The experimental bond length is 1.983 Å [49].

In this simple case there is no real advantage to the pseudopotential calculation (the 3-21G* geometry is actually better!), but for more challenging calculations on “very- heavy-atom” molecules, particularly transition metal molecules, ab initio calculations use pseudopotentials almost exclusively. A concise description of pseudopotential theory and specific relativistic effects on molecules, with several references, is given by Levine [50]. Reviews oriented toward transition metal molecules [51a,b] and the lanthanides [51c] have appeared, as well as detailed reviews of the more “technical” aspects of the theory [52].

Which basis set should I use ?

There are books of practical advice [1e,k,53] which help to provide a feel for the appropriateness of various basis sets. By reading the research literature one learns what approaches, including which basis sets, are being applied to a various problems, especially those related to the one’s research. This said, one should avoid simply assuming that the basis used in published work was the most appropriate one: in the absence of evidence to the contrary, one may suspect that it was either too small or unnecessarily big. Hehre [32] has shown that in many cases the use of very large bases is pointless; on the other hand some problems yield, if at all, only to very large basis sets (see below). A Goldilocks-like basis can rarely (except for calculations of a cursory or routine nature) be simply picked; rather, one homes in on an it, by experimenting. A rational approach in many cases might be to survey the territory first with a semiempirical method (chapter 6) or with the STO-3G basis and to use one of these to create input structures and input hessians (section 2.4) for higher-level calculations) then to move on to the basis or possibly the for a reasonable exploration of the problem. For a novel system for which there is no previous work to serve as a guide one should move up to larger basis sets and to post-HF methods (section 5.4), climbing the ladder of sophistication until reasonable convergence of at least qualitative results has been obtained. Janoschek has given an excellent survey indicating the reliability of ab initio