394 Computational Chemistry

Functional derivatives, which are akin to ordinary derivatives, are discussed by Parr and Yang [32] and outlined by Levine [33]. We need the derivative for the KS equations (7.23), and the exchange-correlation functional itself for the energy equation (7.21).

The KS equations (7.23) can be written as

The KS operator is defined by Eq. 7.23; The significance of these orbitals and energy levels is considered later, but we note here that in practice they can be interpreted in a similar way to the corresponding HF and extended Hückel entities. Pure DFT theory has no orbitals or wavefunctions; these were introduced by Kohn and Sham only as a way to turn Eq. (7.11) into a useful computational tool, but if we can interpret the KS orbitals and energies in some physically useful way, so much the better.

The KS energy equation (7.21) is exact: if we knew the densityfunction and the exchange-correlation energyfunctional it would give the exact energy. The HF energy equation (Eq. (5.17), on the other hand, is an approximation that does not treat electron correlation properly. Similar considerations hold for the KS and HF equations, derived from the energy equations by minimizing the energy with respect to orbitals: even in the basis set limit, the HF equations would not give the correct energy, but the KS equations would, if we knew the exact exchange-correlation energy functional. In wavefunction theory we know how to improve on HF-level results: by using perturbational or configuration interaction treatments of electron correlation (section 5.4), but in DFT theory there is as yet no systematic way of improving the exchange-correlation energy functional. It has been said [34] that “while solutions to the [HF equations] may be viewed as exact solutions to an approximate description, the [KS equations] are approximations to an exact description!"

7.2.3.3 Solving the KS equations

First let us review the steps in carrying out a HF calculation (sections 5.2.3.6b–e). We start with a guess of the basis function coefficients c (cf. Eqs (7.26)), because

the HF operator 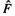involves the J and K integrals (section 5.2.3.6) which contain the wavefunction, and thus the c’s (the wavefunction is composed of the c’s and the basis functions). The operator is used with the basis functions to calculate the HF Fock

these are then used as a new guess to calculate a new F; the process continues till it converges satisfactorily on the c’s (i.e. the wavefunction) and the energy levels (which can be used to calculate the electronic energy); the procedure was shown in detail in section 5.2.3.6e.

Density Functional Calculations 395

The standard way of solving the KS eigenvalue equations, like that of solving the HF equations, which they resemble, is to expand the KS orbitals in terms of basis functions

This is exactly the same as was done with the HF orbitals in section 5.2.3.6a, and in fact the same basis functions are often used as in wavefunction theory, although as in all calculations designed to capture electron correlation, sets smaller than split-valence (section 5.3.3) should not be used; a popular basis in DFT calculations is the 6-31G*. Substituting the basis set expansion into the KS equations (7.23), (7.25) and multiplying by leads, as in section 5.2.3.6a, to m sets of equations, each set with m equations, which can all be subsumed into a single matrix equation analogous to the HF equation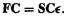 The key to solving the KS equations then becomes, as in the standard HF method, the calculation of Fock matrix elements and diagonalization of the matrix (section 5.2.3.6b). In a DFT calculation we start with a guess of the density 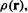because this is what we need to obtain an explicit expression for the KS Fock operator(Eqs (7.23), (7.25), (7.24)). This guess is usually a noninteracting atoms guess, obtained by summing the electron densities of the individual atoms of the molecule, at the molecular geometry. The KS Fock matrix elements are calculated and the KS Fock matrix is orthogonalized and diagonalized, etc., to give initial guesses of the c’s in the basis set expansion of Eq. (7.26) (and also initial values of the These c’s are used in Eq. (7.23) to calculate a better density function (the orbitals in Eq. (7.22) are composed of the c’s and the chosen basis set – Eq. (7.26)). This new density function is used to calculate improved matrix elements which in turn give improved c’s and then an improved density function, the iterative process being continued until the electron density etc. converge. The final density and KS orbitals are used to calculate the energy from Eq. (7.21).

The KS Fock matrix elements are integrals of the Fock operator over the basis functions. Because useful functional are so complicated, these integrals, specifically the integrals, unlike the corresponding ones in HF theory, cannot be solved analytically. The usual procedure is to approximate the integral by summing the inte-

grand in steps determined by a grid. For example, suppose we want to integrate from 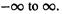This could be done approximately, using a grid of width

and summing from –2 to 2 (limits at which the function is small):

The integral is actually For a function f (x, y) the grid would define the steps in x and y and actually look like a grid or net, approximating the integral as a sum of the volumes of parallelepipeds, and for the DFT function f (x, y, z) the grid specifies the steps of x, y, and z. Clearly the finer the grid the more accurately the

Density Functional Calculations 397

The parameter is empirical; values of 1 to give reasonable results for atoms. For the place of the 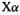method within the LDA and comparisons of atomic 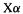calculations with KS LDA and with HF calculations, see Parr and Yang [36].

7.2.3.4b The local spin density approximation (LSDA)

Better results than with the LDA are obtained by an elaboration of the LDA in which

follow. This “unrestricted” LDA method (cf. UHF, section 5.2.3.6e) is called the local spin density approximation, LSDA, and has the advantages that it can handle systems with one or more unpaired electrons, like radicals, and systems in which electrons are becoming unpaired, such as molecules far from their equilibrium geometries; even for ordinary molecules it appears to be more forgiving toward the use of (necessarily)

and electron-distribution properties tend to be reasonably good, but (as with HF calculations) the dissociation energies are very poor, and uniform electron gas-type LSDA calculations appear to have been largely replaced by an approach that involves not just the electron density, but its gradient.

7.2.3.4c Gradient-corrected functionals and hybrid functionals

Gradient-corrected functionals

The electron density in an atom or molecule varies greatly from place to place, so it is not surprising that the uniform electron gas model has serious shortcomings. Most DFT calculations nowadays use exchange-correlation energyfunctionals that not only involve the LSDA, but also utilize both the electron density and its gradient or slope (first derivatives with respect to position). These functionals are called gradientcorrected, or said to use the generalized-gradient approximation (GGA). They are also called nonlocal functionals, in contrast to the older, local LDA and LSDA functionals.

The term nonlocal may refer to the fact that calculating the gradient of at a point amounts to sampling the value of an infinitesimal distance beyond the “local” point of the coordinates r, since the gradient is the change in over an infinitesimal distance divided by that distance (i.e. in a Taylor series expansion of a function about a point the first, second etc. terms represent sampling the function increasingly nonlocally [40]). Nevertheless, it has been suggested [41] that the term nonlocal be avoided in referring to gradient-corrected functionals.

The exchange-correlation energy functional can be written as the sum of an exchange-energy functional and a correlation-energy functional, both negative, i.e.

not surprising that gradient corrections have proved more effective when applied to the exchange-energy functional, and a major advance in practical DFT calculations was the introduction of the Becke 88 functional [43], a “new and greatly improved functional

398 Computational Chemistry

for the exchange energy” [44]. Another example of a gradient-corrected exchangeenergy functional is the Gill 1996 (G96) functional. Examples of gradient-corrected correlation-energy functionals are the Lee–Yang–Parr (LYP) and the Perdew 1986 (P86) functionals. All these functionals are commonly used with Gaussian-type (i.e. functions with basis functions for representing the KS orbitals (Eq. (7.26)). A calculation with B88 for LYP for and the 6-31G* basis set (section 5.3.3) would be designated as a B88LYP/6-31G* or B88LYP/6-31G* calculation (the Gaussian 98 program [45] performs this with the keyword BLYP/6-31G*). A calculation with B88 for and P86 for is called B88-P86 or B88P86 (BP86 in Gaussian 98). Other possible combinations of and basis set are G96LYP/6-31 + G* and G96P86/6-311G**. References to the basis sets in Gaussian are given in the Gaussian manual and the online help. Sometimes rather than the analytical functions that constitute the standard Gaussian basis sets, numerical basis sets are used. A numerical basis function is essentially a table ofthe values that an atomic orbital wavefunction has at many points around the nucleus, with empirical functions fitted to pass through these points. The empirical functions are used in calculations instead of the analytical Gaussian-type functions. One such basis set is the DN* basis [46], available in some versions of the program Spartan [47]. A calculation designated by Spartan as BP/DN* uses the B88 and P86 (above) functionals with the DN* numerical basis. BP/DN* calculations are said [48] to give results similar to those from BP86/6-311G* ( section 5.3.3) calculations, and results in section 7.3.2.2b support this. A numerical basis with polarization functions on hydrogen, designated DN**, is also available.

Hybrid functionals

Hybrid functionals augment the DFT exchange-correlation energy with a term calculated from HF theory. In HF theory, one expression for the electronic energy is Eq. (5.17)

where the sums are over n occupied spatial orbitals. If we remove the core energy (the first term, involving only electron kinetic energy and electron–nucleus attraction) and the coulomb potential energy (involving the coulomb integrals K) from this equation, we are left with the exchange energy, involving only the double sum of the exchange integrals J (section 5.2.3.2):

Substituting into Eq. (7.29) the KS orbitals, which are quite similar to the HF orbitals (section 7.3.5), gives an expression, based on KS orbitals, for the HF exchange energy:

Since the KS Slater determinant is an exact representation of the wavefunction of the noninteracting-electrons reference system, is the exact exchange energy for