
- •COMPUTATIONAL CHEMISTRY
- •CONTENTS
- •PREFACE
- •1.1 WHAT YOU CAN DO WITH COMPUTATIONAL CHEMISTRY
- •1.2 THE TOOLS OF COMPUTATIONAL CHEMISTRY
- •1.3 PUTTING IT ALL TOGETHER
- •1.4 THE PHILOSOPHY OF COMPUTATIONAL CHEMISTRY
- •1.5 SUMMARY OF CHAPTER 1
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •2.1 PERSPECTIVE
- •2.2 STATIONARY POINTS
- •2.3 THE BORN–OPPENHEIMER APPROXIMATION
- •2.4 GEOMETRY OPTIMIZATION
- •2.6 SYMMETRY
- •2.7 SUMMARY OF CHAPTER 2
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •3.1 PERSPECTIVE
- •3.2 THE BASIC PRINCIPLES OF MM
- •3.2.1 Developing a forcefield
- •3.2.2 Parameterizing a forcefield
- •3.2.3 A calculation using our forcefield
- •3.3 EXAMPLES OF THE USE OF MM
- •3.3.2 Geometries and energies of polymers
- •3.3.3 Geometries and energies of transition states
- •3.3.4 MM in organic synthesis
- •3.3.5 Molecular dynamics and Monte Carlo simulations
- •3.4 GEOMETRIES CALCULATED BY MM
- •3.5 FREQUENCIES CALCULATED BY MM
- •3.6 STRENGTHS AND WEAKNESSES OF MM
- •3.6.1 Strengths
- •3.6.2 Weaknesses
- •3.7 SUMMARY OF CHAPTER 3
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •4.1 PERSPECTIVE
- •4.2.1 The origins of quantum theory: blackbody radiation and the photoelectric effect
- •4.2.2 Radioactivity
- •4.2.3 Relativity
- •4.2.4 The nuclear atom
- •4.2.5 The Bohr atom
- •4.2.6 The wave mechanical atom and the Schrödinger equation
- •4.3.1 Introduction
- •4.3.2 Hybridization
- •4.3.3 Matrices and determinants
- •4.3.4 The simple Hückel method – theory
- •4.3.5 The simple Hückel method – applications
- •4.3.6 Strengths and weaknesses of the SHM
- •4.4.1 Theory
- •4.4.2 An illustration of the EHM: the protonated helium molecule
- •4.4.3 The extended Hückel method – applications
- •4.4.4 Strengths and weaknesses of the EHM
- •4.5 SUMMARY OF CHAPTER 4
- •REFERENCES
- •EASIER QUESTIONS
- •5.1 PERSPECTIVE
- •5.2.1 Preliminaries
- •5.2.2 The Hartree SCF method
- •5.2.3 The HF equations
- •5.2.3.1 Slater determinants
- •5.2.3.2 Calculating the atomic or molecular energy
- •5.2.3.3 The variation theorem (variation principle)
- •5.2.3.4 Minimizing the energy; the HF equations
- •5.2.3.5 The meaning of the HF equations
- •5.2.3.6a Deriving the Roothaan–Hall equations
- •5.3 BASIS SETS
- •5.3.1 Introduction
- •5.3.2 Gaussian functions; basis set preliminaries; direct SCF
- •5.3.3 Types of basis sets and their uses
- •5.4 POST-HF CALCULATIONS: ELECTRON CORRELATION
- •5.4.1 Electron correlation
- •5.4.3 The configuration interaction approach to electron correlation
- •5.5.1 Geometries
- •5.5.2 Energies
- •5.5.2.1 Energies: Preliminaries
- •5.5.2.2 Energies: calculating quantities relevant to thermodynamics and to kinetics
- •5.5.2.2a Thermodynamics; “direct” methods, isodesmic reactions
- •5.5.2.2b Thermodynamics; high-accuracy calculations
- •5.5.2.3 Thermodynamics; calculating heats of formation
- •5.5.2.3a Kinetics; calculating reaction rates
- •5.5.2.3b Energies: concluding remarks
- •5.5.3 Frequencies
- •Dipole moments
- •Charges and bond orders
- •Electrostatic potential
- •Atoms-in-molecules
- •5.5.5 Miscellaneous properties – UV and NMR spectra, ionization energies, and electron affinities
- •5.5.6 Visualization
- •5.6 STRENGTHS AND WEAKNESSES OF AB INITIO CALCULATIONS
- •5.7 SUMMARY OF CHAPTER 5
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •6.1 PERSPECTIVE
- •6.2 THE BASIC PRINCIPLES OF SCF SE METHODS
- •6.2.1 Preliminaries
- •6.2.2 The Pariser-Parr-Pople (PPP) method
- •6.2.3 The complete neglect of differential overlap (CNDO) method
- •6.2.4 The intermediate neglect of differential overlap (INDO) method
- •6.2.5 The neglect of diatomic differential overlap (NDDO) method
- •6.2.5.2 Heats of formation from SE electronic energies
- •6.2.5.3 MNDO
- •6.2.5.7 Inclusion of d orbitals: MNDO/d and PM3t; explicit electron correlation: MNDOC
- •6.3 APPLICATIONS OF SE METHODS
- •6.3.1 Geometries
- •6.3.2 Energies
- •6.3.2.1 Energies: preliminaries
- •6.3.2.2 Energies: calculating quantities relevant to thermodynamics and kinetics
- •6.3.3 Frequencies
- •6.3.4 Properties arising from electron distribution: dipole moments, charges, bond orders
- •6.3.5 Miscellaneous properties – UV spectra, ionization energies, and electron affinities
- •6.3.6 Visualization
- •6.3.7 Some general remarks
- •6.4 STRENGTHS AND WEAKNESSES OF SE METHODS
- •6.5 SUMMARY OF CHAPTER 6
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •7.1 PERSPECTIVE
- •7.2 THE BASIC PRINCIPLES OF DENSITY FUNCTIONAL THEORY
- •7.2.1 Preliminaries
- •7.2.2 Forerunners to current DFT methods
- •7.2.3.1 Functionals: The Hohenberg–Kohn theorems
- •7.2.3.2 The Kohn–Sham energy and the KS equations
- •7.2.3.3 Solving the KS equations
- •7.2.3.4a The local density approximation (LDA)
- •7.2.3.4b The local spin density approximation (LSDA)
- •7.2.3.4c Gradient-corrected functionals and hybrid functionals
- •7.3 APPLICATIONS OF DENSITY FUNCTIONAL THEORY
- •7.3.1 Geometries
- •7.3.2 Energies
- •7.3.2.1 Energies: preliminaries
- •7.3.2.2 Energies: calculating quantities relevant to thermodynamics and kinetics
- •7.3.2.2a Thermodynamics
- •7.3.2.2b Kinetics
- •7.3.3 Frequencies
- •7.3.6 Visualization
- •7.4 STRENGTHS AND WEAKNESSES OF DFT
- •7.5 SUMMARY OF CHAPTER 7
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •8.1 FROM THE LITERATURE
- •8.1.1.1 Oxirene
- •8.1.1.2 Nitrogen pentafluoride
- •8.1.1.3 Pyramidane
- •8.1.1.4 Beyond dinitrogen
- •8.1.2 Mechanisms
- •8.1.2.1 The Diels–Alder reaction
- •8.1.2.2 Abstraction of H from amino acids by the OH radical
- •8.1.3 Concepts
- •8.1.3.1 Resonance vs. inductive effects
- •8.1.3.2 Homoaromaticity
- •8.2 TO THE LITERATURE
- •8.2.1 Books
- •8.2.2 The Worldwide Web
- •8.3 SOFTWARE AND HARDWARE
- •8.3.1 Software
- •8.3.2 Hardware
- •8.3.3 Postscript
- •REFERENCES
- •INDEX
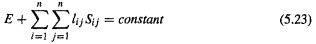
Ab initio calculations 171
the smallest closed-shell system in which K integrals arise. A detailed exposition of the significance of the HF integrals is given by Dewar [13]. Note that outside the nucleus the only significant forces in atoms and molecules are electrostatic; there are no vague “quantum-mechanical forces” in chemistry [14]. Chemical reactions involve the shuffling of atomic nuclei under the influence of the electromagnetic force.
5.2.3.3 The variation theorem (variation principle)
The energy calculated from Eq. (5.14) is the expectation value of the energy operator  i.e. the expectation value of the Hamiltonian operator. In quantum mechanics an integral of a wavefunction “over” an operator, as E in Eq. (5.14) is an integral of
i.e. the expectation value of the Hamiltonian operator. In quantum mechanics an integral of a wavefunction “over” an operator, as E in Eq. (5.14) is an integral of  over
over  is the expectation value of that operator. The expectation value is the value (strictly, the quantum-mechanical average value) of the physical quantity represented by the operator. Every “observable”, i.e. every measurable property of a system, has a quantum mechanical operator from which the property could be calculated, at least in principle, by integrating the wavefunction over the operator. The expectation value of the energy operator
is the expectation value of that operator. The expectation value is the value (strictly, the quantum-mechanical average value) of the physical quantity represented by the operator. Every “observable”, i.e. every measurable property of a system, has a quantum mechanical operator from which the property could be calculated, at least in principle, by integrating the wavefunction over the operator. The expectation value of the energy operator  is the energy of the molecule (or atom). Of course this energy will be the exact, true energy of the molecule only if the wavefunction
is the energy of the molecule (or atom). Of course this energy will be the exact, true energy of the molecule only if the wavefunction  and the Hamiltonian
and the Hamiltonian are exact. The variation theorem states that the energy calculated from Eq. (5.14) must be greater than or equal to the true ground-state energy ofthe molecule.
are exact. The variation theorem states that the energy calculated from Eq. (5.14) must be greater than or equal to the true ground-state energy ofthe molecule.
The theorem [15] (it can be stated more rigorously, specifying that  must be timeindependent and
must be timeindependent and  must be normalized and well-behaved) is very important in quantum chemistry: it assures us that any ground state (we examine electronic ground states much more frequently than we do excited states) energy we calculate “variationally” (i.e. using Eq. (5.14)) must be greater than or equal to the true energy of the molecule. In practice, any molecular wavefunction we insert into Eq. (5.14) is always only an approximation to the true wavefunction and so the variationally calculated molecular energy will always be greater than the true energy. The HF energy is variational (the method starts with Eq. (5.14)) so the variation theorem gives us at least some indication of the true energy and of how good our wavefunction is: the correct energy always lies below any calculated by the HF method, and the better the wavefunction, the lower the calculated energy. The HF energy actually levels off at a value above the true energy as the HF wavefunction, based on a Slater determinant, is improved; this is discussed in section 5.5, in connection with post-HF methods.
must be normalized and well-behaved) is very important in quantum chemistry: it assures us that any ground state (we examine electronic ground states much more frequently than we do excited states) energy we calculate “variationally” (i.e. using Eq. (5.14)) must be greater than or equal to the true energy of the molecule. In practice, any molecular wavefunction we insert into Eq. (5.14) is always only an approximation to the true wavefunction and so the variationally calculated molecular energy will always be greater than the true energy. The HF energy is variational (the method starts with Eq. (5.14)) so the variation theorem gives us at least some indication of the true energy and of how good our wavefunction is: the correct energy always lies below any calculated by the HF method, and the better the wavefunction, the lower the calculated energy. The HF energy actually levels off at a value above the true energy as the HF wavefunction, based on a Slater determinant, is improved; this is discussed in section 5.5, in connection with post-HF methods.
5.2.3.4Minimizing the energy; the HF equations
The HF equations are obtained from Eq. (5.17) by minimizing the energy with respect to the atomic or molecular orbitals  The minimization is carried out with the constraint that the orbitals remain orthonormal, for orthonormality was imposed in deriving Eq. (5.17). Minimizing a function subject to a constraint can be done using the method of undetermined Lagrangian multipliers [16]. For orthonormality the overlap integrals S must be constants
The minimization is carried out with the constraint that the orbitals remain orthonormal, for orthonormality was imposed in deriving Eq. (5.17). Minimizing a function subject to a constraint can be done using the method of undetermined Lagrangian multipliers [16]. For orthonormality the overlap integrals S must be constants  and at the minimum the energy is constant
and at the minimum the energy is constant  Thus at
Thus at  any linear combination of E and
any linear combination of E and  is constant:
is constant:

172 Computational Chemistry
where  are the Lagrangian multipliers; we do not know what they are, physically, yet (they are “undetermined”). Differentiating with respect to the
are the Lagrangian multipliers; we do not know what they are, physically, yet (they are “undetermined”). Differentiating with respect to the  of the S’s:
of the S’s:
Substituting the expression for E from Eqs (5.17) into (5.24) we get
Note that this procedure of minimizing the energy with respect to the molecular orbitals  is somewhat analogous to the minimization of energy with respect to the atomic orbital coefficients c in the less rigorous procedure which gave the Hückel secular equations in section 4.3.3. It is also somewhat similar to finding a relative minimum on a PES (section 2.4), but with energy in that case being varied with respect to geometry. Since the procedure starts with Eq. (5.14) and varies the MO’s to find the minimum value of E, it is called the variation method; the variation theorem (section 5.2.3.3) assures us that the energy we calculate from the results will be greater than or equal to the true energy.
is somewhat analogous to the minimization of energy with respect to the atomic orbital coefficients c in the less rigorous procedure which gave the Hückel secular equations in section 4.3.3. It is also somewhat similar to finding a relative minimum on a PES (section 2.4), but with energy in that case being varied with respect to geometry. Since the procedure starts with Eq. (5.14) and varies the MO’s to find the minimum value of E, it is called the variation method; the variation theorem (section 5.2.3.3) assures us that the energy we calculate from the results will be greater than or equal to the true energy.
From the definitions of

 and
and 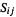 we get
we get
where
and
and similarly for |
and |

Ab initio calculations 173
Using for dH, dJ, dK and dS the expressions in Eqs (5.26), (5.27), (5.28) and (5.31), Eq. (5.25) becomes
Since the MOs can be varied independently, and the expression on the left side is zero, both parts of Eq. (5.32) (the part shown and the complex conjugate) equal zero. It can be shown that a consequence of
is that
i.e.
Equation (5.34) can be written as:
where  is the Fock operator:
is the Fock operator:
We want an eigenvalue equation because (cf. section 4.3.3) we hope to be able to use the matrix form of a series of such equations to invoke matrix diagonalization to get eigenvalues and eigenvectors. Equation (5.35) is not quite an eigenvalue equation, because it is not of the form Operation on function = k × function, but rather Operation on function = sum of (k × functions). However, by transforming the molecular orbitals

174 Computational Chemistry
 to a new set the equation can be put in eigenvalue form (with a caveat, as we shall see). Equation (5.35) represents a system of equations
to a new set the equation can be put in eigenvalue form (with a caveat, as we shall see). Equation (5.35) represents a system of equations
There are n spatial orbitals  since we are considering a system of 2n electrons and each orbital holds two electrons. The 1 in parentheses on each orbital emphasizes that each of these n equations is a one-electron equation, dealing with the same electron (we could have used a 2 or a 3, etc.), i.e. the Fock operator (Eq. 5.36) is a one-electron operator, unlike the general electronic Hamiltonian operator of Eq. (5.15), which is a multi-electron operator (a 2n electron operator for our specific case). The Fock operator acts on a total of n spatial orbitals, the
since we are considering a system of 2n electrons and each orbital holds two electrons. The 1 in parentheses on each orbital emphasizes that each of these n equations is a one-electron equation, dealing with the same electron (we could have used a 2 or a 3, etc.), i.e. the Fock operator (Eq. 5.36) is a one-electron operator, unlike the general electronic Hamiltonian operator of Eq. (5.15), which is a multi-electron operator (a 2n electron operator for our specific case). The Fock operator acts on a total of n spatial orbitals, the

 in Eq. (5.35).
in Eq. (5.35).
The series of equations (5.37) can be written as the single matrix equation (cf. Eq. (4.50))
i.e.
In Eqs (5.37), each equation will be of the form  which is what we want, if all the
which is what we want, if all the  except for i= j (e.g. in the first equation
except for i= j (e.g. in the first equation  if the only nonzero
if the only nonzero 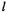 is
is  ). This will be the case if in Eq. (5.39) L is a diagonal matrix. It can be shown that L is diagonalizable (section 4.3.3), i.e. there exist matrices P,
). This will be the case if in Eq. (5.39) L is a diagonal matrix. It can be shown that L is diagonalizable (section 4.3.3), i.e. there exist matrices P,  and a diagonal matrix
and a diagonal matrix such that
such that
Substituting L from Eqs (5.40) into (5.39):
Multiplying on the left by  and on the right by P we get
and on the right by P we get
which, since  can be written
can be written

Ab initio calculations 175
where
We may as well remove the  factor by incorporating it into
factor by incorporating it into  and we can omit the prime from
and we can omit the prime from 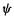 (we could have started the derivation using primes on the
(we could have started the derivation using primes on the 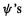 then written
then written for Eq. (5.43)). Equation (5.42) then becomes (anticipating the soon-to-be-apparent fact that the diagonal matrix is an energy-level matrix)
for Eq. (5.43)). Equation (5.42) then becomes (anticipating the soon-to-be-apparent fact that the diagonal matrix is an energy-level matrix)
where
Equation (5.44) is the compact form of (cf. Eq. (5.38)). Thus
where the superfluous double subscripts on the  have been replaced by single ones. Equations (5.44/5.46) are the matrix form of the system of equations
have been replaced by single ones. Equations (5.44/5.46) are the matrix form of the system of equations
These Eqs (5.47) are the HF equations (the matrix form is Eqs (5.44) or (5.46)). By analogy with the Schrödinger equation  we see that they show that the Fock operator acting on a one-electron wavefunction (an atomic or molecular orbital) generates an energy value times the wavefunction. Thus the Lagrangian multipliers
we see that they show that the Fock operator acting on a one-electron wavefunction (an atomic or molecular orbital) generates an energy value times the wavefunction. Thus the Lagrangian multipliers turned out to be (with the
turned out to be (with the 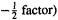 the energy values associated with the orbitals
the energy values associated with the orbitals  Unlike the Schrödinger equation the HF equations are not quite eigenvalue equations (although they are closer to this ideal than is Eq. (5.35)), because in
Unlike the Schrödinger equation the HF equations are not quite eigenvalue equations (although they are closer to this ideal than is Eq. (5.35)), because in  the Fock operator
the Fock operator  is itself dependent on
is itself dependent on  in a true eigenvalue equation the operator can be written down without reference to the function on which it acts. The significance of the HF equations is discussed in the next section.
in a true eigenvalue equation the operator can be written down without reference to the function on which it acts. The significance of the HF equations is discussed in the next section.
