86 Computational Chemistry

the photon, and is the kinetic energy of the free electron. Rearranging Eq. (4.5):

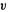Thus a plot of the kinetic energies of the electrons vs. the frequency of the light should be a straight line of positive slope (h; this is one way to find Planck’s

Planck’s explanation of the blackbody radiation curves (1900 [4]) and Einstein’s explanation of the facts of the photoelectric effect (1905 [7]) indicated that the flow of energy in physical processes did not take place continuously, as had been believed, but rather jerkily, in discrete jumps, quantum by quantum. The contributions of Planck and Einstein were the signal developments marking the birth of quantum theory and the transition from classical to modern physics.

4.2.2 Radioactivity

Brief mention of radioactivity is in order because it, along with quantum mechanics and relativity, transformed classical into modern physics. Radioactivity was discovered by Becquerel in 1896. However, an understanding of how materials like uranium and radium could emit, over the years, a million times more energy than would be permitted by chemical reactions, had to await Einstein’s special theory of relativity (section 4.2.3), which showed that a tiny, unnoticeable decrease in mass represented the release of a large amount of energy.

Introduction to Quantum Mechanics 87

4.2.3 Relativity

Relativity is relevant to computational chemistry because it must often be explicitly taken into account in accurate calculations involving atoms heavier than about chlorine or bromine (see below) and because, strictly speaking, the Schrödinger equation, the fundamental equation of quantum chemistry, is an approximation to a relativistic equation, the Dirac6 equation.

Relativity was discovered in by Einstein in 1905, when he formulated the special theory of relativity, which deals with nonaccelerated motion in the absence of significant gravitational fields (general relativity, published by Einstein in 1915, is concerned with accelerated motion and gravitation). Special relativity predicted a relationship between mass and energy, the famous equation and, of more direct relevance to computational chemistry, showed that the mass of a particle increases with its velocity, dramatically so near the velocity of light. In heavier elements the inner electrons are moving at a significant fraction of the speed of light, and the relativistic increase in their masses affects the chemistry of these elements (actually, some physicists do not like to think in terms of rest mass and relativistic mass, but that is a controversy that need not concern us here). In computational chemistry relativistic effects on electrons are usually accounted for by what are called effective core potentials or pseudopotentials (section 5.3.3).

4.2.4 The nuclear atom

The “nuclear atom” is the picture of the atom as a positive nucleus surrounded by negative electrons. Although the idea of atoms in speculative philosophy goes back to at least the time of Democritus,7 the atom as the basis of a scientifically credible theory emerges only in nineteenth century, with the rationalization by Dalton8 in 1808 of the law of definite proportions. Nevertheless, atoms were regarded by many scientists of the positivist school of Ernst Mach as being at best a convenient hypothesis, despite the success of the atomistic Maxwell-Boltzmann9 kinetic theory of gases and it was not until 1908, when Perrin’s10 experiments confirmed Einstein’s atomistic analysis of

6 Paul Adrien Maurice Dirac, born Bristol, England, 1902. Ph.D. Cambridge, 1926. Professor, Cambridge, Dublin Institute for Advanced Studies, University of Miami, Florida State University. Nobel prize in physics 1933 (shared with Schrödinger). Known for his mathematical elegance, for connecting relativity with quantum theory, and for predicting the existence of the positron. Died Tallahassee, Florida, 1984.

7 Democritus, Greek philosopher, born Abdera, Thrace (the eastern Balkans) ca. 470 B.C. Died ca. 370 B.C.

8John Dalton, born Eaglesfield, England, 1766. Considered the founder of quantitative chemical atomic theory: law of definite proportions, pioneered determination of atomic weights. Cofounder of British Association for the Advancement of Science. Died Manchester, England, 1844.

9 Ludwig Boltzmann, born Vienna 1844. Ph.D. Vienna. Professor Graz, Vienna. Developed the kinetic theory of gases independently of Maxwell (viz., Boltzmann constant’s, k). Firm supporter of the atomic theory in opposition to Mach and Ostwald, helped develop concept of entropy (S). Died Duino, Austria (now in Italy), 1906 (suicide incurred by depression). Inscribed on gravestone:

10 Jean Perrin, born Lille, France, 1870. Ph.D. École Normal Supérieure, Paris. Professor University of Paris. Nobel prize in physics 1923. Died New York, 1942.

Introduction to Quantum Mechanics 89

There is another thread to the development of the concept of the atom as a composite of subatomic particles. The enhanced effect of electrolytes (solutes that provide an electrically conducting solutions) on boiling and freezing points and on the osmotic pressure of solutions led Arrhenius14 in 1884 to propose that these substances exist in water as atoms or groups of atoms with an electric charge. Thus sodium chloride in solution would not, as was generally held, exist as NaCl molecules but rather as an a positive sodium “atom” and a negative chlorine “atom”; the presence of two particles instead of the expected one accounted for the enhanced effects. The ability of atoms to lose or gain charge hinted at the existence of some kind of subatomic structure, and although the theory was not warmly received (Arrhenius was almost failed on his Ph.D. exam), the confirmation by Thomson (ca. 1900) that the atom contains electrons made acceptable the concept of charged atoms with chemical properties quite different from those of the neutral ones. Arrhenius’ was awarded the Nobel prize for his Ph.D. work.

4.2.5 The Bohr atom

The nuclear atom as formulated by Rutherford faced a serious problem: the electrons orbit the nucleus like planets orbiting the Sun. An object engaged in circular (or elliptical) motion experiences an acceleration because its direction is changing and thus its velocity, which unlike speed is a vector, is also changing. An electron in circular motion about a nucleus would experience an acceleration toward the nucleus, and since from Maxwell’s equations of electromagnetism an accelerated electric charge radiates away energy, the electron should lose energy by spiralling in toward the nucleus, ending up there, with no kinetic and potential energy; calculations show this should happen in a fraction of a second [8].

A way out of this dilemma was suggested by Bohr15 in 1913 [9,10]. He retained the classical picture of electrons orbiting the nucleus in accord with Newton’s laws, but subject to the constraint that the angular momentum of an electron must be an integral multiple of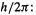

where m is the electron mass, is the electron velocity, r is the radius of electron orbit, and h is the Planck’s constant. Equation (4.7) is the Bohr postulate, that electrons can defy Maxwell’s laws provided they occupy an orbit whose angular momentum (i.e. an orbit of appropriate radius) satisfies Eq. (4.7). The Bohr postulate is not based on a whim, as most textbooks imply, but rather follows from: (1) the Plank equation Eq. (4.3), and (2) starting with an orbit of large radius such that the motion is essentially linear and classical physics applies, as no acceleration is involved, then extrapolating

14Svante Arrhenius, born near Uppsala, Sweden, 1859. Ph.D. University of Stockholm. Nobel prize in chemistry 1903. Professor Stockholm. Died Stockholm 1927.

15Niels Bohr, born Copenhagen, 1885. Ph.D. University of Copenhagen. Professor, University of Copenhagen. Nobel prize in physics 1922. Founder of the “Copenhagen school” interpretation of quantum theory. Died Copenhagen, 1962.

90 Computational Chemistry

to small-radius orbits. The fading of quantum-mechanical equations into their classical analogues as macroscopic conditions are approached is called the correspondence principle [11].

Using the postulate of Eq. (4.7) and classical physics, Bohr derived an equation for the energy of an orbiting electron in a one-electron atom (a hydrogen-like atom, H or 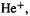etc.) in terms of the charge on the nucleus and some constants of nature. Starting

with the total energy of the electron as the sum of its kinetic and potential energies:

where Z is the nuclear charge (1 for H, 2 for He, etc.), e is the charge on the electron, is the permitivity of the vacuum. Using force = mass × acceleration:

i.e.

So from Eq. (4.8)

From Eqs (4.7) and (4.10):

So from Eqs (4.11) and (4.12):

Equation (4.13) expresses the total (kinetic plus potential) energy of the electron of a hydrogen-like atom in terms of four fundamental quantities of our universe: electron charge, electron mass, the permittivity of empty space, and Planck’s constant. From Eq. (4.13) the energy change involved in emission or absorption of light by a hydrogenlike atom is simply

where is the energy of a state characterized by quantum number minus the energy of a state characterized by quantum number Note that from Eq. (4.13) the total energy increases (becomes less negative) as n increases (= 1,2, 3,...), so higherenergy states are associated with higher quantum numbers n and corresponds to absorption of energy and to emission of energy. The Planck relation between the amount of radiant energy absorbed or emitted and its frequency 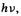Eq. (4.3)), Eq. (4.14) enables one to calculate the frequencies of spectroscopic absorption and emission lines for hydrogen-like atoms. The agreement with experiment is excellent, and the same is true too for the calculated ionization energies of hydrogenlike atoms for in Eq. (4.14)).