6.3.2 Energies

362 Computational Chemistry

(room temperature, 298 K) heats of formation. This is in distinct contrast to ab initio calculations, which give (the negative of) the energy for total dissociation of the molecule into nuclei and electrons, starting from a hypothetical zero-vibrational energy state or from the 0 K state with ZPE included (section 5.5.2.1). Ab initio methods can be made to provide heats of formation, by slightly roundabout methods (section 5.5.2.2c). The errors in SE heats of formation might at first strike one as being very large; thus for the common diatomic molecules, which by definition have standard heats of forma-

–22.0/ + 20.6. An extensive compilation of AM1 and PM3 heats of formation (which corrects errors in earlier values) [44] gave for 657 normal-valent compounds these average errors for the absolute deviations 53/33; for 106 hypervalent compounds 348 (sic)/57. These results are not as bad as they may at first seem if we note that (1) the heats of formation of organic compounds are commonly in the region of (2) often we are interested in trends, which are more likely to be qualitatively right than actual numbers are to be quantitatively accurate, and (3) usually chemists are concerned with energy differences, i.e. relative energies (below). AM1 heats of formation for hypervalent compounds (above and Ref. [47]) appear to be distinctly inferior to those from PM3. Thiel has compared MNDO, AM1, PM3, and MNDO/d heats of formation with those from some ab initio methods [64].

The discussion of enthalpy, free energy, and reaction and activation energies in section 5.5.2.1 applies to SE calculations too. Now let’s retrace some of the calculations of chapter 5, using AM1 and PM3 rather than ab initio methods.

6.3.2.2Energies: calculating quantities relevant to thermodynamics and kinetics

We are usually interested in relative energies. An ab initio energy difference (for isomers, or isomeric systems like reactants cf. products) represents a 0 K energy difference, i.e. a 0 K enthalpy difference, whereas a semiempirical (AM1 or PM3) energy difference represents a room temperature enthalpy difference; thus even if the ab initio and SE calculations both had negligible errors, they would not be expected to give exactly the same relative energy, unless the 0–298 K enthalpy change on both sides of the equation cancelled. A typical change in heat of formation is shown by methanol; the (ab initio calculated) heats of formation of methanol at 0 and 298 K are –195.9 and respectively (section 5.5.2.2c). This change of is small compared to the errors in SE and many ab initio calculations, so discrepancies between energy changes calculated by the two approaches must be due to factors other than the 0–298 K enthalpy change. The errors in heats of formation cannot be counted on to consistently cancel when we subtract to obtain relative energies, and because of the quite large errors in the heats of formation (53 and for AM 1 and PM3, for a large sample of “normal compounds”; section 6.6.2.1) errors of about should not be uncommon, although much smaller errors are often obtained. Consider the relative energies of (Z)- and (E)-2-butene (Fig. 5.24). The HF/3-21G energy difference, corrected for ZPE (although in this case the ZPE is practically the same for both isomers) is (Z) – (E) = –155.12709 – (–155.13033)h = 0.00324 h =

Semiempirical Calculations 363

AM1 calculations (ZPE is not considered here, since as explained in section 6.2.5.2, this is taken into account in the parameterization) give 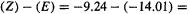The experimental heats of formation (298 K, gas phase) are i.e. [65].

The comparison by Schröder and Thiel [62] (section 6.3.1) of SE (MNDO and MNDOC) and ab initio geometries and energies concluded that the SE methods usually overestimate activation energies. Of 21 activation energies (Table IV in Ref. [62], entries I, K, W omitted), MNDO overestimated (compared with “best” correlated

significantly better than MNDO, and it is probably better than AM1 for this purpose, since, like MNDO but unlike MNDOC, AM1 does not explicitly take into account electron correlation, which can be important for activation energies. For these 21 reactions, restricted Hartree–Fock calculations overestimated 18 activation energies and

(uncorrelated) calculations for activation energies. Correlated-level ab initio calculations, however, appear to be superior to MNDOC; in particular, MNDOC predicts substantial barriers for isomerization of carbenes by hydrogen migration. Other work showed that AM 1 greatly overestimates the barrier for decomposition or rearrangement of some highly reactive species [66].

Some SE reaction energies and relative energies of isomers are given in Table 6.3; these are analogous to the ab initio results in Table 5.9. These calculations suggest that, like the Hartree–Fock-level calculations of Table 5.9, AM1 and PM3 can give useful, although sometimes only rough, indications of the magnitude of energy differences. Further information on the reliability of these methods is provided by the calculations for the four reactions summarized in Fig. 6.3, which were discussed in section 6.3.1 in connection with geometries. Fig. 6.4, based on the energies in Fig. 6.3, makes these results clear. In all four cases the SE methods give the relative energies of the products semiquantitatively; the worst deviation from experiment is for the PM3 relative energy

best (and in the other two cases, the MP2 energies are the best); however, this is likely to be due to an atypical cancellation of errors. The transition state relative energies are best-approximated in one case 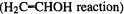by AM1 and PM3, and in the other three cases by MP2; for these three latter reactions the SE relative energies are considerably higher than the experimental and MP values, which accords with other work mentioned above [62,66].

From the available information, then, we can conclude that SE heats of formation and reaction energies (reactant cf. product) are semiquantitatively reliable. Activation energies (reactant cf. transition state) are usually considerably overestimated by AM1 and PM3, but are handled better by MNDOC, which actually gives results somewhat