316 Computational Chemistry

energies, implying that molecules will not accept electrons to form anions (i.e. that they have negative EAs), which is often false. Koopmans’ theorem works because of a cancellation of errors in the IE case (which actually leads to modest overestimation of the IE) but not for EAs. Errors arise from approximate treatment of electron correlation, and from the fact that when an electron is removed from or added to a molecule electronic relaxation (not to be confused with geometry relaxation) occurs. A further problem for EAs is that the procedure for minimizing the energies of MOs (section 5.2.3.4) gives, within the limits of the HF procedure, the best occupied, but not virtual, MOs.

Some calculated and experimental IEs are given in Table 5.21, based on the raw data in Table 5.22. The calculations (experimental data are sparse) indicate vertical IEs to be indeed slightly (about 0.2 eV) higher than adiabatic. The HF/6-31G* 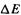values underestimate the IE by about 1–1.5eV while MP2(FC)/6-31G* values underestimate it by only about 0.1–0.4eV (others have reported them to be generally too low by 0.3–0.7 eV [183]). The Koopmans’ theorem (-HOMO) energies for both the HF and MP2 level calculations are about 1–1.5eV too high. Electron affinities (which seem to be of less interest than ionization energies) can be calculated as the energy difference between the neutral molecule and its anion. High-accuracy IEs and EAs can be calculated by the G2 (or a variation like G2(MP2)) method or one of the CBS methods [86,184,185] (section 5.5.2.2b), although the convenient procedures implemented for these methods in the Gaussian 94 and 98 programs do not allow calculation of vertical energies since the geometry of the ion will be automatically optimized.

5.5.6 Visualization

Modern computer graphics have given visualization, the pictorial presentation of the results of calculations, a very important place in science. Not only in chemistry, but in physics, aerodynamics, meteorology, and even mathematics, the remarkable ability of the human mind to process visual information is being utilized [186]. Gone are the days when it was de rigeur to pore over tables of numbers to comprehend the factors at work in a system, whether it be a galaxy, a supersonic airliner, a thunderstorm, or a novel mathematical entity. We will briefly examine the role of computer graphics

Ab initio calculations 317

in computational chemistry, limiting ourselves to molecular vibrations, van der Waals surfaces, charge distribution, and molecular orbitals.

Molecular vibrations

Animation of normal-mode frequencies usually readily enables one to ascribe a band in the calculated vibrational (i.e. IR) spectrum to a particular molecular motion (a stretching, bending, or torsional mode, involving particular atoms). It sometimes requires a little ingenuity to describe clearly the motion involved, but animation is far superior

318 Computational Chemistry

to trying to discern the motion from the printed direction vectors (section 2.5; these show the extent of motion in the x, y, and z directions), which are supplied by some programs. Useful, however, are the visualized direction vectors that some programs, e.g. GaussView [187], can attach to a picture of the molecule, catching the vibration in the act so to speak.

Animating vibrations is useful not only for predicting or interpreting an IR spectrum, but can sometimes also help in geometry optimizations. Suppose we wish to locate computationally the intermediate through which the chair conformers of cyclohexane interconvert 1 Fig. 5.45). This reaction, although degenerate, can be studied by NMR spectroscopy [188]. One might surmise that the intermediate is the boat conformation 2, but a geometry optimization and frequencies calculation on this structure (note that in a quantum mechanical calculation, whether ab initio or otherwise, the input symmetry is normally preserved) followed by animation of the vibrations, shows otherwise. There is one imaginary vibration (section 2.5), and the transition state wants to escape from its saddle point by twisting to a structure 3, called the twist or twist-boat, which latter is the true intermediate. The enantiomeric twist structures

minimum. Similarly, if one obtains a second-order saddle point (one kind of hilltop), animation of the two imaginary frequencies often indicates what the species seeks to do to escape from the hilltop to a become a first-order saddle point (a transition state) or

Ab initio calculations 319

a minimum, and it often possible to obtain the desired transition state or minimum by altering the shape of the input structure so that it has the symmetry and approximates the shape of the desired structure. An example is provided by cyclopropylamine (Fig. 5.46) [189]; the structure 1 is a hilltop at the B3LYP/6-31G* level (chapter 7), whose two imaginary frequencies indicate that it wants to undergo nitrogen pyramidalization and rotation about the C–N bond to form the other four conformations shown.

Electrostatic potential

Electrostatic potential, the net electrostatic potential energy (roughly, the charge) due to nuclei and electrons was mentioned in section 5.5.4 in connection with calculation of atom charges. The ESP can be displayed (visualized) by color-coding it onto the van der Waals surface, by displaying it as a surface itself, or by showing it with contour lines on a slice through the molecule; the three possibilities are shown for the water molecule

320 Computational Chemistry

in Fig. 5.47. Color-coding (mapping) the ESP onto the surface of the molecule, (c), enables one to see how an approaching reagent would perceive the charge distribution. Showing the ESP as a surface residing in the region of space where the net charge is negative, (b), gives a very useful picture of those parts of a molecule where the electrostatic effect of the electrons wins out over that of the nuclei; this is a particularly good way of seeing the presence of lone pairs, as Fig. 5.48, also, makes clear. Note that in Fig. 5.47(c) and (b) (mapping of the ESP on the van der Walls surface and depicting the ESP itself as a surface) the lone pairs do not stick out like rabbit ears [190]. This is because as electron density which can be ascribed to one orbital falls off, that due to another increases: there is no “electron hole” between the two lone pairs (for the same reason the electron density cross section through a double bond is elliptical and through a triple bond circular; see section 4.3.2). Showing the ESP as a surface made clear that the remarkable cycloalkane pyramidane [191] has a lone pair, like the carbene (Fig. 5.48). Depicting the ESP by contour lines on a slice through the molecule reveals its internal structure, but this is probably not as relevant to reactivity as the picture seen by mapping it onto the van der Waals surface, which is the picture presented to the outside molecular world. Examining the ESP interactions between a molecule and the active site of an enzyme can be important in drug design [82]. Various applications of the ESP are discussed by Politzer and Murray [192] and Brinck [169a].

Molecular orbitals

Visualization of molecular orbitals shows the location of those regions where the highest-energy electrons are concentrated (the highest occupied MO, the HOMO), and those regions which offer the lowest-energy accommodation to any donated electrons (the lowest unoccupied MO, the LUMO). Electrophiles should bond to the atom where the HOMO is “strongest” (where the electron density due to the highest-energy electron pair is greatest) and nucleophiles to the atom where the LUMO is strongest, at least as seen on the van der Waals surface by an approaching reagent. The information provided by inspection of the HOMO and LUMO (the frontier orbitals) is thus somewhat akin to that given by visualizing the ESP (electrophiles should tend to go to regions of

Ab initio calculations 321

negative ESP, nucleophiles to regions of positive ESP). Figure 5.49 shows the LUMOs of the ketones norcamphor and camphor, mapped onto their van der Waals surfaces. For norcamphor (Fig. 5.49(a)), the prominence of its LUMO at the carbonyl carbon as seen from the “top” or exo face (the face with the bridge) rather than the bottom (endo) face, suggests that nucleophiles should attack from the exo direction. In accord with this, hydride donors, for example, approach from the exo face to give mainly the

from this direction, and so nucleophiles tend to approach rather the endo face, a fact nicely rationalized by visualizing simultaneously the LUMO and the van der Waals surface (Fig. 5.49(b)) [193].

Figure 5.50 shows the LUMOs of three bicyclo[2.2.1]heptane derivatives (camphor and norcamphor, above, also have this carbon skeleton). The LUMOs are shown here as 3D regions of space, rather than mapping them onto a surface as was done in Fig. 5.49. Comparing the “composite” molecule (Fig. 5.50(c)) with the cation and the alkene clearly shows electronic interaction between the p orbital of the cationic carbon and the antibonding MO of the double bond.

Visualization–closing remarks

Other molecular properties and phenomena that can benefit from the aid of visualization are the distribution of unpaired electron spin in radicals and the changes in orbitals and charge distribution as a reaction progresses. These and many other visualization exercises are described in publications (e.g. [53c]) by Wavefunction, Inc. and in their visualization CD [194].