Ab initio calculations 289

How can this be reconciled with the results shown in this chapter and the modest levels endorsed by Hehre [32]? As hinted (“Don’t Panic!”; [1e], p. 146)], the large errors reported are a composite including some “tough cases” [150] like atomization energies (section 5.4.1). If the calculation set had been limited to, say, comparing the energies of isomers containing only carbon, hydrogen and oxygen, the errors would have been much smaller. A good feel for the accuracy of various levels of calculation will emerge from examining the extensive data in Hehre’s book [32], while Foresman and Frisch remind us that there are cases in which high-accuracy methods are required.

5.5.3 Frequencies

The calculation of normal-mode frequencies (section 2.5) is important because:

1.The number of imaginary frequencies tells us the curvature of the potential energy surface at the point corresponding to a particular stationary point: whether an optimized structure (i.e. a stationary point) is a minimum, a transition state (a first-order saddle point), or a higher-order saddle point. See section 2.5. Routinely checking optimized structures with a frequency calculation is a good idea, if the size of the job does not make this impractical (frequencies take longer than optimizations).

2.The frequencies must be calculated to get the zero point energy of the molecule. This is needed for accurate energy comparisons (section 2.5).

3.The normal-mode vibrational frequencies of a molecule correspond (with qualifications) to the bands seen in the infrared (IR) spectrum of the substance. Thus the IR spectrum of a substance that has never been made can be calculated to serve as a guide for the experimentalist. Unidentified IR bands observed in an experiment can sometimes be assigned to a particular substance on the basis of the calculated spectrum of a suspect; if the spectra of the usual suspects are not available from experiment (they might be extremely reactive, transient species), we can calculate them.

The characterization of stationary points by the number of imaginary frequencies was discussed in chapter 2, and ZPEs in chapter 2 and earlier sections of this chapter. Here we will examine the utility of ab initio calculations for the prediction of IR spectra [152]. It is important to remember that frequencies should be calculated at the same level (e.g. HF/3-21G, MP2/6-31G*,…) as was used for the geometry optimization (section 2.5).

Positions (frequencies) of IR bands

In section 2.5, we saw that diagonalization of the force constant matrix gives an eigenvalue matrix whose elements are the force constants of the normal modes, and an eigenvector matrix whose elements are their “direction vectors”. Mass-weighting the force constants gives the wavenumbers (“frequencies”) of the normal-mode vibrations, and their motions can be identified by using the direction vectors to animate them. So

290 Computational Chemistry

we can calculate the wavenumbers of IR bands and associate each band with some particular vibrational mode. The wavenumbers from ab initio calculations are larger than the experimental ones, i.e. the “frequencies” are too high. There are two reasons why this might be so: the principle of equating second derivatives of energy (with respect to geometry changes) with force constants might be at fault, or the basis set and/or correlation level might be deficient.

The principle of equating a second derivative with a stretching or bending force constant is not exactly correct. A second derivative 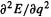is strictly equal to a force constant only for cases where the energy is a quadratic function of the geometry (simple harmonic motion), i.e. where a graph of E vs. q is a parabola, but vibrational curves are not parabolas (Fig. 5.32). For a parabolic E/q relationship, and considering a diatomic molecule for simplicity:

notjust one constant. Equation (5.198) holds for what is called simple harmonic motion, and the coefficients of the higher-power terms in the more accurate equation are called anharmonicity corrections. Assuming that bond vibrations are simple harmonic is the harmonic approximation.

For small molecules it is possible to calculate from the experimental IR spectrum the simple harmonic force constant k and the anharmonicity corrections. Using k, harmonic

Ab initio calculations 291

frequencies can be calculated [153], These correspond to a parabolic E/q relationship (Fig. 5.32), i.e. to a steeper curve than the real one, and thus to stiffer bonds. Stiffer bonds need more energy to stretch them (or bend them, for bending force constants), and thus absorb higher-frequency infrared light. Harmonic frequencies derived from experimental IR spectra are higher than the observed (the “raw”) experimental frequencies, and are closer to ab initio frequencies than are the observed frequencies [154]. Since both theoretically calculated (e.g. by ab initio methods) frequencies and experimentally-derived harmonic frequencies are based on a parabolic E/q relationship, it is sometimes considered better to compare calculated frequencies with harmonic frequencies rather than observed experimental frequencies [155].

Because both ab initio and experimentally-derived harmonic frequencies rest on second derivatives, we might expect ab initio frequencies to converge not toward the observed experimental, but rather toward the experimentally-derived harmonic frequencies, as correlation level/basis set are increased. This is indeed the case, as has been shown by calculations on water with high correlation levels (CCSD(T); section 5.4.3) and large basis sets (polarization functions and triplyor quadruply-split valence shells (section 5.3.3). The deviations fell from 269, 282, and 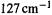at the Hartree-Fock level to values only 9, 13, and higher than the experimentally-derived harmonic values of 3943, 3832, and [156]. The observed water frequencies are 3756, 3657 and ; experimentally-derived harmonic frequencies are typically about 5% higher, and ab initio frequencies about 5–10% higher, than observed frequencies.

From the foregoing discussion it appears that ab initio frequencies are too high because of the harmonic approximation: equating of with a force constant. There is no theoretical reason why high-level calculations should converge toward the observed frequencies; this statement applies to frequencies calculated, as is almost always the case, by the harmonic approximation (above). However, we wish, ideally, to compute observed IR spectra. Fortunately, calculated and observed frequencies differ by a fairly constant factor, and ab initio frequencies can be brought into reasonable agreement with experiment by multiplying them by a correction factor. An extensive comparison by Scott and Radom of calculated and experimental frequencies [60] has provided empirical correction factors for frequencies calculated by a variety of methods. A few of the correction factors from this compilation are:

The correction factors at the HF level with the three basis sets are very similar, 0.90– 0.91; the factors at the MP2 level are significantly closer to 1, but Scott and Radom say that “MP2/6-31(d) does not appear to offer a significant improvement in performance over HF/6-31G(d) and occasionally shows large errors”, and “The most cost-effective procedures found in this study for predicting vibrational frequencies are HF/6-31(d) and [certain density functional methods]”. Scott and Radom have also derived separate correction factors for zero-point vibrational energies, although it was at least hitherto

292 Computational Chemistry

common practice to use the same correction factor for frequencies and for ZPE’s. Better agreement with experiment can be obtained by using empirical correction factors for specific kinds of vibrations (Scott and Radom give separate factors for low-frequency vibrations, as opposed to the relatively high-frequency ones to which the factors above refer), but this is rarely done.

Intensities of lR bands

The bands in an IR spectrum have not just positions (“frequencies”, denoted by various wavenumbers), but also intensities (not routinely quantified, but commonly described as weak, medium, or strong). To calculate an IR spectrum for comparison with experiment it is desirable to compute both wavenumbers and intensities. The intensity of an IR vibration is determined by the change in dipole moment accompanying the vibration. If a vibrational mode leads to no change in dipole moment, the mode will, theoretically, not result in absorption of an IR photon, because the oscillating electric fields of the radiation and the vibrational mode will be unable to couple. Such a vibrational mode is said to be IR-inactive, i.e. it should cause no observable band in the IR spectrum. Stretching vibrations that, because of symmetry, are not accompanied by a change in dipole moment, are expected to be IR-inactive. These occur mainly in homonuclear molecules like and and in linear molecules; thus the C/C triple bond stretch in symmetrical akynes, and the symmetric OCO stretch in carbon dioxide, do not engender bands in the IR spectrum. For Raman spectroscopy (in which one measures the scattered rather than the transmitted IR light), the requirement for observing a vibrational mode (i.e. for absorption of a photon) is that the vibration occur with a change in polarizability. Raman spectra are routinely calculable (e.g. by the Gaussian programs [23,48]; the IR and Raman frequencies are the same) along with IR spectra. A band which should be IR-inactive or at least very weak can in fact sometimes be seen because of coupling with other vibrational modes; thus the triple-bond stretch of benzyne dehydrobenzene) has been observed [157], although it apparently should be accompanied by only a very small change in dipole moment. Bands like this are expected to be, at best, weak.

As might be expected from the foregoing discussion, the intensity of an IR normal mode can be calculated from the change in dipole moment with respect to the change in geometry accompanying the vibration. The intensity is proportional to the square of the change in dipole moment with respect to geometry:

This can be used to calculate the relative intensities of IR bands (the calculation of dipole moments is discussed in the next section). One way to calculate the derivative is to approximate it as a ratio of finite increments d becomes ) and calculate the change in dipole moment with a small change in geometry; there are also analytical methods for calculating the derivative [158].

It has been reported that at the HF level calculated IR-band intensities often differ from experiment by a factor of over 100 percent, but at the MP2 level are typically within 30 percent ofexperiment [159]. A few calculated (frequencies and intensities) IR

Ab initio calculations 293

294 Computational Chemistry

296 Computational Chemistry

5.5.4 Properties arising from electron distribution: dipole moments, charges, bond orders, electrostatic potentials, atoms-in-molecules

We have seen three applications of ab initio calculations: finding the shapes (geometries), the relative energies, and the frequencies of stationary points (usually minima and transition states) on a potential energy surface. The shape of a molecular species is one of its fundamental characteristics. It can, for example, provide clues to the existence of theoretical principles (why is it that benzene has six equal-length CC bonds, but cyclobutadiene has two “short” and two “long” bonds [160]?), or act as a guide to designing useful molecules (docking a candidate drug into the active site of an enzyme