346 Computational Chemistry

same atom A are given the same value, 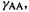and all two-center integrals between atoms A and B are given the same value, These integrals are calculated from valence s Slater functions on A and B.

CNDO/2 differs from CNDO/1 in two modifications to the matrix elements (Eq. (7.0)): (1) to account better for both ionization energy and electron affinity, is evaluated not just from ionization energy but as a kind of average of ionization energy and electron affinity, and (2) the integrals in the term are calculated from the two-electron integrals as 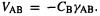This latter evaluation amounts to neglecting so-called penetration integrals; these integrals make nonbonded atoms attract one another, and causes bond lengths to be too short and bond energies to be too large [14–17]. CNDO energies are valence electron electronic energies E SE, or

electronic energies plus core–core repulsions, if is added (Eq. (6.2)). CNDO is not much used nowadays, having evolved into the less approximate semiempirical methods INDO and NDDO (below).

6.2.4The intermediate neglect of differential overlap (INDO) method

INDO [18] goes beyond CNDO by curtailing the application ofthe ZDO approximation. Instead of applying it to all different atomic orbitals in the two-electron integrals (Eq. (6.6)), as in the PPP and CNDO methods, in INDO ZDO is not applied to those one-center two-electron integrals, with and all on the same atom; obviously, these repulsion integrals should be the most important. Although more accurate than CNDO, INDO is nowadays used mostly only for calculating UV spectra, in specially parameterized versions called INDO/S and ZINDO/S [19].

6.2.5The neglect of diatomic differential overlap (NDDO) method

NDDO [20] goes beyond INDO in that the ZDO approximation (section 6.2.1, point (3)) is not applied to orbitals on the same atom, i.e. ZDO is used only for atomic orbitals on different atoms. NDDO is the basis of the currently popular semiempirical methods developed by Dewar and coworkers: modified NDDO (MNDO), Austin method 1 (AM1) and parametric method (PM3).

6.2.5.1NDDO-based methods from the Dewar group: MNDO, AM1, PM3 and SAM1 – preliminaries

SCF-type (see section 6.1) SE theories are based to a large extent on the approximate MO theory (see the book of this title [10]) developed by Pople and coworkers. The Pople school, however, went on to concentrate on the development of ab initio methods, and indeed it is for his contributions to these, which are largely encapsulated in the Gaussian series of programs [21], that Pople was awarded the 1998 Nobel Prize in chemistry [22] (shared with Walter Kohn, a pioneer in density functional theory; see

Semiempirical Calculations 347

chapter 7). In contrast, Dewar pursued the SE approach almost exclusively [23], and continued till the end of his career to stoutly maintain that at least as far as molecules of real chemical interest go his SE methods were superior to ab initio ones. (“There is clearly little point in using a procedure that requires thousands of times more computing time than ours do if it is no better than ours, let alone one that is inferior.”) [24]. The rivalry between the Dewar school and the adherents of the ab initio approach began relatively early in the development of Dewar methods (see, e.g. [25–27]), intensified to actual polemic [28], and is passionately described from an unabashedly partisan viewpoint in Dewar’s autobiography [23]. The ab initio vs. Dewar SE controversy was largely rooted in a difference of viewpoints and in a focus by Dewar on the inability of ab initio calculations to give reasonably accurate absolute molecular energies (an absolute molecular energy is the energy needed to dissociate a molecule into its nuclei and electrons, infinitely separated and at rest). In the absence of error cancellation, errors in absolute energies lead to errors in activation and reaction energies, and the errors in absolute energies were, ca. 1970, commonly in the region of a thousand kilojoules per mole. Cancellation (actually not as untrustworthy as Dewar thought – section 5.5.2.1) could not, he held, be relied on to provide chemically useful relative energies (reaction and activation energies), say up to some tens of kilojoules per mole. The exchange with Halgren, Kleir and Lipscomb nicely illustrates the viewpoint difference [27]: one side held that even when inaccurate, ab initio calculations can teach us something fundamental, while SE calculations, no matter how good, do not contribute to fundamental theory. Dewar focussed on the study of reactions of “real” chemical interest. Interestingly, the high-accuracy “ab initio” methods that in recent years have achieved chemical accuracy (section 5.5.2.2b), now considered to be about employ some empirical parameters, a fact that would have amused Dewar (section 6.1, footnote 1).

In contrast to the viewpoint of the ab initio school, Dewar regarded the SE method not merely as an approximation to ab initio calculations, but rather as an approach that, carefully parameterized, could give results far superior to those from ab initio calculations, at least for the foreseeable future: “The situation [ca. 1992] could be changed only by a huge increase in the speed of computers, larger than anything likely to be attained before the end of the century, or by the development of some fundamentally better ab initio approach.” [29]. The conscious decision to achieve experimental accuracy rather than merely to approximate ab initio results (note the remarks in connection with Eq. (6.12)) was clearly stated several times [26,28,30] in the course of the development of these SE methods: “We set out to parametrize [semiempirical methods] in an entirely different manner, to reproduce the results of experiment rather than those of dubious ab initio calculations.” [30].

The first (1967) of the Dewar-type methods was PNDDO [31] (partial NDDO). Because further development of the NDDO approach turned out to be “unexpectedly formidable” [30], Dewar’s group temporarily turned to INDO, creating MINDO/1 [32] (modified INDO, version 1). The third version of this method, MINDO/3, was said [30] “[to have] so far survived every test without serious failure,” and it became the first widely-used Dewar-type method, but keeping their promise to return to NDDO the group soon came up with MNDO. MINDO/3 was made essentially obsolete by MNDO, except perhaps for the study of carbocations (Clark has summarized the strengths and

348 Computational Chemistry

weaknesses of MINDO/3, and the early work on MNDO [33]). MNDO and its descendants AM1 and PM3 are discussed below. A modification of AM1, SAM1, is briefly mentioned; it has not (yet?) gained much popularity.

6.2.5.2 Heats of formation from SE electronic energies

Of the several experimental parameters that the Dewar methods are designed to reproduce, probably the two most important are geometry and heat of formation. For heat of formation the procedure encoded in the methods is the following [34]. As with ab initio calculations, SCF-type SE calculations initially give electronic energies these are calculated using Eq. (6.2). Inclusion of the core–core repulsion which is necessary for geometry optimization, gives the total semiempirical energy normally expressed in atomic units (hartrees), as in an ab initio calculation (e.g. section 5.2.3.6e). This energy the total internal energy of the molecule except for zero point vibrational energy, is used to calculate the heat of formation (enthalpy of formation) of the molecule. Figure 6.1 will help to make it clear how this is done. The quantities in

Fig. 6.1 are

(1) 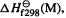the experimental 298 K heat of formation of the molecule M, i.e. the heat energy needed to make M from its elements. This is the quantity we want.

(2)The atomization energy ofM, which is the energy of the atoms minus the energy of M. The energy of the atoms is the conversion factor F converts

optimized geometry being used. The same SE method is used to calculate atomic and molecular energies, both of which are negative quantities, the energy of the species relative to electrons and one or more atomic cores infinitely separated. is

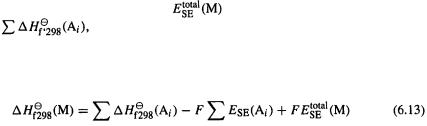
Semiempirical Calculations 349

purely electronic, since an atom has no core–core repulsion (i.e. it has no atoms to

heats of formation of these atoms.

Equating the two paths from the elements in their standard states at 298 K to atoms we get

Thus the desired quantity, the heat of formation of the molecule, can be calculated from the experimental heats of formation of the atoms and the semiempirical energies of the atoms and the molecule. The calculation of Eq. (6.13) is automatically done by the program using stored values for atomic heats of formation and semiempirical atomic energies, and the “freshly calculated” calculated molecular energy, and one normally never sees These calculations are for the gas phase, and if one wants the heat of formation of a liquid or a solid, then the experimental heat of vaporization or sublimation must be taken into account. Note that this procedure is conceptually almost the same as the atomization method for ab initio calculation of heats of formation (section 5.5.2.2c). However, the purpose here is to obtain the heat of formation at room temperature (298 K) from the molecular “total semiempirical energy,” the electronic energy plus core–core repulsion; in the ab initio atomization method the 0 K heat of formation is calculated with the aid of the molecular energy including ZPE (the 0 K heat of formation can be corrected to 298 K – see section 5.5.2.2c). The SE procedure involves some approximations. The ZPE of the molecule is not used, and the increase in thermal energy from 0 to 298 K is not calculated. Thus if were fully analogous to the ab initio 0 K electronic energy plus internuclear repulsion then the calculated atomization energy would be at 0 K, not 298 K, and furthermore would employ a frozen-nucleus approximation to the true 0 K energy. The good news is that is parameterized (below) to reproduce 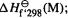to the extent that this parameterization succeeds the neglect of ZPE and of the 0–298 K increase in thermal energy are overcome (and electron correlation is also implicitly taken into account). The key to obtaining reasonably accurate heats of formation from these methods is thus their parameterization to give the values of and used in Eq. (6.13). This parameterization, which is designed to also give reasonable geometries and dipole moments, is discussed below.

6.2.5.3 MNDO

MNDO [33], a modified NDDO (section 6.2.5) method, was reported in 1977 [35]. MNDO is conveniently explained by reference to CNDO (section 6.2.3). MNDO is a general geometry method with a minimal valence basis set of Slater-type orbitals, the one-center core integrals. The Fock matrix elements are calculated using Eq. (6.1). We discuss the core and two-electron integrals in the same order as for CNDO.

The core integrals with the same orbital twice on the same atom A are calculated using Eq. (6.10). Unlike the case in CNDO, where 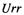is found from ionization energies (CNDO/1) or ionization energies and electron affinities (CNDO/2), in

350 Computational Chemistry

MNDO is one of the parameters to be adjusted. The integrals in the summation term 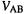are evaluated similarly to the CNDO/2 method from a two-electron integral (see below)involving and the valence s orbital on atom B:

The core integrals with different orbitals and , on the same atom A are not simply taken as being proportional to the overlap integral, as in CNDO (Eq. (6.12)), but rather are also (like the case of both orbitals on the same atom) evaluated from Eq. (6.10), which in this case becomes

The first term is zero from symmetry [36]. Each integral of the summation term is again evaluated, as in CNDO/2, from a two-electron integral:

The core integrals with different orbitals and on different atoms A and B are taken, as in CNDO (cf. Eq. (6.12)), to be proportional to the overlap integral between and where again the proportionality constant is the arithmetic mean of parameters for atoms A and B:

The overlap integral is calculated from the basis functions although the overlap matrix is taken as a unit matrix as far as the Roothaan–Hall equations go (section 6.2.2). These core integrals are sometimes called core resonance integrals.

The two-electron integrals are evaluated applying ZDO (section 6.2.1) within the framework of the NDDO approximation (section 6.2.5). As with the PPP (section 6.2.2) and CNDO (section 6.2.3) methods, this makes all two-electron integrals become , i.e only oneand two-center two-electron integrals are nonzero. The one-center integrals are evaluated from valence-state ionization energies. The two-center integrals are evaluated from the one-center integrals and the separation of the nuclei by an involved procedure in which the integrals are expanded as sums of multipole-multipole interactions [35a,37] that make the two-center integrals show correct limiting behavior at zero and infinite separation.

As in CNDO the penetration integrals are neglected (section 6.2.3, CNDO/2). A consequence of this is that the core–core repulsions in Eq. (6.2)) cannot be realistically calculated simply as the sum of pairs of classical electrostatic interactions between point charges centered on the nuclei. Instead, Dewar and coworkers chose [35a] the expression

Semiempirical Calculations 351

where and are the core charges of atoms A and B and and are the valence s orbitals on A and B (the two-electron integral in Eq. (6.18) is actually approximately proportional to so there is some connection with the simple electrostatic model). The term is a correction increment to make the result come out better; it depends on the core charges and the valence s functions on A and B, their separation R, and empirical parameters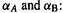

The above mathematical treatment constitutes the creation of the form of the semiempirical equations; to actually use these equations, they must be parameterized using experimental data. This is analogous to the situation in molecular mechanics (chapter 3), where a force field, defined by the form of the functions used (e.g. a quadratic function of the amount by which a bond is stretched, for the bond-stretch energy term) is constructed, and must then be parameterized by inserting specific quantities for the parameters (e.g. values for the stretching force constants of various bonds). For each kind of atom A (a maximum of) six parameters is needed:

(1)The kinetic-energy-containing term of Eq. (6.10) (as explained above, this CNDO equation is also used in MNDO to evaluate where is a valence s AO.

(2)The term 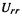of Eq (6.10) where is a valence p AO.

(3)The parameter in the exponent of the Slater function (e.g. section 5.3.2, Fig. 5.12) for the various valence AOs (MNDO uses the same for the s and p AOs).

(4)The parameter (Eq. (6.17)) for a valence s AO.

(5)The parameter for a valence p AO.

(6)the parameter in the correction increment (Eq. (6.19)) to the core–core repulsion (Eq. (6.18)).

Some atoms have five parameters because for them MNDO takes to be the same for s and p orbitals, and hydrogen has four parameters because MNDO does not assign it p orbitals.

We want the parameters that will give the best results, for a wide range of molecules. What we mean by “results” depends on the molecular characteristics of most interest to us. MNDO (and its siblings AM1 and PM3, below) was parameterized [35a] to reproduce heat of formation, geometry, dipole moment, and the first vertical ionization energy (from Koopmans’ theorem; section 5.5.5). To parameterize MNDO a training set of molecules (a “molecular basis set” is Dewar’s term – no connection with a basis set of functions used to construct MOs) of small, common molecules (e.g. methane, benzene, dinitrogen, water, methanol; 34 molecules were used for the C, H, O, N set) was chosen and the six parameters above were adjusted in an attempt to give the best values of the four molecular characteristics (heat of formation, geometry, dipole moment, and ionization energy). Specifically, the objective was to minimize Y, the sum of the weighted squares of the deviations from experiment of the

352 Computational Chemistry

four molecular characteristics:

of assigning values to the parameters is formally analogous to the problem of geometry optimization (section 2.4). In geometry optimization we want the set of atomic coordinates that correspond to a minimum (sometimes to a transition state) on a potential energy hypersurface. In parameterizing a SE method we want the set of parameters that correspond to the minimum overall calculated deviation of the chosen characteristics from their experimental values – the parameters that give the minimum Y, above. Details of the parameterization process for MNDO have been given by Dewar [35a] and by Stewart [38].

The results of MNDO calculations on 138 compounds limited to the elements C, H, O, N were reported by Dewar and Thiel [35b]. The absolute mean errors were:

in dipole moment, 0.30 D for 57 compounds; in ionization energy, 0.48 eV for 51

MNDO can reproduce these and other properties of a wide variety of molecules [33,39], it is little used nowadays, having been largely superseded by AM1 and, to a somewhat lesser extent, PM3 (below). More results from MNDO calculations are given in section 6.3.

6.2.5.4 AM1

Austin method 1 (AM1, developed at the University of Texas at Austin [40]) was introduced by Dewar, Zoebisch, Healy, and Stewart in 1985 [41]. AM1 is an improved version of MNDO in which the main change is that the core–core repulsions (Eq. (6.18)) were modified to overcome the tendency of MNDO to overestimate repulsions between atoms separated by about their van der Waals distances (the other change is that the parameter in the exponent of the Slater function – see parameter 3 in the listing of the six parameters above – need not be the same for s and p AOs on the same atom). The core–core repulsions were modified by introducing attractive and repulsive Gaussian functions centered at internuclear points [42], and the method was then reparameterized. The great difficulties experienced in the parameterization of AM1 and its predecessors are emphasized by Dewar and coworkers in many places, e.g.: “All our work has therefore been based on a very laborious purely empirical technique...” for the MINDO methods [30]; parameterization is a “purely empirical affair” and “needs infinite patience and enormous amounts of computer time,” for AM 1 [41 ]. In his autobiography Dewar says [43] “This success [of these methods] is no accident and it has not been obtained easily,” and summarizes the problems with parameterizing these

Semiempirical Calculations 353

methods: (1) the parametric functions are of unknown form, (2) the choice of molecules for the training set affects the parameters to some extent, (3) the parameters are not unique, there is no way to tell if the set of values found is the best one, and there is no systematic way to find alternative sets, (4) deciding if a set of parameters is acceptable is a matter of judgment. Dewar et al. chose to call their modified MNDO method AM1, rather than MNDO/2, because they felt that their methods were being confused (presumably because of the “INDO” and “NDO” components of the appellations) with “grossly inaccurate” [41] ZDO SCF SE methods like CNDO and INDO.

Dewar, Zoebisch, Healy, and Stewart reported [41] that AM1 calculations on compounds containing nitrogen and/or oxygen gave an absolute mean error in heat of formation of for 80 compounds, “generally satisfactory” agreement with experiment for the geometries of 138 molecules, absolute mean error in dipole moment of 0.26 D for 46 compounds, and absolute mean error in ionization energy of 0.40 eV for 29 compounds. These results are slightly better than those for MNDO, but the real advantages of AM 1 over MNDO were said [41 ] to lie in its better treatment of hydrogen bonding, crowded molecules, four-membered rings, and activation energies. AM1 is the most widely-used SE method nowadays. MNDO and AM1 (and PM3, below) are compared further in section 6.3.

6.2.5.5 PM3

PM3 is a variation of AM1, differing mainly in how the parameterization is done. When PM3 was first published [38], two parameterizations of MNDO-type methods, MNDO and AM1, had been carried out, and PM3 was at first called MNDO-PM3, meaning MNDO parametric method 3. Three papers [38,44,45] define the PM3 method. The Dewar school’s approach to parameterization was a painstaking one (section 6.2.5.4), making liberal use of chemical intuition. The developer of PM3, Stewart, employed a faster, more algorithmic approach, “several orders of magnitude faster than those previously employed” [38]. Although it is based on AM1, PM3 did not enjoy Dewar’s blessing. The reasons for this appear to be at least twofold: (1) Dewar evidently felt (on the basis of very early results [46]) that PM3 represented at best an only marginal improvement over AM1, and that a new SE method should make previous ones essentially obsolete, as MNDO made MINDO/3 obsolete, and AM1 largely replaced MNDO. Stewart defended his approach [47] with the rejoinder, inter alia, that if PM3 was only a only marginal improvement over AM1, then AM1 was only a marginal improvement over MNDO. (2) Dewar objected strongly to any proliferation of computational chemistry methods, whether it be in the realm of ab initio basis sets [48] or of SE methods [46,48].

For compounds containing H, C, N, O, F, Cl, Br, and I, Holder et al. reported [49] that

for AM1) [50], and 0.40 D for 196 compounds (cf. 0.35 D for AM1) [50]. PM3 is the second most widely-used semiempirical method nowadays (after AM1). MNDO, AM1, and PM3 are compared further in section 6.3.