Semiempirical Calculations 373

are not greatly altered. For the protonated enone system, AM1 and PM3 suggest more polarization of electrons toward the O in the C/O bond than is shown by the Mulliken charges, but while the HF ESP charge on this carbon is greater than the Mulliken (0.76 vs. 0.45), the charge on oxygen is unchanged. The HF Löwdin bond orders for all three bonds of the CCCO framework (1.55, 1.29, 1.76) are all somewhat bigger than the Mulliken bond orders (1.18,1.15, 1.59).

These results indicate that charges are more dependent than are bond orders on the method used to calculate them, and that charges are also harder to interpret than are bond orders. As with ab initio charges and bond orders, the semiempirically calculated parameters may be useful in revealing trends in a series of compounds or changes as a reaction proceeds. For example, ab initio bond order changes along a reaction coordinate have been shown to be useful [77], but presumably semiempirically calculated bond orders would also yield similar information, at least if the species being studied were not too exotic. Clearly, one must use the same semiempirical method (e.g. AM1) and the same procedure (e.g. the Mulliken procedure) in studying a series of species.

6.3.5Miscellaneous properties – UV spectra, ionization energies, and electron affinities

All the properties that can be calculated by ab initio methods can in principle also be calculated semiempirically, bearing in mind that the more the molecule of interest differs from the training set used to parameterize the SE program, the less reliable the results will be. For example, a program parameterized to predict the UV spectra of aromatic hydrocarbons may not give good predictions for the UV spectra of heterocyclic compounds. NMR spectra are usually calculated with ab initio (section 5.5.5) or density functional (chapter 7) methods. UV spectra, and ionization energies (ionization potentials) and electron affinities will be discussed here.

UV spectra

As pointed out in section 5.5.5, although ultraviolet spectra result from the promotion of electrons from occupied to unoccupied orbitals, UV spectra cannot be calculated with reasonable accuracy simply from the HOMO/LUMO gap of the ground electronic state, since the UV bands represent energy differences between the ground and excited states. Furthermore the HOMO/LUMO gap does not account for the presence of the several bands often found in UV spectra, and gives no indication of the intensity of a band. Accurate prediction of UV spectra requires calculation of the energies of excited states. SE UV spectra are usually calculated with programs specifically parameterized for this purpose, such as INDO/S or ZINDO/S (section 6.2.4) [19], both of which are in, e.g. HyperChem [78]. ZINDO/S, which appears to have largely superseded INDO/S, is included in the primarily ab initio and DFT package Gaussian 98 [79]. Table 6.6 compares the UV spectrum of methylenecyclopropene calculated by ZINDO/S as implemented in Gaussian 98 for Windows (G98W) [80] with the ab initio-calculated (Table 5.20; the geometry for this was calculated by DFT – chapter 7) and the experimental spectra [81]. The ZINDO/S spectrum resembles the experimental spectrum

374 Computational Chemistry

considerably better than does the ab initio one (the experimental 242 nm, and particularly the 309-nm band, are matched better than by the ab initio calculation). The times for the calculations, on a 200 MHZ PentiumPro running Windows NT, were 53 s (ZINDO) and 11 min (ab initio).

lonization energies and electron affinities

The concepts of IE and EA were discussed in section 5.5.5. In Table 6.7, the results of some semiempirical calculations are compared with ab initio and experimental values, for the molecules of Table 5.21. This admittedly very small sample suggests that SE IEs calculated as energy differences might be comparable to ab initio values. Koopmans’ theorem (the IE for an electron is approximately the negative of the energy of its molecular orbital; applying this to the HOMO gives the IE of the molecule) values are consistently bigger than those from energy differences using the same method (by 0.1–0.8 eV). No consistent advantage for any of the six methods is evident here, but a large sample would likely show the most accurate of these methods to be the energy difference using MP2(fc)/6-31G* (see Table 5.21 and accompanying discussion).

Calculations by Stewart on 256 molecules (of which 201 were organic), using Koopmans’ theorem, gave mean absolute IE errors of 0.61 eV for AM1 and 0.57 eV

Semiempirical Calculations 375

for PM3; 60 of the AM1 errors (23%) and 88 of the PM3 (34%) were negative (smaller than the experimental values) [44]. Particularly large errors (2.0–2.9 eV) were reported for nine molecules: 1-pentene, 2-methyl-1-butene, acetylacetone, alanine (AM1), (AM1),CF 3Cl(AM1),1,2-dibromotetrafluoroethane, (PM3), and 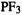(AM1). For some these it may be the experimental results that are at fault; for example, there seems to be no reason why 2-methyl-1-butene and 2-methyl-2-butene should have such different IEs, and in the opposite order to those calculated: experimental, 7.4 and 8.7 eV; calculated, 9.7 and 9.3 (AM1), 9.85 and 9.4 eV (PM3), respectively. Ab initio (HF/3-21G) energy-difference calculations by the author give IEs in line with the AM1, rather than the claimed experimental, results: 2-methyl-1-butene, 9.4 eV; 2-methyl-2- butene, 9.1 eV. Calculations by the author on the first 50 of these 256 molecules (of these 50 all but and 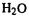are organic) gave these mean absolute IE errors: AM1, 0.46 (12 negative); PM3, 0.58 (5 negative); ab initio HF/3-21G, 0.71 (11 negative). So for the set of 256 mostly organic molecules AM1 and PM3 gave essentially the same accuracy, and for the set of 50 molecules AM1 was slightly better than PM3 and the ab initio method was slightly worse than the semiempirical ones. The HF/3-21G level is the lowest ab initio one routinely used (or at least reported) nowadays; ionization energies and electron affinities comparable in accuracy to those from experiment can be obtained by high-accuracy ab initio calculations (sections 5.5.2.2b and 5.5.5), using the energy difference of the two species involved.

Dewar and Rzepa found that the MNDO (section 6.2.5.3) electron affinities of 26 molecules with delocalized HOMOs (mostly radicals and conjugated organic molecules) had an absolute mean error of 0.43 eV; for ten molecules with the HOMO localized on one atom, the error was 1.40eV [82]. The errors from AM1 or PM3 should be less than for these MNDO calculations.

6.3.6 Visualization

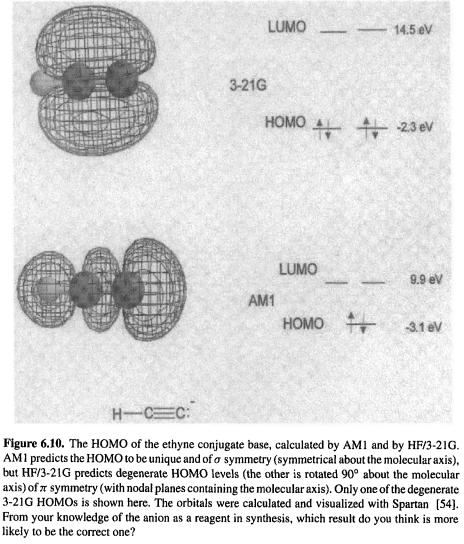
Many molecular features that have been calculated semiempirically can be visualized, in a manner analogous to the case of ab initio calculations (section 5.5.6). Clearly, one wishes to be able to view the molecule, rotate it, and query it for geometric parameters. Semiempirically calculated vibrations, electrostatic potentials, and molecular orbitals also provide useful information when visualized, and little need be added beyond that already discussed for the visualization of ab initio results. AM1 and PM3 surfaces (van der Waals surfaces, electrostatic potentials, orbitals) are usually very similar in appearance to those calculated by ab initio methods, but exceptions occasionally occur. An example is the case of HCC¯ , the conjugate base of ethyne (acetylene), Fig. 6.10. AM1 predicts that there is one HOMO and that it is of a symmetry (symmetric about the molecular axis), but a HF/3-21G calculation predicts that there are two HOMOs of equal energy at right angles, each of symmetry (having a nodal plane containing the molecular axis; one of these -HOMOs is shown in Fig. 6.10). The 3-21G orbital pattern persists at the HF/6-31G* and MP2/6-31G* levels. Different orbital patterns at different calculational levels is not the rule, but is understandable since energetically close MOs may have their energetic priorities reversed on going to a different level.

376 Computational Chemistry

6.3.7 Some general remarks

Parameterized methods like ZINDO/S are probably the only way to calculate reasonably accurate UV spectra for large molecules. AM1 and PM3 have become extremely useful not only because they allow quantum mechanical calculations to be done on molecules which are still too big for ab initio or DFT (chapter 7) methods, but also as adjuncts to these latter methods, since they often allow a relatively rapid survey of a problem, such as an exploration of a potential energy surface: one can locate minima and transition states, then use the semiempirical structures (size permitting) as inputs for initial geometries, wavefunctions and hessians (section 2.4) in a higher-level geometry