Semiempirical Calculations 377

optimization. If geometry optimizations are not feasible, single-point calculations on AM1 or PM3 geometries (which are usually reasonably good) will likely give improved relative energies. The time is well past when SE calculations were regarded by many as “worthless” [85], or, at best, as a poor substitute for ab initio calculations.

6.4 STRENGTHS AND WEAKNESSES OF SE METHODS

These remarks refer to AM1 and PM3 (and SAM1).

Strengths

Semiempirical calculations are very fast compared to ab initio and even to DFT (chapter 7), and this speed is often obtained with only an inconsequential loss of accuracy. Semiempirical geometries of normal molecules are entirely adequate for many purposes, and even transition state geometries are often adequate. Reaction and activation energies, although not accurate (except by chance cancellation of heat of formation errors), will probably expose any marked trends. Surprisingly, although they were parameterized using normal, stable molecules, AM1 and PM3 usually give fairly realistic geometries and relative energies for cations, radicals, anions, strained molecules, and even transition states.

Weaknesses

A major weakness of SE methods is that they must be assumed to be unreliable outside molecules of the kind used for their training set (the set of molecules used to parameterize them), until shown otherwise by comparison of their predictions with experiment or with high-level ab initio (or probably DFT) calculations. Although, as Dewar pointed out [86], the reliability of ab initio calculations, too, should be checked against experiment, the situation is somewhat different for these latter, at least at the higher levels; studies of exotic species, in particular, are certainly more trustworthy when done ab initio than semiempirically (see chapter 8). SE heats of formation are subject to errors

timate basicity and underestimate nucleophilicity, and can give unreasonable charges and structures; PM3 has been reported to tend to give more reliable structures, and AM1 better energies [76]. Neither AM1 nor PM3 are generally reliable in modelling hydrogen bonds [87,88], and SAM1 appears to be the Semiempirical method of choice here [51].

In general, the accuracy of SE methods, particularly in energetics, falls short of that of current routine ab initio methods (this may not have been the case when AM1 was developed, in 1985 [86]). Parameters may not be available for the elements in the molecules one is interested in, and obtaining new parameters is something rarely done by people not actively engaged in developing new methods. SE errors are less systematic than ab initio, and thus harder to correct for.

378 Computational Chemistry

6.5 SUMMARY OF CHAPTER 6

Semiempirical quantum mechanical calculations are based on the Schrödinger equation. This chapter deals with SCF SE methods, in which repeated diagonalization of the Fock matrix refines the wavefunction and the molecular energy (the SHM and EHM, in contrast, need only one matrix diagonalization because their matrix elements are not calculated using a wavefunction guess – see chapter 4). These calculations are much faster than ab initio ones, mainly because the number of integrals to be dealt with is greatly reduced by ignoring some, some integrals are approximated with the help of experimental quantities (hence “empirical”), and other integrals are calculated only approximately. In order of increasing sophistication, these SCF SE procedures have been developed: PPP, CNDO, INDO, and NDDO. The PPP method is limited to electrons, while CNDO, INDO and NDDO use all the valence electrons. All four use the ZDO approximation, which sets the differential of the overlap integral equal to zero; this greatly reduces the number of integrals to be calculated. Traditionally, these methods were parameterized mostly using experimental quantities (usually ionization energies and electron affinities), but also (PPP and CNDO) making some use ofminimal- basis-set (i.e. low-level) ab initio calculations. Of these original methods, only versions of INDO parameterized to reproduce UV spectra (INDO/S and its variant ZINDO/S) are much used nowadays. Today by far the most popular SCF SE methods are AM1 and PM3, which are NDDO-based, but carefully parameterized to reproduce experimental quantities (primarily heats of formation). AM1 and PM3 perform similarly and usually give quite good geometries, but less satisfactory heats of formation and relative energies. A modification of AM1 called SAM1, as yet relatively little-used, is said to be an improvement over AM1. AM1 and SAM1 represent work by the group of Dewar; PM3 is a version of AM1, by Stewart, differing mainly in a more automatic approach to parameterization.

REFERENCES

[1](a) S. Weinberg, “Dreams of a Final Theory: the Search for the Fundamental Laws of Nature,” Pantheon Books, New York, 1992. (b) Measuring the physical constants: A. Watson, Science, 2000, 287,1391.

[2]D. R. Hartree, Proc. Cambridge Phil. Soc., 1928, 24, 89, 111, 426.

[3]The history of the development of computational chemistry (in the United States): J. D. Bolcer and R. B. Hermann, in Reviews in Computational Chemistry, vol. 8, K. B. Lipkowitz and D. B. Boyd, Eds., VCH, New York, 1994, chapter 1.

[4]Ref. [3, p. 12].

[5]M. J. S. Dewar, “The Molecular Orbital Theory of Organic Chemistry,” McGraw-Hill, New York, 1969, p. 73.

[6]A single-point HF/6-31G* calculation on l,3,5-triamino-2,4,6-trinitrobenzene, 282 basis functions; this was said to require 2.6 h on a 90 MHz pentium machine: Gaussian News, Summer 1995. This calculation on the conformation, using a 650 MHz Pentium III, took 13 and 46 min with two popular programs (February 2000).

Semiempirical Calculations 379

[7]M. J. S. Dewar, “The Molecular Orbital Theory of Organic Chemistry,” McGraw-Hill, New York, 1969, chapter 3.

[8]I. N. Levine, “Quantum Chemistry,” 5th Ed., Prentice Hall, Upper Saddle River, New Jersey, 2000, chapter 16.

[9]W. Thiel in Advances in Chemical Physics, Volume XCIII, I. Prigogine and S. A. Rice, Eds., Wiley, New York, 1996.

[10]J. A. Pople and D. L. Beveridge, “Approximate Molecular Orbital Theory,” McGraw-Hill, New York, 1970.

[11]R. Pariser and R. G. Parr, J. Chem. Phys., 1953, 21, 466, 767.

[12]J. A. Pople, Trans. Faraday Soc., 1953, 49, 1475.

[13](a) Chemie in unserer Zeit, 1993, 12, 21–31; (b) J. Griffiths, Chemistry in Britain, 1986, 22, 997–1000.

[14]J. A. Pople and G A. Segal, J. Chem. Phys., 1966, 44, 3289, and references therein.

[15]P. Coffey, Int. J. Quantum Chem., 1974, 8, 263.

[16]Ref. [7, pp. 90–91].

[17]Ref. [10, p. 76].

[18](a) J. A. Pople, D. L. Beveridge, and P. A. Dobosh, J. Chem. Phys., 1967, 47, 2026;

(b)R. N. Dixon, Mol. Phys., 1967, 12, 83.

[19]INDO/S: M. Kotzian, N. Rösch, and M. C. Zerner, Theor. Chim. Acta, 1992, 81, 201.

(b)ZINDO/S is a version of INDO/S with some modifications, plus the ability to handle

transition metals. The Z comes from the name of the late Professor Michael C. Zerner, whose group developed the suite of (mostly SE) programs called ZINDO, which includes ZINDO/S. ZINDO is available from, e.g. Molecular Simulations Inc., San Diego, CA., and CAChe Scientific, Beaverton, OR.

[20]J. A. Pople, D. P. Santry, and G. A. Segal, J. Chem. Phys., 1965, 43, S129; J. A. Pople and G. A. Segal, J. Chem. Phys., 1965, 43, S136; J. A. Pople and G. A. Segal, J. Chem. Phys.,

1966, 44, 3289.

[21]D. B. Boyd in Reviews in Computational Chemistry, vol. 6, K. B. Lipkowitz and D. B. Boyd, Eds., VCH, New York, 1995, chapter 5.

[22](a) E. Wilson, Chemical & Engineering News, 1998, October 19, 12; (b) D. Malakoff, Science, 1998, 282, 610; (c) Nobel lecture: Angew. Chem. Int. Ed., 1999, 38, 1895.

[23]M. J. S. Dewar, “A Semiempirical Life,” American Chemical Society, Washington, DC, 1992.

[24]Ref. [23, p. 131].

[25]M. J. S. Dewar, J. Am. Chem. Soc., 1975, 97, 6591.

[26]M. J. S. Dewar, Science, 1975, 187, 1037.

[27]T. A. Halgren, D. A. Kleier, and W, N. Lipscomb, Science, 1975, 190, 591; response: M. J. S. Dewar, Science, 1975, 190, 591.

[28]M. J. S. Dewar, J. Mol. Struct., 1983, 100, 41.

[29]Ref. [23. p. 125].

[30]R. C. Bingham, M. J. S. Dewar, and D. H. Lo, J. Am. Chem. Soc., 1975, 97, 1285.

[31]M. J. S. Dewar and G. Klopman, J. Am. Chem. Soc., 1967, 89, 3089.

[32]N. C. Baird and M. J. S. Dewar, J. Chem. Phys., 1969, 50, 1262.

380Computational Chemistry

[33]T. Clark, “A Handbook of Computational Chemistry,” Wiley, New York, 1985, chapter 4.

[34]Ref. [8, p. 659].

[35](a) First appearance of MNDO: M. J. S. Dewar and W. Thiel, J. Am. Chem. Soc., 1977,99, 4899. (b) Results of MNDO calculations on molecules with H, C, N, O: M. J. S. Dewar and W. Thiel, J. Am. Chem. Soc., 1977, 99, 4907. (c) Results for molecules with B: M. J. S. Dewar and M. L. McKee, J. Am. Chem. Soc., 1977, 99, 5231.

[36]P. O’D. Offenhartz, “Atomic and Molecular Orbital theory,” McGraw-Hill, New York, 1970, p. 325 (these matix elements are zero because the AO functions belong to different symmetry species, while the operator (kinetic plus potential energy) is spherically symmetric).

[37]M. J. S. Dewar and W. Thiel, Theor. Chim. Acta, 1977, 46, 89.

[38]J. J. P. Stewart, J. Comp. Chem., 1989, 10, 209.

[39]W. Thiel, Tetrahedron, 1988, 44, 7393.

[40]For Dewar’s very personal reminiscences of Austin see Ref. [23, pp. 111–120].

[41]M. J. S. Dewar, E. G. Zoebisch, E. F. Healy, and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902.

[42]Note particularly Ref. [8, p. 662].

[43]Ref. [23, pp. 134, 135].

[44]J. J. P. Stewart, J. Comp. Chem., 1989, 10, 221.

[45]J. J. P. Stewart, J. Comp. Chem., 1991, 12, 320.

[46]M. J. S. Dewar, E. F. Healy, A. J. Holder, and Y.-C. Yuan, J. Comp. Chem., 1990, 11, 541.

[47]J. J. P. Stewart, J. Comp. Chem., 1990, 11, 543.

[48]Ref. [23, p. 185].

[49]A. J. Holder, R. D. Dennington, and C. Jie, Tetrahedron, 1994, 50, 627.

[50]M. J. S. Dewar, C. Jie, and J. Yu, Tetrahedron, 1993, 49, 5003.

[51]A. J. Holder and E. M. Evleth, in Chapter 7 in Modelling the Hydrogen Bond, D. A. Smith, Ed., American Chemical Society, Washington, DC, 1994.

[52]AMPAC 4.5 with Graphical User Interface: Semichem, P.O.Box 1649, Shawnee Misssion, KS 66216. www.Semichem.com.

[53]W. Thiel and A. A. Voityuk, J. Am. Chem. Soc., 1996, 100, 616.

[54]Spartan: Wavefunction, Inc., 18401 Von Karman, Suite 370, Irvine CA. www.wavefun.com.

[55]R. Bosque and F. Maseras, J. Comp. Chem., 2000, 21, 562.

[56]W. Thiel, J. Am. Chem. Soc., 1981, 103, 1413, 1421; A. Schweig and W. Thiel, J. Am. Chem. Soc., 1981, 103, 1425.

[57]Ref. [8, chapters 16 and 17] and references therein.

[58]W. J. Hehre, “Practical Strategies for Electronic Structure Calculations,” Wavefunction, Inc., Irvine, CA, 1995.

[59]J. J. P. Stewart, J. Mol. Struct. (Theochem), 1997, 410, 195.

[60]MOZYME is a program in the suite of SE programs called MOPAC 2000, developed by J. J. P. Stewart: MOPAC has MINDO/3, MNDO, AM 1 and PM3.

[61]J. J. P. Stewart, Int. J. Quantum Chem., 1996, 58, 133.

[62]S. Schröder and W. Thiel, J. Am. Chem. Soc., 1985, 107, 4422.

Semiempirical Calculations 381

[63]W. J. Hehre, L. Radom, P. V. R. Schleyer, and J. A. Pople, “Ab initio Molecular Orbital Theory,” Wiley, New York, 1986.

[64]W. Thiel, in “Computational Thermochemistry,” K. K. Irikura and D. J. Frurip, Eds., American Chemical Society, Washington, DC, 1998, chapter 8.

[65]J. B. Pedley, “Thermochemical Data and Structures of Organic Compounds,” Thermodynamics Research Center, College Station, Texas, 1994.

[66](a) 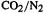copolymers: J. Bylykbashi and E. Lewars, J. Mol. Struct. (Theochem), 1999, 469, 77. (b) Oxirenes: E. Lewars, Can. J. Chem., 2000, 78, 297–306.

[67] reaction E. Lewars and I. Bonnycastle, J. Mol. Struct. (Theochem), 1997, 418, 17 and references therein. HNC reaction V. S. Rao, A. Vijay, A. K. Chandra, Can. J. Chem., 1996, 74, 1072. reaction The reported experimental activation energy is F. W. Schneider and B. S. Rabinovitch, J. Am. Chem. Soc., 1962, 84, 4215; B. S. Rabinovitch and P. W. Gilderson, J. Am. Chem. Soc., 1965, 87, 158. The energy of CH3CN relative to CH3NC by a high-level (G2) calculation is (E. Lewars). An early ab initio study of the reaction: D. H. Liskow, C. F. Bender, H. F. Schaefer, J. Am. Chem. Soc., 1972, 95, 5178. A comparison of other isomers and radicals, cations and anions: P. M. Mayer, M. S. Taylor, M. Wong, L. Radom, J. Phys. Chem. A, 1998, 102, 7074. Cyclopropylidene reaction H. F. Bettinger, P. R. Schreiner, P. v. R. Schleyer,

H.F. Schaefer, J. Phys. Chem., 1996, 100, 16147.

[68]Ref. [64, p. 157].

[69]Information supplied by Dr. R. Johnson of the National Institutes of Standards and Technology, USA (NIST): best fits to about 1100 vibrations of about 70 closed-shell molecules. An extensive collection of scaling factors is available on the NIST website (http://srdata.nist.gov/cccbdb/).

[70]A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100,16502.

[71]A. J. Holder and R. D. Dennington II, J. Mol. Struct. (Theochem), 1997, 401, 207.

[72]E. F. Healy and A. Holder, J. Mol. Struct. (Theochem), 1993, 281, 141.

[73]M. B. Cooligde, J. E. Marlin and J. J. P. Stewart, J. Comp. Chem., 1991, 12, 948.

[74]Ref. [58, pp. 74, 76–77, 80–82].

[75]A. C. Scheiner, J. Baker, and J. W. Andzelm, J. Comp. Chem., 1997, 18, 775.

[76]N. T. Anh, G. Frisson, A. Solladié-Cavallo, and P. Metzner, Tetrahedron, 1998, 54, 12841.

[77]G. Lendvay, J. Phys. Chem., 1994, 98, 6098.

[78]Available from Hypercube Inc., Gainsville, FL.

[79]Available for several kinds of computers from Gaussian Inc., Pittsburgh, PA.

[80]Gaussian 98, revision A.6, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stralmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keilh, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. Repogle, and J. A. Pople, Gaussian, Inc., Pittsburgh PA, 1998.