Semiempirical Calculations 341
functions that make up the MOs). The simple Hückel Fock matrix elements were simply relative energies 0 and –1 (0 and 
units, relative to the nonbonding level 
or in the EHM the Fock matrix elements were calculated from ionization energies. A single matrix diagonalization gave the energy levels and MO coefficients. This chapter is concerned with SE methods that are closer to the ab initio method in that the SCF procedure (sections 5.2.3.6d and 5.2.3.6e) is used to refine the energy levels and MO coefficients. As in ab initio calculations each Fock matrix element is calculated from a core integral 
density matrix elements 
and electron repulsion integrals (rs\tu), (ru\ts):
As stated above, the following discussion applies to SE methods that use the SCF procedure and so pay some service to Eq. (6.1). As with an ab initio calculation, to initiate the process we need an initial guess of the coefficients, to calculate the density matrix values 
the guess can come from a simple Hückel calculation (for a 
electron theory like the PPP method) or from an extended Hückel calculation (for an all-valence-electron theory, like CNDO and its descendants). The Fock matrix of 
elements is diagonalized repeatedly to refine energy levels and coefficients.
The divergence from the ab initio method lies in (1) treating only valence or
electrons, i.e. in the meaning of the “core,” (2) the mathematical functions used to expand the MOs (the basis set functions), (3) how the core and two-electron repulsion integrals are evaluated, and (4) the treatment of the overlap matrix. These approximations are discussed in detail by Dewar [7]. An excellent yet compact survey of the principles behind all the major SE methods is given by Levine [8], and SE methods have also been reviewed by Thiel [9]; a detailed exposition of the basic (pre-1970) theory behind these methods can be found in the book by Pople and Beveridge [10]. Expanding on points (1)–(4):
(1) Treating only valence or 
electrons, i.e. the meaning of the “core”. In an ab initio calculation 
is the kinetic energy of an electron moving in the force-field of the atomic nuclei, plus the potential energy of attraction of the electron to these atomic nuclei: the electron is moving under the influence of a positive core composed of atomic nuclei. SE calculations handle at most valence electrons (the PPP method handles only 
electrons), so each element of the core becomes an atomic nucleus plus its core electrons (for the PPP method, a nucleus with the core electrons plus all 
valence electrons). Instead of a cloud of all the electrons moving in a framework of nuclei, we have a cloud valence electrons (for the PPP method, 
electrons) moving in a framework of atomic cores (atomic core = nucleus + valence electrons, or for PPP, nucleus + all electrons that don’t contribute to the 
system). The SCF SE energy is calculated in a manner analogous to that of an ab initio calculation of the Hartree-Fock energy (cf. Eq. (5.149)), but n in Eq. (6.2) is not half the total number of electrons, but rather half the number of valence electrons (half the number of 
electrons for a PPP calculation), i.e. n is the number of MOs formed from the those electrons being included in the basis set. 
is the valence electronic 
electronic for the PPP method) energy, rather than the total electronic energy, and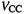 
is the core-core repulsion, rather than
342 Computational Chemistry
the nucleus–nucleus repulsion:
Treating the core electrons in effect as part of the atomic nuclei means that we need basis functions only for the valence electrons. With a minimal basis set (section 5.3.3) an ab initio calculation on ethene, 
needs five basis functions 
for each carbon and one basis function (1s) for each hydrogen, a total of 14 basis functions, while a SE calculation needs four functions for each carbon and one for each hydrogen, for a total of 12; for cholesterol, 
the numbers of basis functions are 181 and 154 for ab initio and SE, respectively. In both cases the SE calculation needs only about 85% as many basis functions as an ab initio calculation; the SE basis set advantage is small compared to minimal basis set ab initio calculations, but large compared to ab initio calculations with split valence and split valence plus polarization (section 5.3.3) basis sets. For ethene, comparing a 
ab initio calculation with a minimal basis SE calculation, the numbers of basis functions are 38 and 12, a ratio of 32%; for cholesterol, 497 and 154, a ratio of 31%. SE calculations use only a minimal basis set and hope to compensate for this by parameterization of the two-electron integrals (below).
(2) The basis set functions. In SE methods the basis functions correspond to atomic orbitals (valence AOs or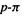 
AOs), while in ab initio calculations this is strictly true only for a minimal basis set, since an ab initio calculation can use many more basis functions than there are conventional AOs. The SCF-type SE methods we are considering in this chapter use Slater functions, rather than approximating Slater functions as sums of Gaussian functions (section 5.3.2). Recall that the only reason ab initio calculations use Gaussian, rather than the more accurate Slater, functions, is because calculation of the electron–electron repulsion two-electron integrals is far faster with Gaussian functions (section 5.3.2). In SE calculations these integrals have been parameterized into the
calculation (see below). Mathematical |
forms of the basis functions are still needed, |
to calculate overlap integrals |
for although these methods treat the overlap |
matrix as a unit matrix, some overlap integrals are evaluated (approximate MO theory has some apparent logical contradictions [7]) and used to help calculate core integrals and electron-repulsion integrals. As in ab initio calculations linear combinations of the basis functions are used to construct MOs, which in turn are multiplied by spin functions and used to represent the total molecular wavefunction as a Slater determinant (section 5.2.3.1).
(3) The integrals. The core integrals and the two-electron repulsion integrals (electron-repulsion integrals), Eq. (6.1), are not calculated from first principles (i.e. not from an explicit Hamiltonian and basis functions, as illustrated in section 5.2.3.6e), but rather many integrals are taken as zero, and those that are used are evaluated in an empirical way from the kinds of atoms involved and their distances apart. Recall that calculation of the two-electron integrals, particularly the threeand four-center ones (those involving three or four different atoms) takes up most of the time in an ab initio calculation. The integrals to be ignored (set equal to zero) are determined from the extent to which differential overlap is neglected. Differential overlap dS is the
Semiempirical Calculations 343
differential of the overlap integral (e.g. section 4.3.3) S:
SE methods differ amongst themselves in (amongst other ways) the criteria for setting dS = 0, i.e. for applying zero differential overlap (ZDO).
(4) The overlap matrix. SCF-type SE methods take the overlap matrix as a unit matrix, S = 1, so S vanishes from the Roothaan–Hall equations 
without the necessity of using an orthogonalizing matrix to transform these equations into standard eigenvalue form 
(which latter enables the Fock matrix to be diagonalized to give the MO coefficients and energy levels; sections 4.4.3, 4.4.1, and 5.2.3.6b).
6.2.2 The Pariser-Parr-Pople (PPP) method
The first SE SCF-type method to gain widespread use was the PPP method (1953) [11,12]. Like the SHM, PPP calculations are limited to 
electrons, with the other electrons forming a 
framework to hold the atomic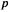 
orbitals in place. The Fock matrix elements are calculated from Eq. (6.1); for a PPP calculation 
represents the nuclei plus all non- 
-system electrons, 
is calculated from the coefficients of those p AOs contributing to 
and the two-electron repulsion integrals refer to electrons in the 
system. The one-center core integrals 
are estimated empirically from the ionization energy of a 2p AO and (see below) the two-electron integral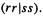 
The two-center core integrals 
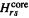are calculated from
where k is an empirical parameter chosen to give the best agreement with experiment of the wavelength of UV absorption bands, and the overlap integral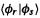 
is calculated from the basis functions, with the proviso that if 
and 
are on atoms that are not connected then the integral is taken as zero.
The two-electron integrals are evaluated by applying the ZDO approximation (above) to all different orbitals r and s:
From Eq. (6.6) and the definition of the two-electron integral
it follows that (1) for 
(rs|tu) = 0, and (2) for r =s and t = u, (rs|tu) = (rr|tt). Both cases are taken into account by writing