344 Computational Chemistry
where the 
are Kronecker deltas 
if the subscripts are the same, zero otherwise). Thus the four-center (i.e. 
and three-center (i.e. 
two-electron integrals are ignored, but not the two-center (i.e. 
and one-center (i.e. 
twoelectron integrals. The one-center integrals 
are taken as the difference between the valence-state ionization energy and the electron affinity of the atom bearing 
(these valence-state parameters refer to a hypothetical isolated atom in the same hybridization state as in the molecule, and can be found spectroscopically). The two-center integrals 
are estimated from 
and 
and the distance between the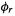 
and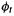 
atoms. |
|
|
|
Although the overlap integrals |
are actually calculated for the evaluation of |
||
(Eq. (6.5), the overlap matrix is taken as a unit matrix as far as the matrix |
|||
Roothaan–Hall equations |
go; thus |
or |
and the |
Fock matrix is diagonalized to give the MO coefficients and energy levels without transforming it with an orthogonalizing matrix. That the overlap matrix is a unit matrix is a corollary of the ZDO approximation of Eq. (6.6), from which it follows that the off-diagonal matrix elements are zero; the diagonal elements are of course unity
if normalized |
AO basis functions |
are used. PPP energies are electronic |
||
energies |
or electronic energies |
plus core-core repulsions, |
if |
is added |
(Eq. (6.2)). |
|
|
|
|
The PPP method has been used to calculate the UV spectra of conjugated compounds, especially dyes [13], a task it performs fairly well. The accuracy of these calculations can be improved by incorporating electron correlation (section 5.4), using the configuration interaction (CI) method. The calculations were usually done at a fixed geometry, although an empirical bond length-bond order relation permits optimization of bond length. The classical PPP method is not much used, having evolved into other neglect of differential overlap (NDO) methods, especially those parameterized for spectra, like INDO/S and ZINDO/S (below).
6.2.3 The complete neglect of differential overlap (CNDO) method
The first SE SCF-type method to go beyond just 
electrons was the complete neglect of differential overlap method (1965) [14]. This was a general-geometry method, since it is not limited to planar 
systems (molecules with conjugated 
electron systems, like benzene, are usually planar). Like the other early general-geometry method, the EHM, which appeared in 1963 (section 4.4), CNDO calculations use a minimal valence basis set of Slater-type orbitals, in which each atom has the usual number of valence AOs. The Fock matrix elements are calculated from Eq. (6.1); for a CNDO calculation 
represents the nuclei plus all core electrons, 
is calculated from the coefficients of the valence AOs, and the two-electron repulsion integrals refer to valence electrons.
There are two versions of CNDO, CNDO/1 and an improved version, CNDO/2. First
look at CNDO/1. Consider the core integrals |
where both orbitals are the same |
|
(i.e. the same orbital occurs twice in the integral |
|
and are on the |
same atom A. Recall the example of an ab initio calculation on |
(section 5.2.36e). |
|
Semiempirical Calculations 345
Consider, say, element (1,1) of that 
matrix. From Eq. (5.116):
Eq. (6.9) can be generalized to a matrix element (r,r) and a molecule with atoms A, B, C,..., giving
where 
is a basis function on atom A. The 
term in Eq. (7.0) is regarded as the energy of an electron in the AO on A corresponding to the function 
and is taken as the negative of the valence-state ionization energy of such an electron. The integrals in the 
term are simply calculated as the potential energy of a valence s orbital in the electrostatic field of the core of atom A, B, etc., e.g.
where 
is the charge on the core of atom B, i.e. the atomic number minus the number of core (non-valence) electrons, and the variable 
is the distance of the 2s electron from the center of the core (from the atomic nucleus). The core integrals with different orbitals 
on the same atom (A = B; one-center integrals) or on different atoms are taken as being proportional to the overlap integral of the relevant orbitals:
The overlap integral here is calculated from the basis functions, although (as for the PPP method, above) the overlap matrix is taken as a unit matrix as far as the matrix Roothaan–Hall equations are concerned. The proportionality constant 
is taken as the arithmetic mean of parameters for atoms A and B, these parameters being those that give the best fit of CNDO MO coefficients to those of minimal-basis-set ab initio calculations. Since different AOs on the same atom are orthogonal, when A=B these integrals are zero. Note thatcalculating 
from a best-fit to minimal-basis-set ab initio calculations means that CNDO parameterization is not purely empirical, but rather, to some extent attempts to match (low-level) ab initio results. This is a weakness of CNDO and a potential weakness of its successors INDO and NDDO (below). As repeatedly emphasized by Dewar, this deficiency was avoided in his methods (section 6.2.5.1) by consistently parameterizing to match experiment.
As with the PPP method, the two-electron repulsion integrals are evaluated by applying the ZDO approximation to all different orbitals r and s (Eq. (6.6)). Thus the two-electron integrals reduce to 
(Eq. (6.8)), i.e. only oneand two-center two-electron integrals are considered. All one-center integrals on the