5.5.5Miscellaneous properties – UV and NMR spectra, ionization energies, and electron affinities

Ab initio calculations 313

UV spectra

Ultraviolet spectra result from the promotion of an electron in an occupied MO of a ground electronic state molecule into a virtual MO, thus forming an electronically excited state [152] (excited state-to-excited state spectra are not normally studied by experimentalists). Calculation of UV spectra with reasonable accuracy requires some method of dealing with excited states. Simply equating energy differences between HOMO and LUMO with 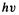does not give satisfactory results for the absorption frequency/wavelength, because the energy of a virtual orbital, unlike that of an occupied one, is not a good measure of its energy (of the energy needed to remove an electron from it; this is dealt with in connection with ionization potentials and electron affinities) and because this method ignores the energy difference between a singlet and a triplet state.

Electronic spectra of moderate accuracy can be calculated by the configuration interaction CIS method (section 5.4.3) [173]. Compare, for example, the UV spectra of methylenecyclopropene calculated by the CIS/6-31+G* method (diffuse functions appear to be desirable in treating excited states, as the electron cloud is relatively extended) with the experimental spectrum [173], in Table 5.20. The agreement in wavelength is not particularly good for the longest-wavelength band, although this result can be made more palatable by noting that both calculation and experiment agree reasonably well on relative intensities (the two bands that were not observed are calculated to be relatively weak and to lie very near the strongest band). The CIS approach to excited states has been said [173] to be analogous to the HF approach to ground states in that both give at least qualitatively useful results.

NMR spectra

NMR spectra result from the transition of an atomic nucleus in a magnetic field from a low-energy to a high-energy state [152]. Quantum-mechanical calculations of NMR spectra focus on predicting the chemical shift (magnetic field strength needed for the transition relative to that needed for some reference) of a nucleus. This requires calculation of the magnetic shielding of the nuclei of the molecule of interest, and of the reference nuclei, usually those of tetramethylsilane, TMS. The chemical shift of the

314 Computational Chemistry

or nucleus is then its (absolute) shielding value minus that of the TMS or nucleus. The theory of magnetic shielding of nuclei involves a treatment of how the energy of a nucleus varies with a magnetic field and with nuclear magnetic moments [174]. NMR spectra can be calculated with remarkable accuracy even at the HF level [175] (although there is some evidence that improved results are obtained using the

Ab initio calculations 315

MP2 method [175b,176]), as is clearly shown by the results in Fig. 5.44. The remarkable shielding effect of a benzene ring in [7]paracyclophane [177] is nicely reproduced. The calculation of NMR spectra has become an important tool in probing the electronic structure of theoretically interesting molecules [178],

Ionization energies and electron affinities

Ionization energies (also called ionization potentials) and electron affinities are related in that both involve transfer of an electron between a molecular orbital and infinity: in one case (IE) we have removal of an electron from an occupied orbital and in the other (EA) addition of an electron to a virtual (or a half-occupied) orbital. The IE for an orbital is defined as the energy needed to remove an electron from the orbital (to infinite separation), while the EA of an orbital is the energy released when the orbital accepts an electron from infinity [179]. The term IE when applied to a molecule normally means the minimum energy needed to remove an electron to infinity, i.e. to form the radical (for an originally closed-shell molecule) cation, and the term electron affinity normally means the maximum energy released when the molecule accepts an electron to form the radical anion (for an originally closed-shell molecule). The IE of a “stable” species, i.e. any molecule or atom that can exist (a relative minimum on the potential energy surface), is always positive. The EA of a molecule is positive if the accepted electron is bound, i.e. if it is not spontaneously ejected; if the new electron is ejected in microseconds or less (is unbound), the molecule has a negative EA (is a “resonance state” – this has nothing to do with the term resonance as in resonance hybrid).

IEs and EAs may be vertical or adiabatic: the energy difference between the precursor molecule and the species formed by removing or adding an electron gives the vertical value if is at the same geometry as while the adiabatic value is obtained if has its own actual, equilibrium geometry. Since the equilibrium geometry of is clearly of lower energy than the unrelaxed geometry corresponding to vertical IEs are larger than adiabatic IEs, and vertical EAs are smaller than adiabatic EAs. Experimental IEs and EAs may be vertical or adiabatic. The adiabatic values appear to be of more interest to chemists, since it is these that represent the energy difference between two “stable” molecules (the neutral and the charged; at least in those cases where the charged species does not instantly decompose), but compilations of IEs and EAs often do not state explicitly whether their listed values are adiabatic or vertical; a welcome exception is the book by Levin and Lias [ 180]. A good brief discussion of IEs and EAs, including various measurement techniques, is to be found in the compilation by Lias et al. [130b]. Many IEs and EAs are available on the worldwide web [130a].

lonization energies and electron affinities can be calculated simply as the energy difference between the neutral and the ion. Approximate IEs can be obtained by applying Koopmans’ (not Koopman’s) theorem [181], which says that the energy required to remove an electron from an orbital is the negative of the orbital energy. Thus the IE of a molecule is approximately the negative of the energy of its HOMO (the principle does not work as well for ionization ofelectrons more tightly bound than those in the HOMO). This makes it simple to obtain approximate IEs for comparison with photoelectron spectroscopy [182] results. Unfortunately, the principle does not work well for EAs: the EA of a molecule is not reasonably well approximated as the negative of the LUMO energy. In fact, ab initio calculations normally give virtual MOs (vacant MOs) positive