272 Computational Chemistry

using HF/6-31G* energies (this level appears to be the lowest for which reasonably accurate results can usually be expected [114]), employing the unrestricted HF(UHF, i.e. UHF/6-31G*; end of section 5.2) method for the two radicals:

So E(C–O) = E(C–C) – E(iso) = 368 – 36.9 =

Now let us repeat this calculation using MP2(FC)/6 – 21G* energies:

So

E(C–O) = E(C–C) – E(iso) = 368 – (–4.4) =

In the HF case E(iso) is 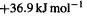and in the MP2 case it is 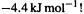Thus E(C–O) comes out in one case significantly weaker than E(C–C), and in the other case slightly stronger. The experimental C–O bond energy for has been reported as [115]. Clearly, at the HF/6-31G* level anyway, this approach to bond energies is unreliable, but may be viable at the MP2 level [116].

Isodesmic reactions help us to make the most of the method/basis set we decide to use(this decision being guided by the size of the molecules and the computational resources available, i.e. by how “expensive” the calculations are). They have on occasion being used with fairly high-level calculations, to obtain high-quality results that would require even higher-level methods were “direct-subtraction” methods to be used [117]. Isodesmic reactions have been discussed and used extensively [109,118].

5.5.2.2b Thermodynamics; high-accuracy calculations

As the previous discussion suggests (section 5.5.2.2a), the calculation of good relative energies is much more challenging than the calculation of good geometries. Nevertheless, it is now possible to reliably calculate energy differences to within about An energy difference with an error of 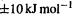is said to be within chemical accuracy. The term was popularized by Pople (biographical footnote section 5.3.3) in connection with the G1 and G2 (see below) methods. An accuracy of about commonly rounded in this context to was, in 1991, considered to be realistic and chemically useful, perhaps because this is small compared to typical bond energies (roughly 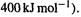The ab initio energies and methods needed for results ofchemical accuracy are called high-accuracy energies and methods.

As one might expect, high-accuracy energy methods are based on high-level correlational methods and big basis sets. However, because the straightforward application of such computational levels would require unreasonable times (be very “expensive”),

Ab initio calculations 273

the calculations are broken up into several steps, each of which provides an energy value; summing these gives an energy close to that which would be obtained from the more unwieldy one-step calculation. There are two classes of popular high-accuracy energy methods: the Pople group’s G2 and G3 (for Gaussian-2 and Gaussian-3; these have superseded Gaussian-1) methods and their variants, and the Peterson group’s CBS (complete basis set) methods. These will now be discussed and briefly compared.

The G2 method and its variants

The G2 and G3 methods [119] are the successors to the first widely-used high-accuracy energy method, the G1 method [120], which they have replaced. Relatively few results are yet available for the G3 method, so only G2 calculations will be discussed. These consist of nine steps:

1.An HF/6-31G* geometry optimization.

2.An HF/6-31G* ZPE calculation.

3.An MP2(full)/6-31G* optimization(at the time G1 and G2 were being developed, analytic frequencies were not available for MP2(FC) (section 5.4.2) optimizations, which are faster and about as good).

4.An MP4/6-311G** single-point calculation.

5.An MP4/6-311 + G** single-point calculation.

6.An MP4/6-311G(2df,p) single-point calculation.

7.A QCISD(T)/6-311G** single-point calculation.

8.An MP2/6-311 + G(3df,2p) single-point calculation.

9.An empirical higher-level correction (HLC) to account for any remaining errors due to electron correlation.

The tedious procedure for combining these steps to get the G2 energy is detailed by Foresman and Frisch [ 121 ], but with the Gaussian 94 and 98 programs only the keyword “G2” is needed. A G2 calculation is essentially equivalent to a QCISD(T)/6-311 + G(3df,2p) calculation on an MP2(full)/6-31G* geometry with a HF/6-31G* ZPE correction [122]. Because of the empirical HLC the G2 method is semiempirical, except when this correction cancels out. This happens, for example, in calculating proton affinities as the energy difference of the protonated and unprotonated species [123]. The HLC is based on the number of and spin electrons, which are the same for both species in a case like this. The G2 method is among the most time-consuming of the high-accuracy energy methods, and several variants have been developed with a view to getting greater speed with little loss of accuracy. This has been largely achieved with the G2(MP2) and G2(MP2,SVP) (SVP = split valence plus polarization basis set) methods. Actually, in the absence of any evidence to the contrary, one may now assume that the G3 method, which seems to be somewhat more accurate and faster than G2, is the Gaussian high-accuracy method of choice, and this, or a faster but nearly as accurate variation, like G3(MP2), is recommended over the G2 family.

274 Computational Chemistry

CBS methods

Complete basis set methods [86] involve essentially seven or eight steps:

2.A ZPE calculation at the optimization level.

3.An HF single-point calculation with a very big basis set (6-311 + G(3d2f, 2df, p) or 6-311+ G(3d2f, 2df, 2p), depending on the particular CBS method).

4.An MP2 single-point calculation (basis depending on the particular CBS method).

5.Something called a pair natural orbital extrapolation to estimate the error due to using a finite basis set.

6.An MP4 single-point calculation.

7.For some CBS methods, a QCISD(T) single-point calculation.

8.One or more empirical corrections.

There are three basic CBS methods: CBS-4 (for fourth-order extrapolation), CBS-Q (for quadratic CI) and CBS-APNO (or CBS-QCI/APNO, for asymptotic pair natural orbitals), in order of increasing accuracy (and increasing computer time). These methods are available with keywords in the Gaussian 94 and 98 programs.

Comparison of G2-type and CBS methods

The relative merits of the four most popular G2 and CBS methods are apparent from Table 5.10 (taken from the book by Foresman and Frisch [1e]). All four methods are available as a keyword in Gaussian 94 and Gaussian 98. If the test sample is representative, then the CBS-Q method is the most accurate and the G2 the second most accurate (G3 should be somewhat better and faster than G2). As CBS-Q seems to be faster than G2, CBS-Q appears to be the method of choice among these four for most high accuracy energy calculations, unless the system is relatively large, in which case CBS-4, the least accurate of the four, may have to be used. G3 and CBS-Q likely have quite similar errors, and G3 is faster than G2: the times on a Pentium 3