
- •COMPUTATIONAL CHEMISTRY
- •CONTENTS
- •PREFACE
- •1.1 WHAT YOU CAN DO WITH COMPUTATIONAL CHEMISTRY
- •1.2 THE TOOLS OF COMPUTATIONAL CHEMISTRY
- •1.3 PUTTING IT ALL TOGETHER
- •1.4 THE PHILOSOPHY OF COMPUTATIONAL CHEMISTRY
- •1.5 SUMMARY OF CHAPTER 1
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •2.1 PERSPECTIVE
- •2.2 STATIONARY POINTS
- •2.3 THE BORN–OPPENHEIMER APPROXIMATION
- •2.4 GEOMETRY OPTIMIZATION
- •2.6 SYMMETRY
- •2.7 SUMMARY OF CHAPTER 2
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •3.1 PERSPECTIVE
- •3.2 THE BASIC PRINCIPLES OF MM
- •3.2.1 Developing a forcefield
- •3.2.2 Parameterizing a forcefield
- •3.2.3 A calculation using our forcefield
- •3.3 EXAMPLES OF THE USE OF MM
- •3.3.2 Geometries and energies of polymers
- •3.3.3 Geometries and energies of transition states
- •3.3.4 MM in organic synthesis
- •3.3.5 Molecular dynamics and Monte Carlo simulations
- •3.4 GEOMETRIES CALCULATED BY MM
- •3.5 FREQUENCIES CALCULATED BY MM
- •3.6 STRENGTHS AND WEAKNESSES OF MM
- •3.6.1 Strengths
- •3.6.2 Weaknesses
- •3.7 SUMMARY OF CHAPTER 3
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •4.1 PERSPECTIVE
- •4.2.1 The origins of quantum theory: blackbody radiation and the photoelectric effect
- •4.2.2 Radioactivity
- •4.2.3 Relativity
- •4.2.4 The nuclear atom
- •4.2.5 The Bohr atom
- •4.2.6 The wave mechanical atom and the Schrödinger equation
- •4.3.1 Introduction
- •4.3.2 Hybridization
- •4.3.3 Matrices and determinants
- •4.3.4 The simple Hückel method – theory
- •4.3.5 The simple Hückel method – applications
- •4.3.6 Strengths and weaknesses of the SHM
- •4.4.1 Theory
- •4.4.2 An illustration of the EHM: the protonated helium molecule
- •4.4.3 The extended Hückel method – applications
- •4.4.4 Strengths and weaknesses of the EHM
- •4.5 SUMMARY OF CHAPTER 4
- •REFERENCES
- •EASIER QUESTIONS
- •5.1 PERSPECTIVE
- •5.2.1 Preliminaries
- •5.2.2 The Hartree SCF method
- •5.2.3 The HF equations
- •5.2.3.1 Slater determinants
- •5.2.3.2 Calculating the atomic or molecular energy
- •5.2.3.3 The variation theorem (variation principle)
- •5.2.3.4 Minimizing the energy; the HF equations
- •5.2.3.5 The meaning of the HF equations
- •5.2.3.6a Deriving the Roothaan–Hall equations
- •5.3 BASIS SETS
- •5.3.1 Introduction
- •5.3.2 Gaussian functions; basis set preliminaries; direct SCF
- •5.3.3 Types of basis sets and their uses
- •5.4 POST-HF CALCULATIONS: ELECTRON CORRELATION
- •5.4.1 Electron correlation
- •5.4.3 The configuration interaction approach to electron correlation
- •5.5.1 Geometries
- •5.5.2 Energies
- •5.5.2.1 Energies: Preliminaries
- •5.5.2.2 Energies: calculating quantities relevant to thermodynamics and to kinetics
- •5.5.2.2a Thermodynamics; “direct” methods, isodesmic reactions
- •5.5.2.2b Thermodynamics; high-accuracy calculations
- •5.5.2.3 Thermodynamics; calculating heats of formation
- •5.5.2.3a Kinetics; calculating reaction rates
- •5.5.2.3b Energies: concluding remarks
- •5.5.3 Frequencies
- •Dipole moments
- •Charges and bond orders
- •Electrostatic potential
- •Atoms-in-molecules
- •5.5.5 Miscellaneous properties – UV and NMR spectra, ionization energies, and electron affinities
- •5.5.6 Visualization
- •5.6 STRENGTHS AND WEAKNESSES OF AB INITIO CALCULATIONS
- •5.7 SUMMARY OF CHAPTER 5
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •6.1 PERSPECTIVE
- •6.2 THE BASIC PRINCIPLES OF SCF SE METHODS
- •6.2.1 Preliminaries
- •6.2.2 The Pariser-Parr-Pople (PPP) method
- •6.2.3 The complete neglect of differential overlap (CNDO) method
- •6.2.4 The intermediate neglect of differential overlap (INDO) method
- •6.2.5 The neglect of diatomic differential overlap (NDDO) method
- •6.2.5.2 Heats of formation from SE electronic energies
- •6.2.5.3 MNDO
- •6.2.5.7 Inclusion of d orbitals: MNDO/d and PM3t; explicit electron correlation: MNDOC
- •6.3 APPLICATIONS OF SE METHODS
- •6.3.1 Geometries
- •6.3.2 Energies
- •6.3.2.1 Energies: preliminaries
- •6.3.2.2 Energies: calculating quantities relevant to thermodynamics and kinetics
- •6.3.3 Frequencies
- •6.3.4 Properties arising from electron distribution: dipole moments, charges, bond orders
- •6.3.5 Miscellaneous properties – UV spectra, ionization energies, and electron affinities
- •6.3.6 Visualization
- •6.3.7 Some general remarks
- •6.4 STRENGTHS AND WEAKNESSES OF SE METHODS
- •6.5 SUMMARY OF CHAPTER 6
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •7.1 PERSPECTIVE
- •7.2 THE BASIC PRINCIPLES OF DENSITY FUNCTIONAL THEORY
- •7.2.1 Preliminaries
- •7.2.2 Forerunners to current DFT methods
- •7.2.3.1 Functionals: The Hohenberg–Kohn theorems
- •7.2.3.2 The Kohn–Sham energy and the KS equations
- •7.2.3.3 Solving the KS equations
- •7.2.3.4a The local density approximation (LDA)
- •7.2.3.4b The local spin density approximation (LSDA)
- •7.2.3.4c Gradient-corrected functionals and hybrid functionals
- •7.3 APPLICATIONS OF DENSITY FUNCTIONAL THEORY
- •7.3.1 Geometries
- •7.3.2 Energies
- •7.3.2.1 Energies: preliminaries
- •7.3.2.2 Energies: calculating quantities relevant to thermodynamics and kinetics
- •7.3.2.2a Thermodynamics
- •7.3.2.2b Kinetics
- •7.3.3 Frequencies
- •7.3.6 Visualization
- •7.4 STRENGTHS AND WEAKNESSES OF DFT
- •7.5 SUMMARY OF CHAPTER 7
- •REFERENCES
- •EASIER QUESTIONS
- •HARDER QUESTIONS
- •8.1 FROM THE LITERATURE
- •8.1.1.1 Oxirene
- •8.1.1.2 Nitrogen pentafluoride
- •8.1.1.3 Pyramidane
- •8.1.1.4 Beyond dinitrogen
- •8.1.2 Mechanisms
- •8.1.2.1 The Diels–Alder reaction
- •8.1.2.2 Abstraction of H from amino acids by the OH radical
- •8.1.3 Concepts
- •8.1.3.1 Resonance vs. inductive effects
- •8.1.3.2 Homoaromaticity
- •8.2 TO THE LITERATURE
- •8.2.1 Books
- •8.2.2 The Worldwide Web
- •8.3 SOFTWARE AND HARDWARE
- •8.3.1 Software
- •8.3.2 Hardware
- •8.3.3 Postscript
- •REFERENCES
- •INDEX

164 Computational Chemistry
If switching the coordinates of two of the particles leaves the function unchanged, it is said to be symmetric with respect to particle exchange, while if the function changes sign it is said to be antisymmetric with respect to particle exchange. Comparing the predictions of theory with the results of experiment shows [5] that electronic wavefunctions are actually antisymmetric with respect to exchange (such particles are called fermions, after the physicist Enrico Fermi; particles like photons whose wavefunctions are exchange-symmetric are called bosons, after the physicist S. Bose). Any rigorous attempt to approximate the wavefunction should use an antisymmetric function of the coordinates of the electrons 1 , 2 , . . . . n, but the Hartree product is symmetric rather than antisymmetric; e.g. if we approximate a helium atom wavefunction as the product of two hydrogen atom 1s orbitals, then if
should use an antisymmetric function of the coordinates of the electrons 1 , 2 , . . . . n, but the Hartree product is symmetric rather than antisymmetric; e.g. if we approximate a helium atom wavefunction as the product of two hydrogen atom 1s orbitals, then if  and
and  then
then 
These defects of the Hartree SCF method were corrected by Fock (section 4.3.4) and by Slater2 in 1930 [6], and Slater devised a simple way to construct a total wavefunction  from one-electron functions (i.e. orbitals) such that
from one-electron functions (i.e. orbitals) such that  will be antisymmetric to electron switching. Hartree’s iterative, average-field approach supplemented with electron
will be antisymmetric to electron switching. Hartree’s iterative, average-field approach supplemented with electron
spin and antisymmetry leads to the HF equations.
5.2.3The HF equations
5.2.3.1Slater determinants
The Hartree wavefunction (above) is a product of one-electron functions called orbitals, or, more precisely, spatial orbitals: these are functions of the usual space coordinates x, y, z. The Slater wavefunction is composed, not just of spatial orbitals, but of spin orbitals. A spin orbital  (spin) is the product of a spatial orbital and a spin function,
(spin) is the product of a spatial orbital and a spin function,
or |
The spin orbitals corresponding to a given spatial orbital are |
|
|
|
|
and |
|
As the function |
(spatial) has as its variables the coordinates x, y, z, |
so the spin func- |
|
tions |
and have as their variables a spin coordinate, sometimes denoted (Greek |
||
letter |
or |
or (Greek omega). We know that a wavefunction |
fits in with an |
operator and eigenvalues, say the energy operator and energy eigenvalues, according
to the equation |
|
Analogously, the spin functions and are associated |
|
with the spin operator |
according to |
and |
|
Unlike most other functions, then, and |
each have only one eigenvalue, |
||
and |
respectively. A spin function has the peculiar property that it is zero |
||
unless |
spin function) or |
spin function). A function that is zero |
|
everywhere except at one value of its variable, where it spikes sharply, is a delta function
2John Slater, born Oak Park Illinois, 1900. Ph.D. Harvard, 1923. Professor of physics, Harvard, 1924– 1930; MIT 1930–1966; University of Florida at Gainesville, 1966–1976. Author of 14 textbooks, contributed to solid-state physics and quantum chemistry, developed X-alpha method (early density functional theory method). Died Sanibel Island, Florida, 1976.

Ab initio calculations 165
(invented by Dirac – section 4.2.3). Since the spin function  (spin
(spin  or
or  ) describing
) describing
an electron exists only when the spin variable |
these two values can be con- |
|
sidered the allowed values of the spin quantum number |
mentioned in section 4.2.6. |
|
Sometimes an electron with spin quantum number |
(“an electron with spin |
is |
called an  electron, and said to have up spin, and an electron with spin
electron, and said to have up spin, and an electron with spin  is called a
is called a electron, and said to have down spin. Up and down electrons are often denoted by arrows
electron, and said to have down spin. Up and down electrons are often denoted by arrows  and
and  respectively. A nice, brief treatment of the delta function and of the mathematical treatment of the spin functions is given by Levine [7].
respectively. A nice, brief treatment of the delta function and of the mathematical treatment of the spin functions is given by Levine [7].
The Slater wavefunction differs from the Hartree function not only in being composed of spin orbitals rather than just spatial orbitals, but also in the fact that it is not a simple product of one-electron functions, but rather a determinant (section 4.3.3) whose elements are these functions. To construct a Slater wavefunction (Slater determinant) for a closed-shell species (the only kind we consider in any detail here), we use each of the occupied spatial orbitals to make two spin orbitals, by multiplying the spatial orbital by  and, separately, by
and, separately, by  The spin orbitals are then filled with the available electrons. An example should make the procedure clear (Fig. 5.2). Suppose we wish to write a Slater determinant for a four-electron closed-shell system. We need two spatial molecular orbitals, since each can hold a maximum of two electrons; each spatial orbital
The spin orbitals are then filled with the available electrons. An example should make the procedure clear (Fig. 5.2). Suppose we wish to write a Slater determinant for a four-electron closed-shell system. We need two spatial molecular orbitals, since each can hold a maximum of two electrons; each spatial orbital
(spatial) is used to make two spin orbitals,  (spatial)
(spatial) and
and (spatial)
(spatial) (alternatively, each spatial orbital could be thought of as a composite of two spin orbitals, which we are separating and using to build the determinant). Along the first (top) row of a determinant we write successively the first
(alternatively, each spatial orbital could be thought of as a composite of two spin orbitals, which we are separating and using to build the determinant). Along the first (top) row of a determinant we write successively the first spin orbital, the first spin orbital, the second
spin orbital, the first spin orbital, the second  spin orbital, and the second
spin orbital, and the second  spin orbital, using up our occupied spatial (and thus spin) orbitals. Electron one is then assigned to all four spin orbitals of the first row – in a sense it is allowed to roam among these four spin orbitals [8]. The second row of
spin orbital, using up our occupied spatial (and thus spin) orbitals. Electron one is then assigned to all four spin orbitals of the first row – in a sense it is allowed to roam among these four spin orbitals [8]. The second row of

166 Computational Chemistry
the determinant is the same as the first, except that it refers to electron two rather than electron one; likewise the third and fourth rows refer to electrons three and four, respectively. The result is the determinant of Eq. (5.10).
(The  factor ensures that the wavefunction is normalized, i.e. that
factor ensures that the wavefunction is normalized, i.e. that  integrated over all space= 1 [9].) This Slater determinant ensures that there are no more than two electrons in each spatial orbital, since for each spatial orbital there are only two one-electron spin functions, and it ensures that
integrated over all space= 1 [9].) This Slater determinant ensures that there are no more than two electrons in each spatial orbital, since for each spatial orbital there are only two one-electron spin functions, and it ensures that  is antisymmetric since switching two electrons amounts to exchanging two rows of the determinant, and this changes its sign (section 4.3.3). Note that instead of assigning the electrons successively to row 1, row 2, etc., we could have placed them in column 1, column 2,
is antisymmetric since switching two electrons amounts to exchanging two rows of the determinant, and this changes its sign (section 4.3.3). Note that instead of assigning the electrons successively to row 1, row 2, etc., we could have placed them in column 1, column 2,  of Eq. (5.11) =
of Eq. (5.11) = of Eq. (5.10). Some authors use the row format for the electrons, others the column format.
of Eq. (5.10). Some authors use the row format for the electrons, others the column format.
Slater determinants enforce the Pauli exclusion principle, which forbids any two electrons in a system to have all quantum numbers the same. This is readily seen for an atom: if the three quantum numbers n, l and  of
of  (x, y, z) (section 4.2.6) and the spin quantumnumber
(x, y, z) (section 4.2.6) and the spin quantumnumber 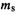 of
of  or
or  were all the same for any electron, two rows (or columns, in the alternative formulation) would be identical and the determinant, hence the wavefunction, would vanish (section 4.3.3).
were all the same for any electron, two rows (or columns, in the alternative formulation) would be identical and the determinant, hence the wavefunction, would vanish (section 4.3.3).
For 2n electrons (we are limiting ourselves for now to even-electron species, as the theory for these is simpler) the general form of a Slater determinant is clearly the 2n × 2n determinant
The Slater determinant for the total wavefunction  of a 2n-electron atom or molecule is a 2n × 2n determinant with 2n rows due to the 2n electrons and 2n columns due to the 2n spin orbitals (you can interchange the row/column format); since these are closed-shell species, the number of spatial orbitals
of a 2n-electron atom or molecule is a 2n × 2n determinant with 2n rows due to the 2n electrons and 2n columns due to the 2n spin orbitals (you can interchange the row/column format); since these are closed-shell species, the number of spatial orbitals  is half the number of electrons. We use the lowest n occupied spatial orbitals (the lowest 2n spin orbitals) to make the determinant.
is half the number of electrons. We use the lowest n occupied spatial orbitals (the lowest 2n spin orbitals) to make the determinant.

Ab initio calculations 167
The determinant (= total molecular wavefunction  ) just described will lead to (remainder of section 5.2) n occupied, and a number of unoccupied, component spatial molecular orbitals
) just described will lead to (remainder of section 5.2) n occupied, and a number of unoccupied, component spatial molecular orbitals  These orbitals
These orbitals  from the straightforward Slater determinant are called canonical (in mathematics the word means “in simplest or standard form”) molecular orbitals. Since each occupied spatial
from the straightforward Slater determinant are called canonical (in mathematics the word means “in simplest or standard form”) molecular orbitals. Since each occupied spatial  can be thought of as a region of space which accommodates a pair of electrons, we might expect that when the shapes of these orbitals are displayed (“visualized”; section 5.5.6) each one would look like a bond or a lone pair. However, this is often not the case; e.g. we do not find that one of the canonical MOs of water connects the O with one H, and another canonical MO connects the O with another H. Instead most of these MOs are spread over much of a molecule – delocalized (lone pairs, unlike conventional bonds, do tend to stand out). However, it is possible to combine the canonical MOs to get localized MOs which look like our conventional bonds and lone pairs. This is done by using the columns (or rows) of the Slater
can be thought of as a region of space which accommodates a pair of electrons, we might expect that when the shapes of these orbitals are displayed (“visualized”; section 5.5.6) each one would look like a bond or a lone pair. However, this is often not the case; e.g. we do not find that one of the canonical MOs of water connects the O with one H, and another canonical MO connects the O with another H. Instead most of these MOs are spread over much of a molecule – delocalized (lone pairs, unlike conventional bonds, do tend to stand out). However, it is possible to combine the canonical MOs to get localized MOs which look like our conventional bonds and lone pairs. This is done by using the columns (or rows) of the Slater  to create a
to create a  with modified columns (or rows): if a column/row of a determinant is multiplied by k and added to another column/row, the determinant is unchanged (section 4.3.3). We see that if this is applied to the Slater determinant, we will get a “new” determinant corresponding to exactly the same total wavefunction, i.e. to the same molecule, but built up from different component occupied MOs
with modified columns (or rows): if a column/row of a determinant is multiplied by k and added to another column/row, the determinant is unchanged (section 4.3.3). We see that if this is applied to the Slater determinant, we will get a “new” determinant corresponding to exactly the same total wavefunction, i.e. to the same molecule, but built up from different component occupied MOs  The new
The new and the new
and the new  are no less or more correct than the previous ones, but by appropriate manipulation of the columns/rows the
are no less or more correct than the previous ones, but by appropriate manipulation of the columns/rows the  can be made to correspond to our ideas of bonds and lone pairs. These localized MOs are sometimes useful.
can be made to correspond to our ideas of bonds and lone pairs. These localized MOs are sometimes useful.
5.2.3.2Calculating the atomic or molecular energy
The next step in deriving the HF equations is to express the energy of the molecule or atom in terms of the total wavefunction the energy will then be minimized with respect to each of the component molecular (or atomic; an atom is a special case of a molecule) spin orbitals
the energy will then be minimized with respect to each of the component molecular (or atomic; an atom is a special case of a molecule) spin orbitals  and
and  (cf. the minimization of energy with respect to basis function coefficients in section 4.3.3). The derivation of these equations involves considerable algebraic manipulation, which is at times hard to follow without actually writing out the intermediate expressions. The procedure has been summarized by Pople and Beveridge [10], and a less condensed account is given by Lowe [11].
(cf. the minimization of energy with respect to basis function coefficients in section 4.3.3). The derivation of these equations involves considerable algebraic manipulation, which is at times hard to follow without actually writing out the intermediate expressions. The procedure has been summarized by Pople and Beveridge [10], and a less condensed account is given by Lowe [11].
It follows from the Schrödinger equation that the energy of a system is given by
This is similar to Eq. (4.40) in chapter 4, but here the total wavefunction  has been specified, and allowance has been made for the possibility of
has been specified, and allowance has been made for the possibility of  being a complex function by utilizing its complex conjugate
being a complex function by utilizing its complex conjugate  this ensures that E, the energy of the atom or molecule, will be real. If
this ensures that E, the energy of the atom or molecule, will be real. If  is complex then
is complex then  will not be a real number, while
will not be a real number, while  will, as must be the case for a probability. Integration is with respect to three spatial coordinates and one spin coordinate, for each electron. This is symbolized by
will, as must be the case for a probability. Integration is with respect to three spatial coordinates and one spin coordinate, for each electron. This is symbolized by  which means dx dy dz d
which means dx dy dz d  so for a 2n-electron system these integrals are actually 4 × 2n-fold, each electron having its set of four coordinates. We assume the use of orthonormal functions (section 4.3.4), since this makes several integrals disappear in the derivation of the energy. Working with the
so for a 2n-electron system these integrals are actually 4 × 2n-fold, each electron having its set of four coordinates. We assume the use of orthonormal functions (section 4.3.4), since this makes several integrals disappear in the derivation of the energy. Working with the

168 Computational Chemistry
usual normalized wavefunctions makes the denominator unity, and Eq. (5.13) can then be written as
or using the more compact Dirac notation for integrals (section 4.4.1)
In Eq. (5.14) it is understood that the first  is actually
is actually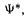 and that the integration variables are the space and spin coordinates. The vertical bars are only to visually separate the operator from the two functions, for clarity.
and that the integration variables are the space and spin coordinates. The vertical bars are only to visually separate the operator from the two functions, for clarity.
We next substitute into Eq. (5.14) the Slater determinant for  (and
(and  and the explicit expression for the Hamiltonian. A simple extension of the helium Hamiltonian of Eq. (5.5) to a molecule with 2n electrons and
and the explicit expression for the Hamiltonian. A simple extension of the helium Hamiltonian of Eq. (5.5) to a molecule with 2n electrons and  atomic nuclei (the
atomic nuclei (the  nucleus has charge
nucleus has charge  gives
gives
Just like the helium Hamiltonian, the molecular Hamiltonian 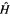 in Eq. (5.15) is composed (from left to right) of electron kinetic energy terms, nucleus-electron attraction potential energy terms, and electron–electron repulsion potential energy terms (cf. Fig. 5.1). This is actually the electronic Hamiltonian, since nucleus-nucleus repulsion potential energy terms have been omitted; from the Born–Oppenheimer approximation (section 2.3) these can simply be added to the electronic energy after this has been calculated, giving the total molecular energy for a molecule with “frozen nuclei” (calculation of the vibrational energy, the zero-point energy (ZPE), is discussed later). Calculation of the internuclear potential energy is trivial:
in Eq. (5.15) is composed (from left to right) of electron kinetic energy terms, nucleus-electron attraction potential energy terms, and electron–electron repulsion potential energy terms (cf. Fig. 5.1). This is actually the electronic Hamiltonian, since nucleus-nucleus repulsion potential energy terms have been omitted; from the Born–Oppenheimer approximation (section 2.3) these can simply be added to the electronic energy after this has been calculated, giving the total molecular energy for a molecule with “frozen nuclei” (calculation of the vibrational energy, the zero-point energy (ZPE), is discussed later). Calculation of the internuclear potential energy is trivial:
Substituting into Eq. (5.14) the Slater determinant and the molecular Hamiltonian gives, after much algebraic manipulation
for the electronic energy of a spatial orbitals  The terms
The terms
2n-electron molecule (the sums are over the n occupied in Eq. (5.17) have these meanings:
where

Ab initio calculations 169
The operator  is so called because it leads to
is so called because it leads to  the electronic energy of a single electron moving simply under the attraction of a nuclear “core”, with all the other electrons stripped away;
the electronic energy of a single electron moving simply under the attraction of a nuclear “core”, with all the other electrons stripped away;  is the electronic energy of, for example, H,
is the electronic energy of, for example, H, 
 or
or  (of course, it is different for these various species). Note that
(of course, it is different for these various species). Note that  (1) represents the kinetic energy of electron 1 plus the potential energy of attraction of that electron to each of the nuclei
(1) represents the kinetic energy of electron 1 plus the potential energy of attraction of that electron to each of the nuclei the 1 in parentheses in these equations is just a label showing that the same electron is being considered in
the 1 in parentheses in these equations is just a label showing that the same electron is being considered in
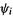 and
and  (we could have used, say, 2 instead). The integration in Eq. (5.18) is respect to spatial coordinates only,
(we could have used, say, 2 instead). The integration in Eq. (5.18) is respect to spatial coordinates only,  not
not  because spin coordinates have been “integrated out”: on integration, i.e. summation over the discrete spin variable, these give 0 or 1 [7,10,12]. We are left with the three integration variables (x, y, z) and so the integral is threefold.
because spin coordinates have been “integrated out”: on integration, i.e. summation over the discrete spin variable, these give 0 or 1 [7,10,12]. We are left with the three integration variables (x, y, z) and so the integral is threefold.
J is called a coulomb integral; it represents the electrostatic (i.e. coulombic) repulsion between an electron in  and one in
and one in  i.e. between the charge clouds of orbitals
i.e. between the charge clouds of orbitals  and
and  This may be clearer if one considers the integral as a sum of potential energy terms involving repulsion between infinitesimal volumeelements
This may be clearer if one considers the integral as a sum of potential energy terms involving repulsion between infinitesimal volumeelements 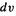 (Fig. 5.3). The 1 and 2 are just labels showing we are considering two electrons. The integrals J and
(Fig. 5.3). The 1 and 2 are just labels showing we are considering two electrons. The integrals J and
K allow each electron to experience the average electrostatic repulsion of a charge cloud due to all the other electrons. Since J represents potential energy corresponding to a destabilizing electrostatic repulsion, it is positive. As for  in Eq. (5.18), the integration is with respect to spatial coordinates because the spin coordinates have been integrated out. There are six integration variables, x, y, z for electron
in Eq. (5.18), the integration is with respect to spatial coordinates because the spin coordinates have been integrated out. There are six integration variables, x, y, z for electron  and x, y, z for electron
and x, y, z for electron  and so the integral is sixfold. Note that the ab initio coulomb
and so the integral is sixfold. Note that the ab initio coulomb

170 Computational Chemistry
integral J is not the same as what we called a coulomb integral in simple Hückel theory; that was  (Eq. (4.61)) and represents at least crudely the energy of an electron in the
(Eq. (4.61)) and represents at least crudely the energy of an electron in the  orbital
orbital  (section 4.3.4). The ab initio coulomb integral can also be written
(section 4.3.4). The ab initio coulomb integral can also be written
but unlike (5.20) this does not notationally emphasize the repulsion (invoked by the  operator) between electrons 1 and 2 (on the left and right, respectively, of
operator) between electrons 1 and 2 (on the left and right, respectively, of 
in Eq. (5.20)).
K is called an exchange integral; mathematically, it arises from Slater determinant expansion terms that differ only in exchange of electrons. Note that the terms on either side of  differ by exchange of electrons. It is often said to have no simple physical interpretation, but looking at Eq. (5.17), we can regard K as a kind of correction to J, reducing the effect of J (both J and K are positive, with K smaller), i.e. reducing the electrostatic potential energy due to the mutual
differ by exchange of electrons. It is often said to have no simple physical interpretation, but looking at Eq. (5.17), we can regard K as a kind of correction to J, reducing the effect of J (both J and K are positive, with K smaller), i.e. reducing the electrostatic potential energy due to the mutual 
 charge cloud repulsion referred to in connection with J. This reduction in repulsion arises because as particles with an antisymmetric wavefunction, two electrons cannot occupy the same spin orbital (roughly, cannot be at the same point in space), and can occupy the same spatial orbital only if they have opposite spins, so two electrons of the same spin avoid each other more assiduously than expected only from the coulombic repulsion taken into account by J. We could consider the summed 2J–K terms of Eq. (5.17) to be the true coulombic repulsion, corrected for electron spin, i.e. corrected for the Pauli exclusion principle effect. The J and K interactions are shown in Fig. 5.4 for a four-electron molecule,
charge cloud repulsion referred to in connection with J. This reduction in repulsion arises because as particles with an antisymmetric wavefunction, two electrons cannot occupy the same spin orbital (roughly, cannot be at the same point in space), and can occupy the same spatial orbital only if they have opposite spins, so two electrons of the same spin avoid each other more assiduously than expected only from the coulombic repulsion taken into account by J. We could consider the summed 2J–K terms of Eq. (5.17) to be the true coulombic repulsion, corrected for electron spin, i.e. corrected for the Pauli exclusion principle effect. The J and K interactions are shown in Fig. 5.4 for a four-electron molecule,
