4.2. Загальні принципи аналізу перехідних процесів

Математичний аналіз перехідних процесів в електричних колах базується на тому, що закони Кірхгофа слушні як до сталих, так і до несталих режимів. Використовуючи закони Кірхгофа для вузлових точок і замкнутих контурів, можна отримати для перехідного процесу лінійні диференціальні рівняння. За цими рівняннями визначають значення струмів і напруг в будь-який момент часу процесу. Значення постійних інтегрування знаходять з граничних умов, що визначаються законами комутації.

Для спрощення розв’язання диференційних рівнянь і полегшення їх аналізу перехідні процеси прийнято розглядати як результат накладання двох режимів – примусового і вільного. Відповідно з цим дійсний (фактичний) струм в колі і уявляється як сума двох складових: примусового струму і_пр, який встановлюється в колі після закінчення перехідного процесу, і вільного струму і_віл, що протікає в колі тільки під час перехідного процесу і = і_віл + і_пр.

Вільний струм поступово вщухає і при режимі, що встановився (t = ) стає рівним нулю. Тоді і| _{t = } = і_пр.

Оперуючи в розрахунках примусовою і вільною складовими, необхідно пам’ятати, що реально існуючими величинами є не окремі складові, а результуючі струми (або напруги).

4.3. Комутація напруги в rC-колі.

Приклад № 4.1.

Розглянемо просте коло, яке підключено до джерела постійної напруги U₀ (рис. 4.1).

а) б)

Рис. 4.1.

Нехай в початковому стані ключ К знаходиться в стані 2 (рис. 4.1-а). При цьому конденсатор не заряджений, u_C(0) = 0 і струм через опір r дорівнює нулю.

В момент часу t = 0 ключ К переводиться в стан 1, при якому до rC-кола підключається постійна напруга u(0) = U₀ і конденсатор починає заряджатись через опір r струмом i від джерела U₀. Коли напруга на конденсаторі дорівнюватиме напрузі U₀, процес заряду конденсатора закінчується і зарядний струм стане рівним нулю. Диференціальне рівняння, складене для утвореного при перемиканні ключа кола за другим законом Кірхгофа для t ≥ 0, має вид:

де добуток τ = r·C визначає закономірність зміни у часі напруги на конденсаторі.

Це диференціальне рівняння першого порядку, рішення якого звичайно знаходиться у виді u_C = А₂e^pt + А₁, де А₁, А₂ – деякі константи, які визначаються з початкових умов (при t = 0) і режиму, що встановиться (при t → ∞), а р – корінь характеристичного рівняння τр + 1 = 0, тобто p = –1/τ. При t → ∞ u_C(∞) = U₀, звідки А₁ = U₀. При t = 0 u_C(0) = 0 = А₂ + А₁ = А₂ + U₀, звідки А₂ = – U₀.

З урахуванням отриманих значень А₁ і А₂ рішення матиме вид:

.

Із складеного попередньо рівняння:

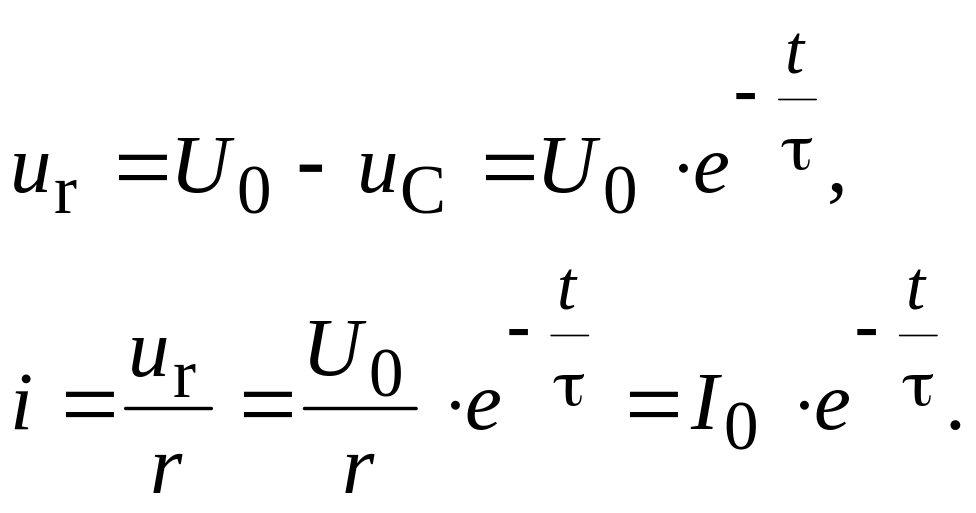
Величина τ = rC називається постійною часу rC-кола і характеризує швидкість протікання процесу заряду конденсатора. Вимірюється τ в секундах і співвідноситься із параметрами елементів кола так: 1 сек = 1Ом·1 Ф.

Значення струму і напруг при t = τ становитимуть:

u_C|_t = τ = 0,63·U₀; u_r|_t = τ = 0,37·U₀; i|_t = τ = 0,37·I₀,

при t = 2τ становитимуть:

u_C|_t = 2τ = 0,865·U₀; u_r|_t = 2τ = 0,135·U₀; i|_t = 2τ = 0,135·I₀,

при t = 3τ становитимуть:

u_C|_t = 3τ = 0,95·U₀; u_r|_t = 3τ = 0,05·U₀; i|_t = 3τ = 0,05·I₀.

Отже при t = 3τ напруга u_C відрізнятиметься від остаточного значення U₀ лише на 5%. Тому прийнято вважати, що при t ≥ 3τ перехідний процес заряду вже закінчився, а час t_п = 3τ прийнято вважати тривалістю перехідного процесу в rC-колі.

Визначається τ через величини r і C. При невідомих величинах r і C значення τ може бути визначено графічно, наприклад за осцилограмою перехідного процесу, як інтервал часу між моментом підключення U₀ і моментом, коли u_C дорівнюватиме 0,63·U₀.

П риклад № 4.2.

Вихідний стан – конденсатор повністю заряджений до величини U₀ і перехідні процеси заряду закінчені. Ключ К переводиться в положення 2 (рис. 4.2). Конденсатор почне розряджатись через резистор r. За деякий час перехідний процес розряду завершиться сталим режимом: u_C|_t = ∞ = 0; u_r|_t = ∞ = 0; i|_t = ∞ = 0.

За другим законом Кірхгофа при t ≥ 0 (де t = 0 – момент переводу ключа К в положення 2):

0 = u_r – u_C = ir – u_C¹,

де , і тоді рівняння за другим законом Кірхгофа можна записати у виді:

.

Враховуючи, що , остаточно матимемо:

Використовуючи загальне рішення звичайного диференціального рівняння першого порядку (див. приклад № 1), знаходимо постійні C₁ і C₂.

При t → ∞ u_C(∞) = 0, звідки А₁ = 0; при t = 0 u_C(0) = U₀ = А₂ + А₁, звідки А₂ = U₀, що дозволяє записати такі вирази для u_C, u_r, i:

Отримані вирази повністю описують процес розряду конденсатора. При t = 3τ напруга u_C|_{t = 3τ} = 5%·U₀, тому можна вважати, що при t ≥ 3τ перехідний процес розряду вже закінчився.

Важливим для практики є аналіз перехідних процесів в rC-колі при дії імпульсу прямокутної форми. при цьому суттєве значення має співвідношення тривалості імпульсу (t_і) і постійної часу кола (τ). На рис. 4.3-а показані графіки зміни напруг u_C і u_R при τ << t_і, а на рис. 4.3-б – графіки зміни цих напруг при τ >> t_і.

При аналізі вхідний імпульс прямокутної форми U_вх розглядається як сукупність двох стрибків напруг (U₁ і U₂), тобто U_вх = U₁ + U₂.

При τ << t_і конденсатор встигає повністю зарядитись за час t_і, але оскільки зарядний струм при цьому зменшується до нуля, то і напруга на опорі R (u_R) падає до нуля. в момент t₂ повністю заряджений до U₀ конденсатор розряджається через опір R, створюючи імпульс розряду від’ємної полярності.

При τ >> t_і конденсатор за час t_і встигає зарядитись лише до невеликої величини U_cm. На це ж значення зменшиться напруга u_R і стає в момент часу t₂ рівною (U₀ – U_cm). Після закінчення дії імпульсу конденсатор розряджається, створюючи на опорі імпульс від’ємної полярності, рівний –U_cm. по мірі розряду конденсатора u_С і u_R поступово зменшується до нуля.

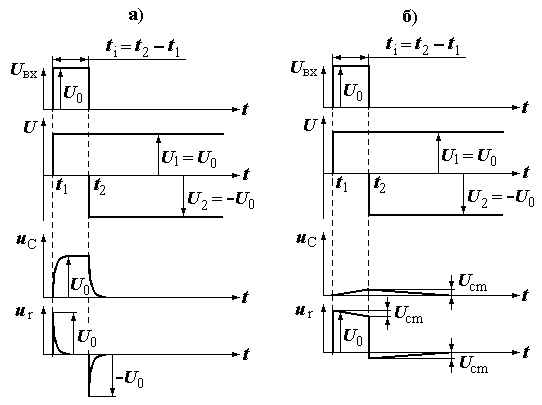
а) б)

Рис. 4.3.

Якщо подумки продиференціювати вхідний імпульс U_вх(t), вважаючи, що U_вх(t) не зростає і не спадає миттєво, то графік зміни u_r за формою нагадує похідну сигналу U_вх(t). Чим менше τ, тим більша ця схожість. Прийнято вважати, що для вхідного прямокутного імпульсу напруги тривалістю t_і напруга u_R пропорційна похідній вхідного сигналу, якщо τ ≤ 0,1·t_і, і таке rC-коло називається диференціюючим.

Якщо ж проаналізувати інтеграл вхідної напруги U_вх(t) за час t_і, то він уявляє собою лінійно зростаючу функцію, що за формою схожа на лінійно зростаючу напругу u_С у випадку τ >> t_і. Тому напругу на конденсаторі прийнято вважати пропорційною інтегралу вхідного прямокутного імпульсу, якщо τ ≥ 10·t_і, і таке коло називається інтегруючим.

Відзначимо, що диференціюючі кола в електронній техніці часто використовується як формувачі гострокінцевих імпульсів, а інтегруючі кола складають основу електронних схем для генерування напруг, що змінюються лінійно.