2.4.1. Комплексні числа. Форми представлення та основні операції.

• В алгебраїчній формі комплексне число с є сума дійсного числа a і уявного числа jb, тобто С = a + jb. Уявне число jb є добуток уявної одиниці 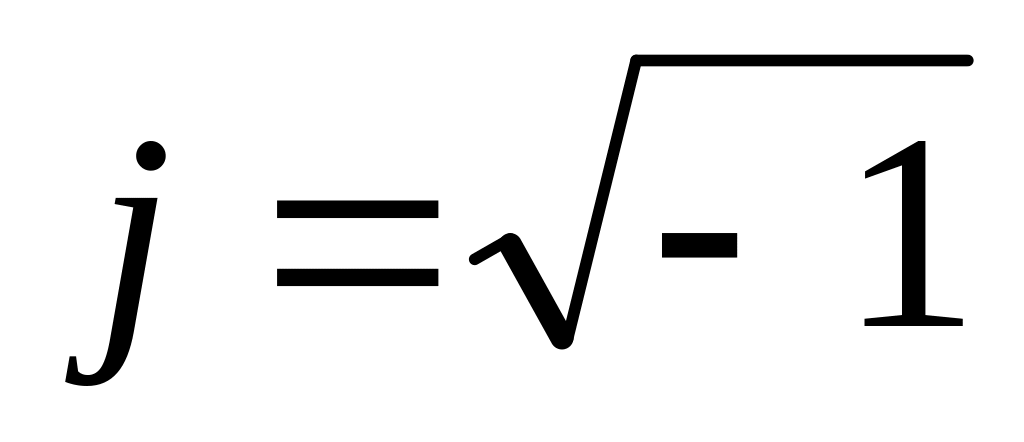і коефіцієнта при ній b.

Д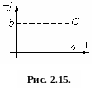 ля зображення комплексного числа с в графічній формі в прямокутній системі координат по горизонтальній осі відкладаються дійсна частина комплексного числа а, а по вертикальній осі – уявна частина jb. Комплексне число на такій комплексній площині зображується (рис. 2.15):

• точкою С з координатами (a; jb);

• вектором ОС, що починається в початку координат О, а закінчується в точці С з координатами (a; jb).

− Щоб записати комплексне число в показовій формі ¹ треба знати його модуль і аргумент. Модуль є довжина вектора ОС на комплексній площині:

.

а	b	чверть	
+	+	І	arctg b/a
–	+	ІІ	180 – arctg b/a
–	–	ІІІ	180 + arctg b/a
+	–	IV	– arctg b/a

Аргумент – це кут  між додатним напрямком дійсної осі і вектором ОС. Ясно, що b/a = tg , звідки  = arctg b/a.

При визначенні  треба мати на увазі, що обчислювальні засоби дають значення arctg b/a в межах 0   90. Тому отримане значення треба скорегувати згідно таблиці:

• Тригонометрична форма. При розв’язанні задач комплексним символічним методом виникає потреба перейти від показової форми до алгебраїчної. Вихідними є модуль і аргумент. Треба визначити дійсну і уявну частини і представити число в алгебраїчній формі.

З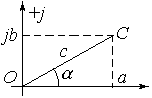 трикутника a = ccos , b = csin .

В комплексній формі С = a + jb = сcos  + jсsin  

Отриманий запис є тригонометричною формою комплексного числа.

Показова форма уявлення комплексного числа отримується із тригонометричної якщо неї підставити значення sin  і cos , які виражені через формули Ейлера:

.

Після перетворення і приведення подібних отримаємо остаточно С = cе ^j.

Для виконання арифметичних операцій додавання і віднімання над комплексними числами зручніше використовувати алгебраїчну форму: C₁  C₂ = a₁ + jb₁  a₂ + jb₂ = (a₁  a₂) + j(b₁  b₂)

Для операцій множення і ділення зручніше використовувати показову форму:

C₁  C₂ = с₁·e ^j  с₂·e ^j = с₁с₂·e ^{j( + )}; 

C₁ / C₂ = (с₁·e ^j) / (с₂·e ^j) = с₁ / с₂·e ^{j( – )} ,

але можна і алгебраїчну: C₁  C₂ = (a₁a₂ – b₁b₂) + j(a₁b₂ + b₁a₂);

.

Два комплексних числа називаються спряженими, якщо відрізняються тільки знаками уявної частини (в алгебраїчній формі), або знаками аргументів (в показовій формі), наприклад:

a + jb та a – jb;

с·e ^j  та с·e ^–j .

2.4.2. Уявлення параметрів електричного змінного струму через комплексні числа

Повертаючись до електричних величин можна провести аналогію між векторами, що обертаються і комплексними векторами. Ця аналогія дозволяє синусоїдальні величини відображувати комплексними числами. Комплексні значення струмів, напруг і ЕРС прийнято позначати .

Р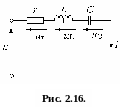 озглянемо сутність символічного методу на прикладі кола, що складається із послідовно з’єднаних елементів r, L, C і джерела змінної напруги u = U_m sin(ωt + ψ) (рис. 2.16). Таке коло описується рівнянням (за другим законом Кірхгофа):

u = u_r + u_L + u_C або .

Щоб розв’язати задачу визначення струму і прямо, необхідно розв’язати інтегродиференціальне рівняння. Для зазначеного кола це можливо, але в багатьох випадках це складно, а іноді і недосяжно.

В символічному методі замість гармонічної функції u = U_m sin(ωt + ψ) вводиться поняття комплексної гармонічної функції , яку можна уявити так: .

Величину називають комплексною амплітудою і позначають .

Тоді комплексну гармонічну функцію можна записати . Аналогічно записується для , . Іншими словами в символічному методі кожній гармонічній функції напруги u, струму і, ЕРС е ставиться у відповідність комплексна гармонічна функція . В подальшому гармонічні функції будемо називати оригіналами, а у комплексні гармонічні функції – зображеннями.

Застосуємо ці відповідності до компонентів рівняння послідовного кола.

Напруга на резисторі:

u_r = ri ~ , де .

Із останнього виразу видно, що відображення опору резистора в оригіналі співпадає із його відображенням в комплексі. Це означає, що r ~ r, тобто зображення і оригінал активного опору співпадають.

Напруга на індуктивності:

Тут , де X_L = jx_L.

В оригіналі стоїть оператор диференціювання гармонічної функції, а в зображенні – множення на постійний множник jω комплексної гармонічної функції. У індуктивності X_L = jx_L, тобто зображення і оригінал не співпадають.

Напруга на ємності:

Тут , де X_С = –jx_С.

При інтегруванні гармонічної функції операція інтегрування заміняється операцією ділення на величину jω комплексної гармонічної функції.

Наведені результати показують, що застосовуючи символічний метод розв’язання інтегродиференціальних рівнянь в оригіналі зводиться до рішення алгебраїчних рівнянь в зображеннях.

Покажемо це на прикладі інтегродиференціального рівняння послідовного кола (рис. 2.16):

Тут – повний комплексний опір. Його модуль дорівнює .

Закон Ома для послідовного кола у символічній формі можна записати у виді . Для середньоквадратичних значень закон Ома має вид або .

Отже, використовуючи символічний метод задача рішення інтегродиференціального рівняння звелася до рішення одного рівняння з одним невідомим за законом Ома.

Послідовність розрахунку виглядає так:

1. За значенням прикладеної напруги u = U_msin(ωt + ψ) знаходять її зображення .

2. Через параметри кола r, L, C визначають зображення відповідних опорів: r = r; X_L = jx_L = jωL; X_C = –jx_C  = –j·1/(ωC); Z = r + j(X_L – X_C).

3. За законом Ома знаходять 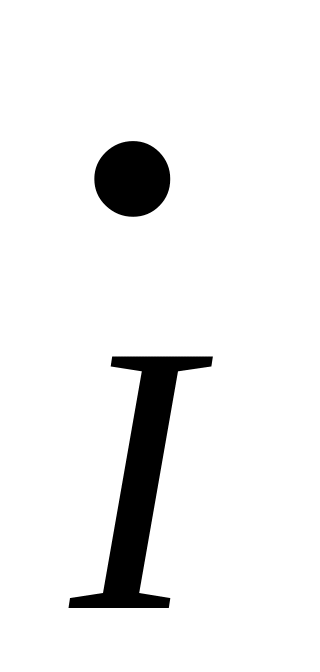або : 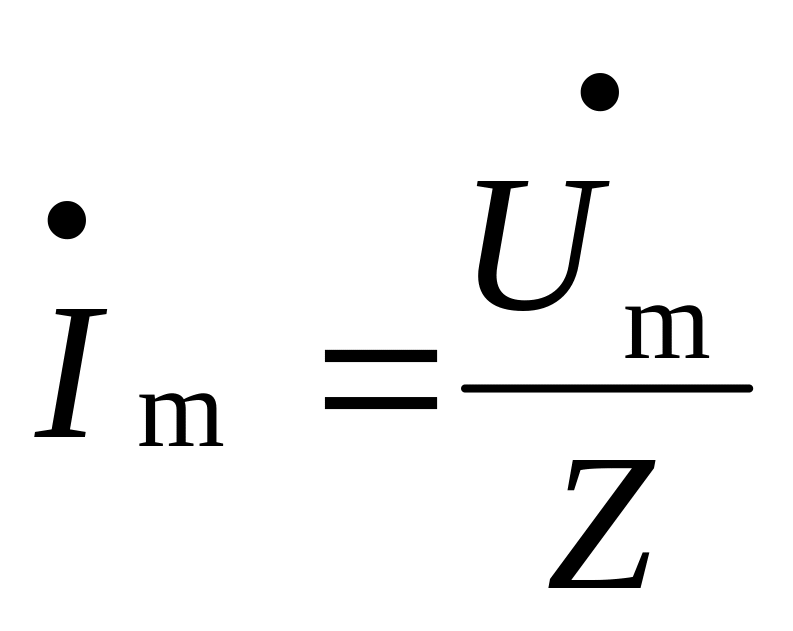; і отримують результат в символічному виді.

Тепер задача полягає в тому, щоб за зображенням знайти фактичний струм в колі. Для цього необхідно знайдений струм в колі записати у вигляді комплексної гармонічної функції у тригонометричній формі

і згадати якою функцією була представлена прикладена напруга. В цьому прикладі вона була представлена синусом.

При синусі: . Символом «Im» виокремлюють коефіцієнт уявної частини комплексного числа.

П ри косинусі: . Символом «Re» позначають коефіцієнт дійсної частини.

Згадаємо вже знайомі кола з активним опором, індуктивністю і ємністю (рис. 2.17).

Побудуємо для цих кіл векторні діаграми, але вже на комплексній площині, вважаючи, що розташування вектора величини з нульовою початковою фазою співпадає з дійсною додатною піввіссю.

В усіх випадках вектор напруги направлений по осі дійсних чисел. Тому комплекс напруги , де U – модуль комплексу напруги, а 0 – його початкова фаза.

Комплекс струму:

• у першому випадку –

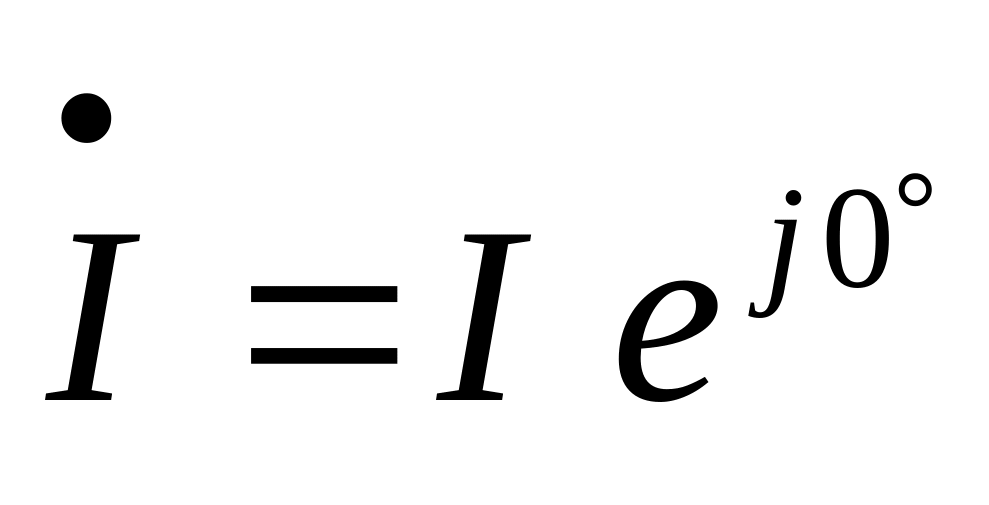
• у другому випадку –

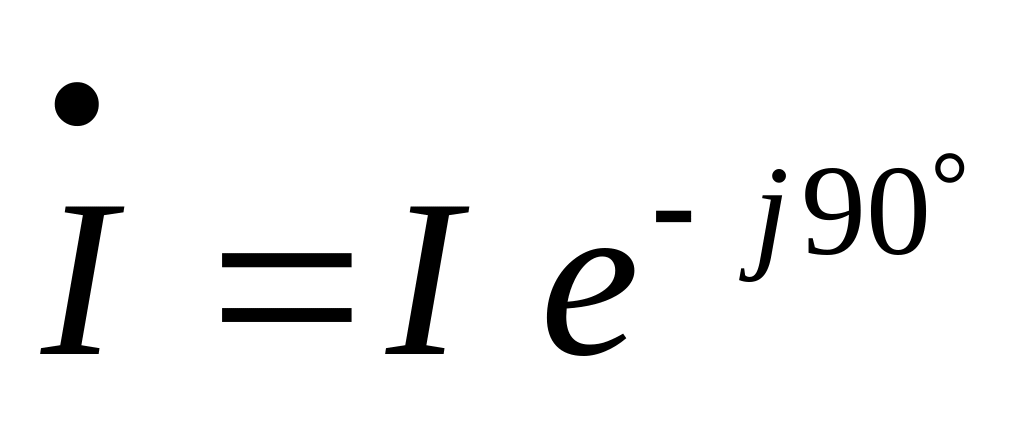
• у третьому випадку –

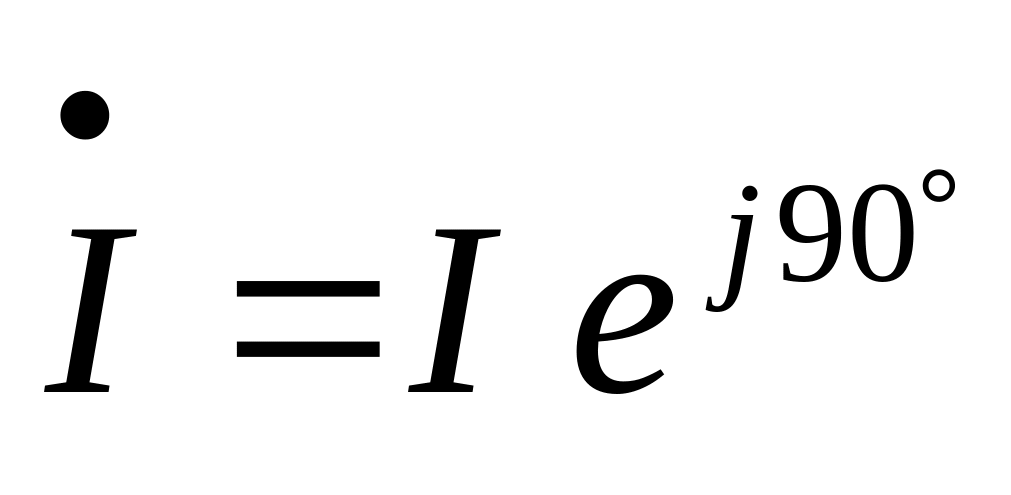
Отже комплексне зображення синусоїдальних величин визначає її діюче (амплітудне) значення і зсув фаз відносно вихідної величини, початкова фаза якої вважається рівною нулю.

Закони Кірхгофа. При розрахунку кіл синусоїдального змінного струму використовуються закони Кірхгофа, що справедливі для миттєвих, амплітудних та діючих значень, але:

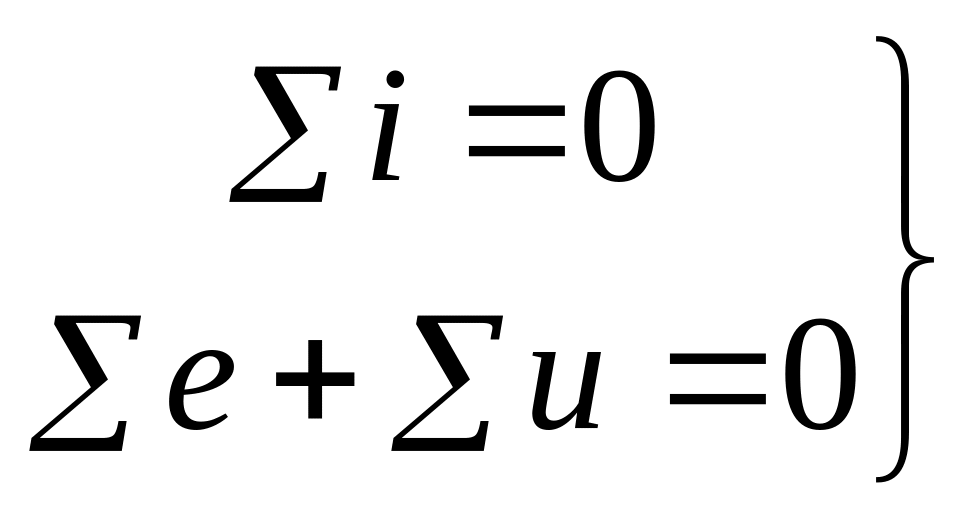для миттєвих значень – суми алгебраїчні.

ці рівняння справедливі у векторній формі, тобто суми не алгебраїчні, а векторні.