1.2.2. Перетворення трикутника опорів в еквівалентну зірку.

При розрахунку електричних кіл, які не вдається звести до одного результуючого опору шляхом заміни послідовно і паралельно з’єднаних опорів їх еквівалентними величинами доводиться вдаватись до більш складних перетворень. Зокрема, якщо в колі зустрічається замкнутий контур з трьох опорів R _AB, R _BC, R _CA, що утворюють сторони трикутника, то ці опори заміняють трьома опорами R _A, R _B, R _C, що з’єднані в одній вузловій точці О і утворюють трипроменеву зірку (  ).

При такому перетворенні опори між точками А і В, В і С та С і А (рис. 1.17) повинні бути однаковими в обох видах з’єднання:

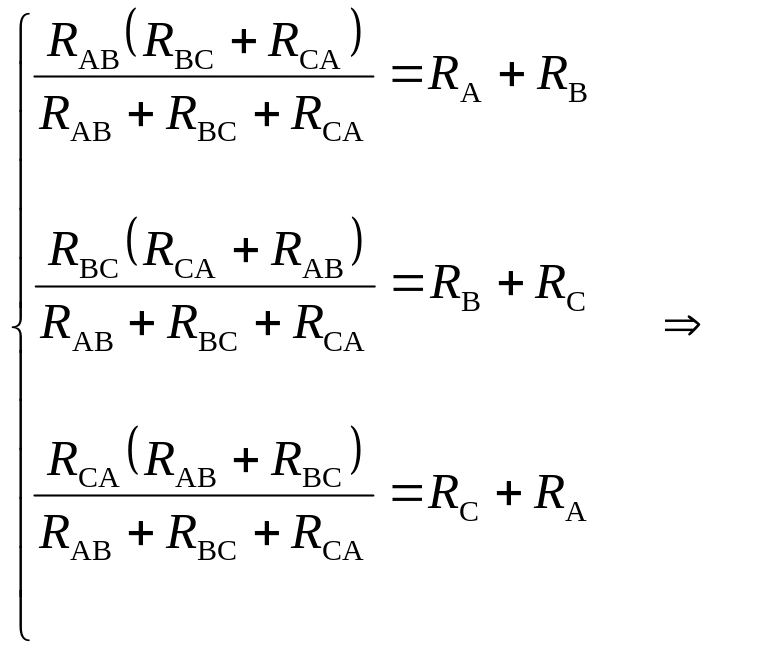
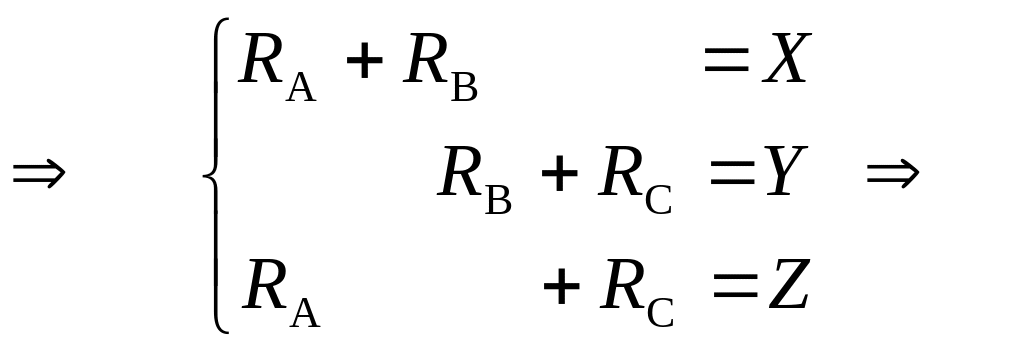
Тут використані правила визначення опорів при паралельному та послідовному з’єднані елементів електричних кіл. Тоді з цих рівнянь легко отримати:

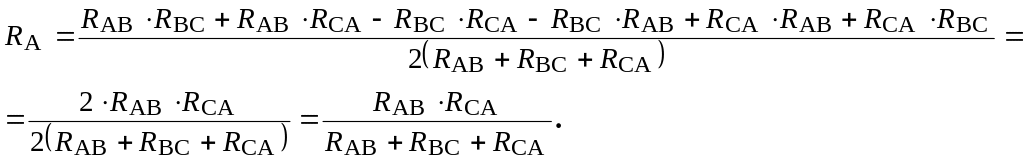
Аналогічно

При зворотному переході від зірки опорів до еквівалентного трикутника опорів () опори R _AB, R _BC, R _CA визначаються через опори R _A, R _B, R _C :

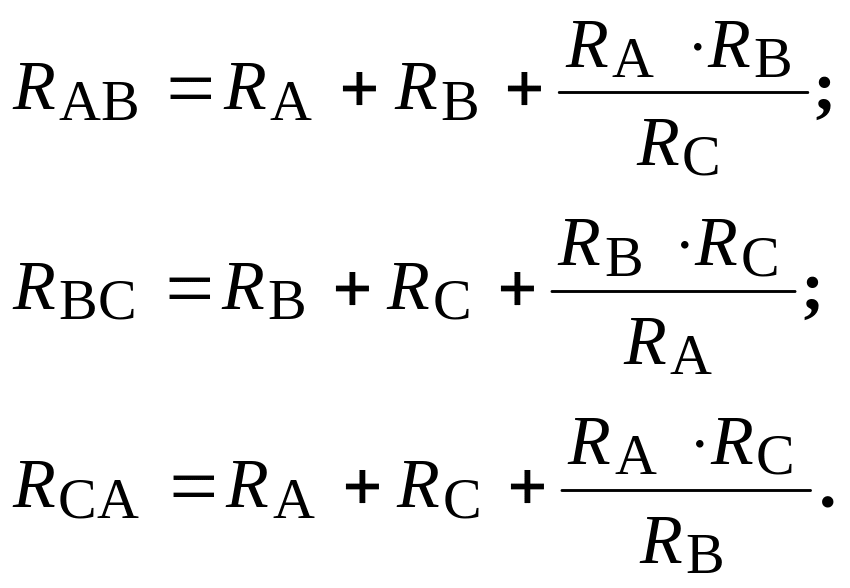
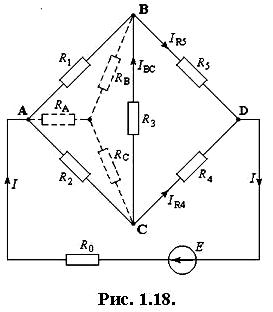
Використання наведених формул перетворення в розрахунках електричних кіл розглянемо на прикладі схеми електричного мосту (рис. 1.18).

Задача: визначити струм в перемичці ВС схеми.

Вихідні дані: Е = 32 В; R ₀ = 1 Ом; R ₁ = 10 Ом; R ₂ = 15 Ом; R ₃ = 25 Ом; R ₄ = 12,5 Ом; R ₅ = 25 Ом.

Розв’язання:

Замінимо трикутник опорів R ₁, R ₂, R ₃  еквівалентною зіркою з променями:

 

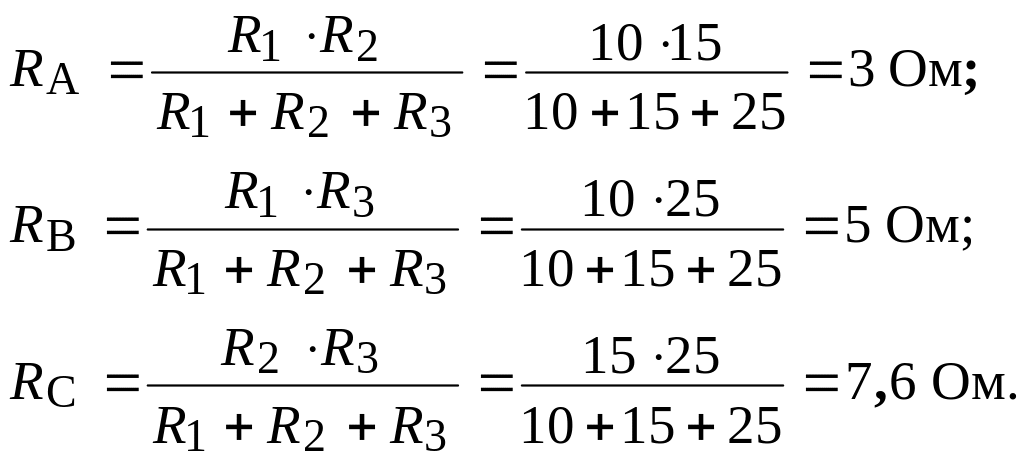
Загальний опір кола:

Струм в нерозгалуженій частині кола:

Позначимо струми в паралельних вітках із опорів R _B і R ₅ – I _R5 та із опорів R _C і R ₄ – I _R4. Тоді:

.

Ця формула походить з пропорції (струми в паралельних вітках зворотно пропорційні опорам віток) або .

З математики відома властивість пропорцій: якщо справедлива пропорція , то справедливий вираз , а в цьому випадку – .

Оскільки I _R4 + I _R5 = І, то .

Отже , а I _R4 = І – I _R5 = 2 – 0,8 = 1,2 А.

З рівняння, складеного за другим законом Кірхгофа (див. наступний підрозділ) для контуру BDCB – I _BCR ₃ + I _R5R ₅ – I _R4R ₄ = 0, маємо:

.

1.2.3. Закони Кірхгофа.

В попередніх параграфах були наведені приклади розрахунку простих кіл, де використовувався метод трансфігурації кола і закон Ома. Розрахувати складне коло таким чином не вдається або розрахунок пов’язаний із значним об’ємом обчислень. Тому у випадку розрахунку складного кола залучаються інші закони. Класичними законами для розрахунку складних кіл є закони Кірхгофа. Існують перший і другий закони (правила) Кірхгофа.

До струмів вузлів схеми застосовується перший закон Кірхгофа: сума струмів, що підходять до будь-якої точки розгалуження (вузла), дорівнює сумі струмів, що відходять від неї. Якщо струми, що підходять до точки, вважати додатними, а такі, що відходять від неї, – від’ємними, то перший закон Кірхгофа для кіл постійного струму можна сформулювати так: алгебраїчна сума струмів у вузлі дорівнює нулю (І = 0).

Цей закон випливає із закону збереження електричного заряду (алгебраїчна сума зарядів електрично замкнутої системи зберігається). Перший закон Кірхгофа є наслідком принципу неперервності електричного струму, відповідно до якого сумарний потік зарядів через будь-яку замкнену поверхню дорівнює нулю, тобто кількість зарядів, що виходять через цю поверхню має дорівнювати кількості зарядів, що входять. Підстава цього принципу очевидно, тому що при порушенні його електричні заряди всередині поверхні повинні були б або зникати, або виникати без видимих причин. Якщо заряди переміщаються всередині провідників, то вони утворюють в них електричний струм. Величина електричного струму може змінитися тільки у вузлі кола, оскільки зв’язки вважаються ідеальними провідниками. Тому, якщо оточити вузол довільною поверхнею, то потоки зарядів через цю поверхню будуть тотожні струмам в провідниках, що утворюють вузол, і сумарний струм у вузлі повинен бути рівним нулю.

Згідно другого закону Кірхгофа для кіл постійного струму, в усякому замкнутому контурі алгебраїчна сума падінь напруг на всіх опора, що включені в цей контур і алгебраїчна сума ЕРС в цьому контурі дорівнює нулю (ІR + Е = 0).

Другий закон Кірхгофа пов’язаний з поняттям потенціалу електричного поля, як роботи, що виконується при переміщенні одиничного точкового заряду в просторі. Якщо таке переміщення відбувається по замкнутому контуру, то сумарна робота при поверненні у вихідну точку дорівнюватиме нулю. В іншому випадку шляхом обходу контуру можна було б отримувати позитивну енергію, порушуючи закон її збереження.

Кожен вузол або точка електричного кола володіє власним потенціалом і, при переміщенні вздовж замкнутого контуру, здійснюється робота, яка при поверненні у вихідну точку дорівнюватиме нулю. Ця властивість потенційного електричного поля і описує другий закон Кірхгофа в застосуванні до електричного кола.

Я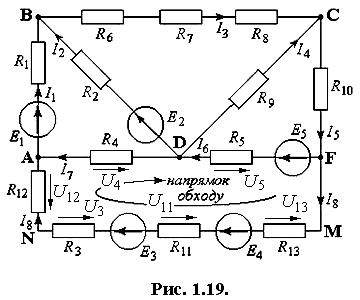 к приклад застосування законів Кірхгофа розглянемо схему, що наведена на рис. 1.19.

Вузли схеми: A, B, C, D, F.

Вітки: AB, BC, CD, BD, CF, AD, DF, ANMF.

Контури: ABDA, BCDB, CDFC, ADFMNA.

Перший закон Кірхгофа, наприклад, для вузла А визначається рівнянням: І ₇ + І ₈ – І ₁ = 0.

Другий закон Кірхгофа, наприклад, для контуру ADFMNA визначається рівнянням:

U₄ + U₅ – E₅ – U₁₃ + E₄ – U₁₁ + E₃ – U₃ – U₁₂ = 0, або

I₇R₄ + I₆R₅ − E₅ − I₈R₁₃ + E₄ − I₈R₁₁ + E₃ − I₈R₃ − I₈R₁₂ = 0, або

I₇R₄ + I₆R₅ − I₈(R₁₃ + R₁₁ + R₃ + R₁₂) = E₅ − E₄ − E₃.