2 .3.5. Паралельне з’єднання елементів r, l, c на синусоїдальному змінному струмі.

На рис. 2.10 показана схема паралельного з’єднання елементів із проставленими на них струмами і напругами.

Рівняння схеми − . Йому відповідає векторна діаграма на рис. 2.11-а.

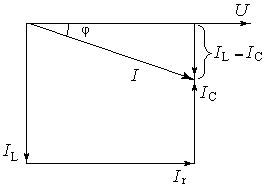
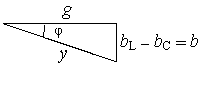
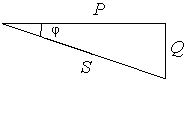
а) б) в)

Рис. 2.11.

Використавши до рис. 2.11-а аналогічні попередньому випадку міркування, отримаємо трикутник провідностей (рис. 2.11-б) і потужностей (рис. 2.11-в), із яких знайдемо:

.

Вирази для трикутника потужностей отримаємо, якщо всі величини трикутника провідностей помножимо на U² (рис. 2.11-в):

2.3.6. Еквівалентний перехід від послідовної схеми до паралельної.

На рис. 2.12 показані дві схеми з’єднання елементів r, L, C – послідовна (рис. 2.12-а) і паралельна (рис. 2.12-б).

а) б)

Рис. 2.12.

На схемах x = x_L –x_C, а b = b_L – b_C.

Під еквівалентністю обох схем розуміють рівноцінність заміни однієї схеми іншою – без порушення схемами із боку входу струмів, напруг і фазових співвідношень (згадайте еквівалентне перетворення трикутника опорів в еквівалентну зірку п. 1.2.2).

Математично це можна записати так:

z₁ = z₂ = z; φ₁ = φ₂ = φ.

Схемам рис. 2.12 властиві залежності:

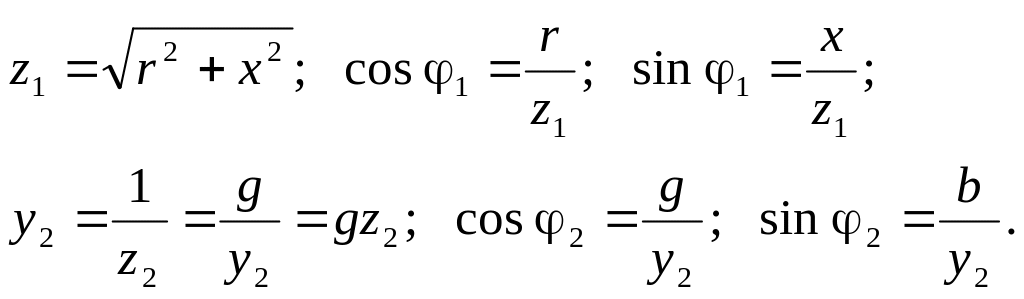
При еквівалентності схем z₁ = z₂ = z, а φ₁ = φ₂ = φ, маємо:

Отже, знаючи параметри послідовної схеми можна знайти параметри еквівалентної паралельної, і зворотно.

2.3.7. Змішане з’єднання елементів r, l, c на синусоїдальному змінному струмі.

На рис. 2.13 показано схема із змішаним з’єднанням елементів. Кожна із віток є послідовним з’єднанням, а між собою вітки з’єднані паралельно.

Аналіз змішаного з’єднання краще проводити, якщо скористатись перетворенням послідовних віток в еквівалентні паралельні. На рис. 2.14 показана перетворена паралельна схема. Параметри схеми отримані за формулами із попереднього п. 2.3.6.

Запишемо для схеми на рис. 2.14 очевидні співвідношення:

Параметри схеми рис. 2.14 знаходяться за формулами еквівалентного переходу від послідовного кола до паралельного:

Струми схеми дорівнюють:

Повна провідність кола визначається за виразом:

Остання формула знадобиться в подальшому при дослідженні резонансу в змішаному колі.

Беручи за базовий вектор U, як спільний для всіх елементів, знайдемо струми і побудуємо загальну векторну діаграму кола. Вона наведена на рис. 2.14-а.

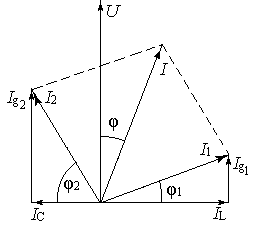
а) б)

Рис. 2.14.

Без застосування еквівалентного перетворення змішаної схеми в чисто паралельну побудувати подібну векторну діаграму було б менш наочно, хоча і можливо. Для цього необхідно знайти повні опори кожної із паралельних віток:

,

обчислити кути φ₁ і φ₂ за формулами:

і знайти струми І₁ і І₂.

На рис. 2.14-б показана векторна діаграма струмів І₁, І₂ і напруг U, U_r1, U_r2, U_L, U_C.

2.4. Символічний метод розрахунку кіл синусоїдального струму.

Вже можна передбачити, що при розрахунках кіл змінного струму треба буде використовувати складні перетворення з величинами, до яких входять тригонометричні функції, або виконувати графічні побудови із векторами.

Ефективний метод розрахунку кіл змінного струму є символічний метод, оснований на зображенні електричних величин (струм, напруга, ЕРС, опори, провідності, потужності) комплексними числами. В цьому випадку для розрахунку кіл змінного струму можна використовувати закони Кірхгофа і всі методи розрахунку складних кіл постійного струму.