1.7.2. Помехи

Наряду с полезными сигналами на вход измерительного прибора действуют помехи. Помехи – это посторонние электрические возмущения, накладывающиеся на передаваемый сигнал и затрудняю­щие его прием. По типу взаимодействия с сигналом помехи делятся на ад­дитивные и мультипликативные. Для случая аддитивной помехи сигнал x(t) на входе приемного устройства запишется как

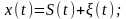(1.7.6)

для мультипликативной –

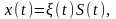(1.7.7)

где S(t) – полезный сигнал; 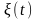– помеха.

Мультипликативные помехи проявляются как замирание сигнала. Они обусловлены изменением коэффициента передачи линии связи, что обусловлено резкими не­периодическими ухудшениями пара­метров линии связи. Помехи этого вида приводят к появлению груп­повых ошибок.

Источниками помех являются внешние воздействия (искрообразование в электрических цепях в процессе их коммутации, различ­ные наводки и т.д.) и внутренние воздействия (тепловой шум).

В зависимости от характера источника помехи могут носить импульсный или флуктуационный характер.

Импульсные помехи – это последовательность импульсов случайной ам­плитуды, длительности и со случайным моментом появления отдельных импульсов. Импульсные помехи следуют друг за другом относительно редко, и для них характерно отсутствие наложений в приемном устройстве измерительного прибора переходных процессов от отдельных импульсов помех. Простейшие импульсные помехи показаны на рис. 1.7.1.

Рис. 1.7.1. Импульсная помеха

Апериодическая помеха, которая выражается уравнением показательной функции

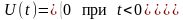(1.7.8)

и полупериодическая помеха (имеет форму затухающего колебания)

(1.7.9)

Флуктуационные помехи представляют собой непрерывную случайную функцию времени. В случае большого числа взаимных наложений реакций входной части измерительного устройства на приходящие на его вход импульсы на выходе его будет непрерывный случайный про­цесс, т.е. флуктуационная помеха. Флуктуационные помехи имеют вид непрерывного случайно изменяющегося колебания.

Важными характеристиками этих помех являются мощность помех, закон распределения амплитуд и вид энергетического спектра (функция корреляции).

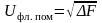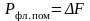Один и тот же источник помех может создавать импульсные и в то же время флуктуационные помехи в узкополосном приемной части измерительного устройства. При равномерном по частоте спектре помех в линии связи эффективное напряжение флуктуационных помех на выходе приемного устройства пропорционально квадратному корню полосы пропускания, т.е. , а мощность . При импульс­ных помехах амплитуда и мощность помехи пропорциональны полосе пропускания.

Способы борьбы с помехами зависят от их спектра. По относительно­му спектральному составу различают следующие три вида помех:

– высокочастотные помехи с периодом повторения Т_п, значительно меньшим времени измерения Т_изм;

– высокочастотные помехи с периодом повторения, близким к Т_изм, – периодическая помеха;

– низкочастотные помехи с периодом повторения Т_п, значительно превышающим Т_изм.

Высокочастотную составляющую уменьшают осреднением, если при этом обеспечивается необходимое быстродействие данного средства из­мерения.

Периодическая помеха является следствием различных наводок с ча­стотой сети переменного тока. Их уменьшают, применяя фильтры, интег­рирование за время, кратное периоду помехи, и осуществляя синфазиро-вание моментов измерения и перехода помехи через нулевое значение.

Низкочастотная составляющая устраняется обычными способами, разработанными для систематических погрешностей.