
- •200106 «Информационно-измерительная техника и технологии»
- •Введение
- •1.2. Сигналы
- •1.3. Преобразование измерительных сигналов
- •1.4. Спектр периодических сигналов
- •1.5. Модуляция
- •1.5.1. Амплитудная модуляция
- •1.5.2. Частотная модуляция
- •1.5.3. Фазовая модуляция
- •1.5.4. Двукратные виды модуляции
- •1.6. Квантование
- •1.6.1. Квантование по уровню
- •1.6.2. Квантование по времени
- •1.6.3. Квантование по уровню и времени
- •1.7. Кодирование
- •1.7.1. Цифровые коды
- •1.7.2. Помехи
- •1.8. Модель канала
- •Раздел 2 измерительные каналы и их разделение
- •2.1. Канал связи и его характеристики
- •2.2. Согласование канала с источником информации
- •2.3. Линии связи для передачи измерительной информации
- •2.4. Структуры линий связи
- •2.5. Многоканальные системы для передачи измерительной информации
- •2.6. Погрешность систем с частотным разделением каналов
- •2.7. Погрешности систем с временным разделением каналов
- •Раздел 3 принципы обработки данных
- •3.1. Виды погрешностей
- •3.2. Обработка результатов измерений. Оценки измеряемой величины
- •3.3. Обработка результатов прямых равноточных измерений
- •3.4. Обработка результатов косвенных измерений
- •3.5. Обработка результатов совместных измерений
- •3.6. Обработка результатов неравноточных измерений
- •3.7. Проверка статистических гипотез
- •3.7.1. Проверка соответствия гипотезы и экспериментальных данных
- •3.7.2. Исключение резко отклоняющихся значений
- •3.8. Построение эмпирических распределений
- •3.9. Критерии согласия
- •3.9.1. Критерий согласия Пирсона
- •3.9.2. Критерий согласия Колмогорова
- •Раздел 4 планирование многофакторного эксперимента
- •4.1. Задачи планирования эксперимента
- •4.2. Пассивные эксперименты
- •4.3. Дисперсионный анализ
- •4.4. Регрессионный анализ
- •4.5. Активный эксперимент
- •4.6. Полный факторный эксперимент
- •4.7. Дробный факторный эксперимент
- •4.8. Устранение влияния временного дрейфа
- •4.9. Проведение факторного эксперимента и обработка его результатов
- •4.10. Оптимизация
- •4.11. Рандомизация
- •Раздел 5 введение в алгоритмическую теорию измерений
- •5.1. Вводные замечания
- •5.2. Развитие понятий числа и измерения величин
- •5.3. Теория шкал и алгоритмические измерения
- •5.4. Алгоритмы измерения в номинальной шкале, аддитивной и порядка
- •5.5. Моделирование цифровых алгоритмических измерений
- •5.6. Эквивалентность между фильтрацией и алгоритмическим измерением
- •5.7. Моделирование сигналов. Дискретизация
- •5.7.1. Модели дискретизации аналогового сигнала
- •5.7.2. Дискретизация с усреднением
- •5.7.3. Дискретизация сигналов конечной длительности
- •5.8. Цифровое представление информации
- •5.9. Системы счисления с иррациональными основаниями
- •5.9.1. Золотая пропорция
- •5.9.2. Числа Фибоначчи
- •5.9.4. Код золотой p-пропорции
- •5.10. Общий алгоритм метрологического кодирования
- •5.10.1. Алгоритм Стахова
- •5.10.2.Фибоначчиевы алгоритмы цифрового метрологического кодирования
- •Раздел 6 введение в информационную теорию измерений
- •6.1. Основные положения теории информации
- •6.1.1. Энтропия
- •6.1.2. Единицы измерения энтропии
- •6.1.3. Условная энтропия (энтропия помехи)
- •6.1.4. Суммирование нескольких погрешностей
- •6.1.5. Явление «краевой эффект». Приближенность информационных оценок каналов передачи информации
- •6.1.6. Основные положения теории информации для характеристики процесса измерения
- •6.2. Сущность измерения
- •6.2.1. Понятие натурального ряда однородных величин
- •6.2.2. Понятие шкалы реперов измеряемой величины
- •6.2.3. Измерение как сужение интервала неопределенности
- •6.3. Измерительные преобразования, функциональные шкалы, единицы измеряемой величины
- •6.3.1. Функциональная шкала измеряемой величины
- •6.3.2. Понятие единицы измерения
- •6.3.3. Метод построения измерительных устройств
- •6.4. Измерительные преобразования и преобразователи
- •6.5. Энтропийное значение погрешности
- •6.5.1. Математическое определение энтропийного значения погрешности
- •6.5.2. Эффективное значение погрешности
- •6.6. Сравнение энтропийного и среднеквадратического значений погрешности для плавных симметричных одномодальных законов распределения погрешностей
- •6.7. Энтропийное значение погрешности – основной критерий точности приборов и измерений
- •6.8. Определение энтропийного значения погрешности на практике
- •6.9. Суммирование погрешностей измерительных устройств
- •6.10. Статистическое суммирование погрешностей при наличии корреляции
- •6.11. Энтропийное значение результирующей погрешности
- •6.12. Суммирование погрешностей с равномерными законами распределения вероятностей
- •6.13. Суммирование погрешностей при равномерном и нормальном законах распределения составляющих результирующей погрешности
- •6.14. Суммирование погрешностей при произвольной степени корреляции и произвольных законах распределения вероятностей составляющих результирующей погрешности
- •И объемов (n) выборок
- •Интервала
- •Оглавление
6.1.4. Суммирование нескольких погрешностей
Рассматривая энтропию непрерывных случайных функций можно сказать, что максимальная энтропия при заданной средней мощности (т.е. при данном значении ) имеет шум или погрешность с нормальным распределением. Исходя из этого, для характеристики помех с законом распределения, отличным от нормального, используется энергетически информационное понятие энтропийной мощности. Она определяется как мощность шума с нормальным распределением, имеющим то же самое значение энтропии, что и данный шум с произвольным законом распределения.
Располагая понятиями полной и энтропийной мощности помехи или погрешности, в 15-й теореме формулируется основное соотношение, характерное для случая суммирования ряда случайных погрешностей с различными законами распределения.
Из теории вероятностей
известно, что при суммировании нескольких
независимых случайных величин с
дисперсиями
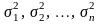 дисперсия их суммы равна сумме дисперсий,
т.е.
дисперсия их суммы равна сумме дисперсий,
т.е.
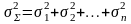 . (6.1.7)
. (6.1.7)
Однако форма закона распределения при суммировании случайных величин сохраняется лишь для небольшого числа законов распределения (например, нормального, закона Пуассона и некоторых других). В общем же случае при суммировании случайных величин законы их распределения деформируются и закон распределения суммы оказывается отличным от закона распределения слагаемых. Так, например, при суммировании двух погрешностей с равномерными законами распределения закон распределения суммы является трапецеидальным или даже треугольным. А так как энтропия зависит именно от формы закона распределения (в то время как дисперсия суммы равна сумме дисперсий независимо от формы закона распределения), то соотношения между дисперсией и энтропией могут оказаться достаточно разнообразными. Задача о поиске этого соотношения и указания на некоторые его ограничения формулируются в виде 15-й теоремы.
Теорема 15.
Пусть средние
мощности двух ансамблей равны
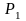 и
и
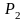 ,
а их энтропийные
мощности пусть равны
,
а их энтропийные
мощности пусть равны
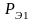 и
и
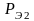 .
Тогда энтропийная мощность суммы
.
Тогда энтропийная мощность суммы
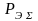 ограничена неравенствами
+
≥
≥
+
.
ограничена неравенствами
+
≥
≥
+
.
Теорема 15 утверждает, что энтропийная мощность суммы случайных погрешностей не меньше суммы их энтропийных мощностей и не больше суммы полных мощностей, а, следовательно, не может быть найдена ни путем суммирования энтропийных мощностей, ни путем суммирования полных мощностей. Таким образом, 15-я теорема Шеннона является не решением, а лишь постановкой задачи точного суммирования случайных погрешностей.
6.1.5. Явление «краевой эффект». Приближенность информационных оценок каналов передачи информации
Вопрос об учете явления «краевого эффекта» рассматривается при доказательстве 11-й и 17-й теорем. Сущность «краевого эффекта» состоит в следующем. Пусть по каналу передачи информации передается случайная величина X, которая может принимать ряд значений в пределах от X = Х1 до X = Х2.
В
результате измерения получаем показание
прибора, например, в виде точки Хп.
Из-за случайной погрешности прибора
этому показанию с теми или иными
вероятностями может соответствовать
целый ряд действительных значений X.
Не
учитывая маловероятных случаев, такую
ситуацию можно изобразить веером лучей,
сходящихся в точке Хп.
Неопределенность,
вносимая в результат измерения этим
веером, обусловленным случайной
погрешностью прибора, и описывается
условной энтропией
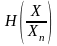 ,
т.е. энтропией действительных значений
X
при
известном значении Хп.
Но
наличие случайной погрешности прибора
создает и другое явление. При передаче
по каналу крайних значений Х1
и
Х2
передаваемой
величины X
полученные
показания прибора могут быть и за
границами Х1
и
Х2.
Поэтому распределение различных значений
Хп
будет
шире распределения X.
,
т.е. энтропией действительных значений
X
при
известном значении Хп.
Но
наличие случайной погрешности прибора
создает и другое явление. При передаче
по каналу крайних значений Х1
и
Х2
передаваемой
величины X
полученные
показания прибора могут быть и за
границами Х1
и
Х2.
Поэтому распределение различных значений
Хп
будет
шире распределения X.
Точное определение
этого «расширенного» распределения и
его энтропии пока точно не известно,
однако можно установить возможные
пределы результата. Считая как вносимую
погрешность, так и измеряемую величину
X
независимыми
случайными величинами, для их суммирования
между собой можно использовать 15-ю
теорему. В любом частном случае
результирующий закон распределения
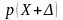 может быть найден как свертка заданных
законов распределения
может быть найден как свертка заданных
законов распределения
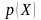 и
и
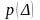 ,
а затем может быть вычислено значение
его энтропии и энтропийной мощности.
,
а затем может быть вычислено значение
его энтропии и энтропийной мощности.
Вследствие сложности
подобного точного решения, теоремы 17,
18, 19, 22 и 23 посвящаются поиску приближенных
решений проблемы «краевого эффекта» и
дают ряд рекомендаций. В теореме 17 он
показывает, что число различимых градаций
полученного результата Хп
может быть
оценено приближенно не по энтропийной
мощности, а по соотношению полных
мощностей сигнала Рх
и шума Рш.
Если считать,
что полная ширина разброса значений Хп
(от Хп
max
до Хп
min)
пропорциональна
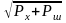 ,
а ширина веера лучей вокруг данного
значения X
соответственно
пропорциональна
,
а ширина веера лучей вокруг данного
значения X
соответственно
пропорциональна
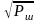 ,
то число различимых градаций Хп
равно
,
то число различимых градаций Хп
равно
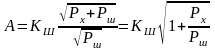 , (6.1.8)
, (6.1.8)
где
 – коэффициент Шеннона. Этот коэффициент
должен быть порядка единицы. Если
полагать
= 1, то
количество информации, получаемое при
данной мощности
– коэффициент Шеннона. Этот коэффициент
должен быть порядка единицы. Если
полагать
= 1, то
количество информации, получаемое при
данной мощности
 сигнала и
мощности
шума, равно
логарифму числа А
различимых
градаций, т.е.
сигнала и
мощности
шума, равно
логарифму числа А
различимых
градаций, т.е.
 (6.1.9)
(6.1.9)
Грубость
приближения состоит в том, что оба его
члена выражаются не через понятия
энтропии и энтропийной мощности, а через
полные мощности. Таким образом, приближение
заключается в том, что точное выражение
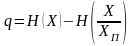 заменяется
выражением
заменяется
выражением
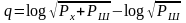 ,
где
,
где
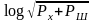 не равен
,
a
не равен
,
a
 не
равен
не
равен
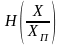 .
Поэтому
в теоремах 18, 19, 22 и 23 Шеннон рассматривает
ряд дальнейших приближений. В 18-й теореме
он показывает, что лучшими приближениями
вместо дроби
.
Поэтому
в теоремах 18, 19, 22 и 23 Шеннон рассматривает
ряд дальнейших приближений. В 18-й теореме
он показывает, что лучшими приближениями
вместо дроби
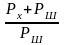 являются соотношения
являются соотношения
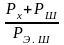 и
и
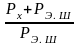 где
где
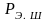 – значение энтропийной мощности шума.
Теорема 19 рекомендует в знаменателе
этой дроби всегда использовать
,
а в числителе
заменять на
– значение энтропийной мощности шума.
Теорема 19 рекомендует в знаменателе
этой дроби всегда использовать
,
а в числителе
заменять на
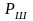 при
>
.
В
22 и 23 теоремах он приходит к заключению,
что если под
понимать
допустимую дисперсию ошибки передачи,
то рассматриваемую дробь лучше писать
в виде
при
>
.
В
22 и 23 теоремах он приходит к заключению,
что если под
понимать
допустимую дисперсию ошибки передачи,
то рассматриваемую дробь лучше писать
в виде
 вместо
вместо
 ,
где
,
где
 – энтропийная мощность сигнала, а
– его полная мощность.
– энтропийная мощность сигнала, а
– его полная мощность.
Таким образом, от различных приближенных методов учета «краевого эффекта» в виде соотношений: , или , Шеннон приходит к выражению , т.е. вообще к отказу от использования поправки на «краевой эффект», однако с заменой полных мощностей сигнала и шума их энтропийными значениями. Это существенное обстоятельство. Упрощение в виде замены энтропии или энтропийной мощности значением средней мощности или дисперсии равносильно отказу от энтропийного подхода. Это просто возврат к обычным методам теории вероятности и отказ от основного рационального зерна теории информации. Однако пренебрежение «краевым эффектом» при >> вполне правомерно и весьма упрощает математические преобразования, и, наоборот, сохранение под знаком логарифма вместо отношения суммы резко усложняет их, так как логарифм суммы не раскрывается, и дальнейшие преобразования становятся затруднительными.
