5.9. Системы счисления с иррациональными основаниями

Одним из интересных и перспективных направлений разви­тия цифровой техники для алгоритмических измерений является использование для цифровой обработки систем счисления с иррациональным основанием. К этому направлению относят также коды Фибоначчи. Рассмотрим основные теоретические положения, лежащие в основе построения упомянутых систем счисления.

В последние десятилетия числа Фибоначчи и золотую пропорцию стали использовать в теории кодирования информации. Наметились следующие направления: 1) избы­точные самосинхронизирующиеся коды Фибоначчи; 2) система счисления с иррациональным основанием типа золотой пропорции; 3) теория измерения на основе избыточных измерительных кодов; 4) фибоначчиевы системы счисления.

В перечисленных направлениях числа Фибоначчи и золотая пропорция выступают в роли фундаментального начала указан­ных выше направлений в теории измерения и кодирования, затрагивающих основы цифровой техники. За счет заложенной в них избыточности коды с иррациональными основаниями позволяют решить ряд задач, связанных с контролем измери­тельных и арифметических преобразований информации в циф­ровых системах.

5.9.1. Золотая пропорция

Рассмотрим следующую геометрическую задачу. На отрезке АВ требуется найти такую точку С на рис. 5.9.1, чтобы

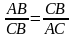. (5.9.1)

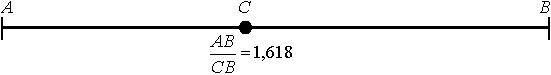
Рис. 5.9.1. Золотое сечение

Обозначим это отношение через х. Так как АВ = АС + СВ, то 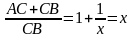, откуда следует уравнение для нахождения искомого отношения:

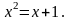(5.9.2)

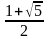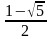Уравнение (5.9.2) имеет два корня: и . Положительный корень этого уравнения называют золотой пропорцией, а деление отрезка АВ в отношении (5.9.1) – золотым сечением. Золотая пропорция обладает следующими фундамен­тальными свойствами:

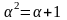; (5.9.3)

, (5.9.4)

где п – целое число.

Рассмотрим геометрическую прогрессию, образованную сте­пенями «золотой» пропорции, т.е.

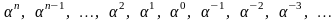(5.9.5)

Имея в виду (5.9.4), видим, что прогрессия (5.9.5) обладает тем свойством, что каждый член равен сумме двух по­следующих.

Задача о золотом сечении допускает следующее обобщение. Зададимся целым неотрицательным числом р и разделим отрезок АВ точкой С на две неравные части в такой пропорции, чтобы отношение большей части к меньшей СВ/АС равнялось p-й степени отношения всего отрезка к большей части его (рис. 5.9.2), т.е.

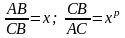. (5.9.6)

Так как АВ = АС + СВ, то 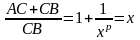, откуда следует искомое отношение:

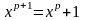(5.9.7)

Обозначим через α положительный корень уравнения (5.9.7). Это уравнение задает бесконечное число пропорциональных делений отрезка типа (5.9.6), так как каждому р соответствует свой вариант деления. Рассмотрим частные случаи.

При р = 0 деление отрезка (5.9.6) задается с помощью следующих соотношений: 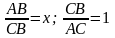, что соответст­вует классической дихотомии, т.е. α₀ = 2.

При р = 1 деление отрезка (5.9.6) сводится к "золотому" сечению, так как , а положительный корень уравнения (5.9.7) совпадает с «золотой» пропорцией, т.е. .

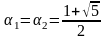С учетом этого обстоятельства положительный корень уравнения (5.9.7) назван золотой р-пропорцией.

На рис. 5.9.2 приведены приближенные значения золотой р-пропорции, соответствующие начальным значениям р.

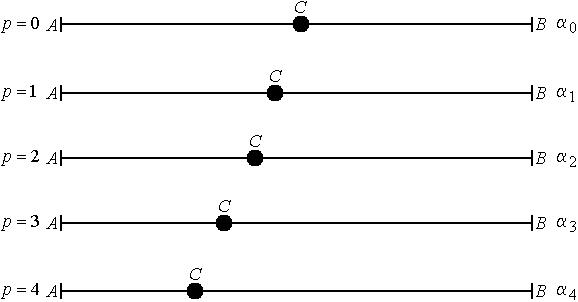
Рис. 5.9.2. Золотое p-сечение:

; ; ; ;

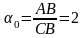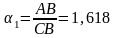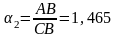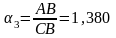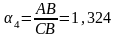
Из (5.9.7) следует фундаментальное свойство золотой р-про­порции, справедливое для любого целого п.

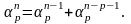(5.9.8)

Заметим, что это уравнение задает отношение эквивалент­ности, т.е. отношение подобия золотой р-пропорции. Индекс р определяет число классов эквивалентности; внутри каждого класса эквивалентности имеем п подобных корней.