4.6. Полный факторный эксперимент

Метод полного факторного эксперимента дает возможность получить математическое описание исследуемого процесса в некоторой локальной области факторного пространства, лежащей в окрестности выбранной точки с координатами .

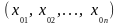Рассмотрим планирование факторного эксперимента на примере линейной полиномиальной математической модели, которая используется наиболее часто. В этом случае достаточно использовать только два уровня факторов.

Если число факторов известно, то можно найти число опытов, необходимых для реализации всех возможных со­четаний уровней факторов: N = 2^k, где N – число опытов; k – число факторов; 2 – число уровней. Если число уровней каждого фактора равно двум, то имеется полный фактор­ный эксперимент 2^k.

Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Такие таблицы называются матрица­ми планирования эксперимента.

Матрица планирования для двух факторов приведена в табл. 4.6.1. Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой.

Таблица 4.6.1

Номер опыта			у
1	-1	-1
2	+1	-1
3	-1	+1
4	+1	+1

Если для двух факторов все возможные комбинации уровней легко найти прямым перебором, то с ростом числа факторов возникает необходимость в разработке правил построения матриц. На практике обычно используются три приема, основанные на переходе от матриц меньшей раз­мерности к матрицам большей размерности.

Первый прием. При добавлении нового фак­тора каждая комбинация уровней исходного плана встреча­ется дважды: в сочетании с нижним и верхним уровнями нового фактора. Отсюда вытекает следующий прием: запи­сать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня. При переходе от эксперимента 2² к эксперименту 2³ (табл. 4.6.2) это выглядит следующим образом.

Этот прием распространяется на построение матриц любой размерности.

Таблица 4.6.2

Номер опыта				у
1	-1	-1	-1
2	+1	-1	-1
3	-1	+1	-1
4	+1	+1	-1
5	-1	-1	+1
6	+1	-1	+1
7	-1	+1	+1
8	+1	+1	+1

Второй прием. Введем правило перемножения столбцов матрицы. При построчном перемножении двух столбцов произведение единиц с одноименными знаками дает +1, а с разноименными – -1. Воспользовавшись этим правилом, для рассматриваемого случая получим вектор-столбец 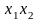в исходном плане. Далее повторим еще раз исходный план, а у столбца произведений знаки поменяем на противопо­ложные. Этот прием тоже можно перенести на построения матриц любой размерности, однако он сложнее, чем первый.

Третий прием. Он основан на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором – чередуются через два, в третьем – через четыре, в чет­вертом – через восемь и т.д. по степеням двойки.

Матрица планирования экспе­римента обладает следующими свойствами:

– симметричность относитель­но центра эксперимента – алгеб­раическая сумма элементов вектор-столбца каждого фактора равна нулю, или 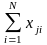, где j – номер фактора; i – номер опыта; N – число опытов.

– условие нормировки – сумма квадратов элементов каждого столбца равна числу опытов, или .

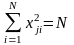– ортогональность матрицы планирования – сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, или , .

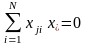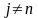– ротатабельность – точки в матрице планирования подбираются так, что точность предсказаний значений выходного пара­метра на основании математической модели одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

Таким образом, правильно составленная матрица пла­нирования эксперимента должна обладать всеми четырьмя перечисленными выше свойствами.

Составив матрицу планирования эксперимента и прове­дя N опытов, можно перейти к оценке коэффициентов ли­нейной модели.

Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель адекватна. Греческие буквы использованы для обозначения истинных значений соответствующих неизве­стных.

Эксперимент, содержащий конечное число опытов, по­зволяет получить только оценки для коэффициентов модели

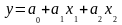. (4.6.1)

Подставив в уравнение модели известные значения 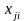факторов и результаты опытов , получим систему линейных условных уравнений, решение которой методом наименьших квадратов дает искомые оценки параметров модели:

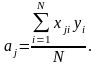(4.6.2)

Этой формулой можно воспользоваться для для вычисления коэффи­циентов а₁ и а₂:

(4.6.3)

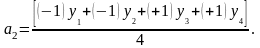(4.6.4)

Благодаря кодированию факторов расчет коэффициен­тов не представляет трудности.

Для вычисления коэффициента а₁ используется вектор-стол­бец x₁, а для вычисления а₂ – столбец x₂.

Для вычисления коэффициента а₀ найдем среднее значение равное , равное

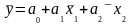, (4.6.5)

где

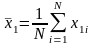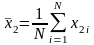; . (4.6.6)

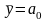В силу свойств симметрии матрицы , следова­тельно, . Чтобы все коэффициенты модели вычисля­лись по единой формуле (4.6.2), в матрицу планирования эксперимента вводят фиктивную переменную 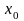, ко­торая во всех опытах принимает значение +1. Тогда линей­ная модель запишется в виде

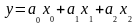, (4.6.7)

j во всех приведенных выше формулах принимает значе­ния от 0 до k.

Коэффициенты при независимых переменных указыва­ют на силу влияния факторов. Чем больше численное зна­чение коэффициента, тем большее влияние оказывает фак­тор. Если коэффициент имеет знак плюс, то с увеличением значения фактора выходная величина увеличивается, а ес­ли минус – то уменьшается.

Значение коэффициента соответствует складу данного фактора в размер выходного параметра при переходе фак­тора с нулевого уровня на верхний или нижний.

Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми – незначимыми. Чтобы установить, значим коэффициент или нет, необходимо, прежде всего, вычислить оценку дисперсии, с которой он определяется:

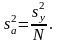(4.6.8)

Следует отметить, что с помощью полного факторного эксперимента все коэффициенты определяются с одинаковой погрешностью. Принято считать, что коэффициент регрессии значим, если выполнено условие

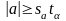, (4.6.9)

где – значение критерия Стьюдента.

В противном случае коэффициент регрессии незначим, и соответствующий член можно исключить из уравнения.

Получив уравнение регрессии, следует проверить его адекватность, т.е. способность достаточно хорошо описывать поверхность отклика. Эту проверку осуществляют с помощью критерия Фишера, который представляет собой следующее отношение:

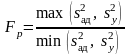, (4.6.10)

где – оценка дисперсии адекватности (4.3.7).

В числителе дроби (4.6.10) находится большая, а в знаменателе – меньшая из указанных оценок дисперсий.

Планируя эксперимент на первом этапе, обычно стремятся по­лучить линейную модель. Однако бывает так, что в вы­бранных интервалах варьирования процесс описывается нелинейной моделью.

Один из часто встречающихся видов нелинейности свя­зан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор, т.е. существует эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет оценить эффект взаимодействия. Для этого необходимо, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов.

При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обра­щаться так же как с вектор-столбцом любого фактора. Для полного факторного эксперимента 2² матрица планирования с учетом эффекта взаимодействия представлена в табл. 4.6.3.

Таблица 4.6.3

Номер опыта					у
1	+1	-1	- 1	+ 1
2	+1	+1	- 1	- 1
3	+1	-1	+ 1	-1
4	+1	+1	+ 1	+ 1

При добавлении столбцов эффектов взаимодействий все рассмотренные свойства матриц пла­нирования сохраняются.

С учетом эффекта взаимодействия математическая мо­дель при двух факторах запишется следующим образом:

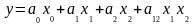. (4.6.11)

Коэффициент 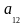вычисляется как:

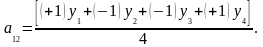(4.6.12)

Столбцы х₁ и x₂ задают планирование – по ним непо­средственно определяются условия опытов, а столбцы x₀ и х₁х₂ служат только для расчетов.

С ростом числа факторов число возможных взаимодей­ствий быстро увеличивается. Выше был рассмотрен самый про­стой случай – когда имелось одно взаимодействие. Рассмотрим теперь полный факторный эксперимент 2³.

Матрица планирования эксперимента 2³ с учетом всех возможных взаимодействий приведена в табл. 4.6.4.

Эффект взаимодействия 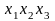определяется перемноже­нием трех столбцов , , и называется эффектом взаимо­действия второго порядка в отличие от эффектов взаимо­действия первого порядка , , .

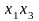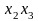Полное число всех возможных коэффициентов, включая a₀, линейные эффекты и взаимодействия всех порядков, равно числу опытов полного факторного эксперимента.

Ортогональность матрицы планирования позволяет по­лучать независимые друг от друга оценки коэффициентов. Это означает, что значение любого коэффициента не зависит от того, какие значения имеют другие коэффициенты.

Таблица 4.6.4

Номер опыта									у
1	+1	-1	-1	-1	+1	+1	+1	-1
2	+1	+1	-1	-1	-1	-1	+1	+1
3	+1	-1	+1	-1	-1	+1	-1	+1
4	+1	+1	+1	-1	+1	-1	-1	-1
5	+1	-1	-1	+1	+1	-1	-1	+1
6	+1	+1	-1	+1	-1	+1	-1	-1
7	+1	-1	+1	+1	-1	-1	+1	-1
8	+1	+1	+1	+1	+1	+1	+1	+1

Эти утверждения справедливы лишь в том слу­чае, если модель включает только линейные эффекты и эффекты взаимодействия. В реальных условиях существен­ными могут оказаться коэффициенты при квадратах факто­ров, их кубах и т.д. Для случая существенных квадра­тичных членов в двухфакторном эксперименте модель мож­но записать следующим образом:

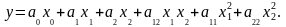(4.6.13)

Построение вектор-столбцов для 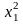и в ма­трице планирования приводит к получению единичных столбцов, совпадающих друг с другом и со столбцом a₀. Так как эти столбцы неразличимы, то нельзя сказать, за счет чего получилось значение a₀. Такая оценка a₀ называ­ется смешанной и включает в себя значение свободного члена и вклады квадратичных членов. Это символически записывается следующим образом:

(4.6.14)

где a₀ – вычисленный коэффициент, а греческими буква­ми обозначены неизвестные истинные значения свободно­го члена ₀ и квадратичных коэффициентов .

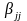По отношению к квадратичной модели для двух факто­ров получается следующая система смешивания:

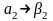, , . (4.6.15)

Очевидно, что оценки всех коэффициентов, кроме a₀, не смешаны. Таким образом, полный факторный эксперимент при варьировании факторов на двух уровнях позволяет оценить линейные эффекты и эффекты взаимодействия.

Пример 4.6.1. Рассмотрим процесс, в котором выход продукта реакции у (%) зависит от температуры реакционной смеси х₁ (°С) и концентрации реагента х₂ (%). Требуется с помощью полного факторного эксперимента найти математическое описание этого процесса в окрестности точки факторного пространства с координатами х₀₁ = 50 °С и х₀₂ = 25%. Проведено по 2 параллельных опыта при одинаковых условиях.

Решение. Математическое описание рассматриваемого процесса будем искать в виде уравнения регрессии

,

где кодированные переменные связаны с температурой и концен­трацией следующими соотношениями:

, .

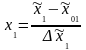При проведении полного факторного эксперимента зададимся условиями, приведенными в табл. 4.6.1.

Таблица 4.6.1

Основные характеристики плана экспериментов

Характеристика
Основной уровень……………	50	25
Интервал варьирования………..	5	1
Верхний уровень……………….	65	26
Нижний уровень……………….	45	24

Матрица планирования и результаты полного факторного эксперимента представлены в табл. 4.6.2.

На основании результатов полного факторного эксперимента рассчитаем коэффициенты регрессии, пользуясь формулами (4.6.2) ÷ (4.6.4):

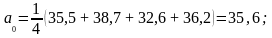
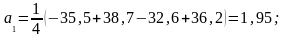
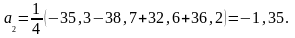
Таблица 4.6.2

Полный двухфакторный эксперимент

Номер опыта	x1	x2		, %		,%
1	–1	–1	45	24	0,50	35,5
2	+1	–1	55	24	0,72	38,7
3	–1	+1	45	26	1,28	32,6
4	+1	+1	55	26	0,82	36,2

Далее определяем оценку дисперсии среднего значения .

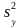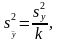
где 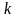– число параллельных опытов.

Оценки однородных дисперсий нескольких серий параллельных опытов можно усреднить и найти величину

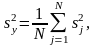
называемую оценкой дисперсии воспроизводимости. С ней связано число степеней свободы .

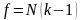На основании табл. 4.6.2:

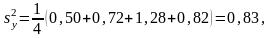
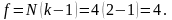
Отсюда согласно (4.6.13) оценку дисперсии среднего значения:

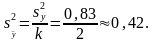
С ней также связано число степеней свободы .

Если при проведении эксперимента опыты дублируют и пользуются средними значениями функции отклика у, то при обработке экспериментальных данных следует использовать 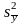. В тех случаях, когда из-за недостатка времени, трудоемкости или высокой стоимости эксперимента опыты не дублируются, при обработке экспериментальных данных используют .

Примем также, что с этой величиной связаны 4 степени свободы.

Ошибку в определении коэффициентов регрессии вычислим по формуле

.

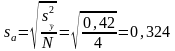Пользуясь Приложением П.1 «Процентные точки распределения Стьюдента», находим, что для доверительной вероятности Р = 0,95 (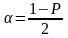 ) и 4 степеней свободы значение критерия Стьюдента t_α = 2,776. Тогда

.

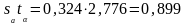Для оценки значимости коэффициентов регрессии рассмотрим следующие соотношения:

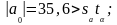
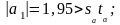
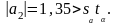
Отсюда видно, что все коэффициенты регрессии значимы. Следовательно, искомое уравнение имеет вид:

.

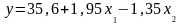Для проверки адекватности уравнения регрессии найдем расчетные значения функции отклика:

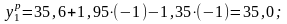
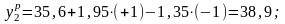
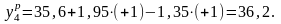
Вычислим оценку дисперсии адекватности (4.4.7):

,

где N – число опытов;

B – число коэффициентов регрессии искомой модели.

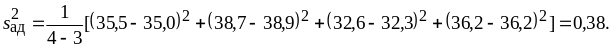
С ней связано число степеней свободы f = N – В = 4 – 3= 1. Расчетное значение критерия Фишера находим по формуле (4.4.6):

.

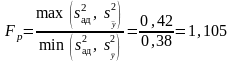Оно не превосходит значения, приведенного в Приложении П.4. «Значения (верхние значения) и (нижние значения) для различных степеней свободы f₁ и f₂» (f₁ = 4, f₂ = 1, F = 225). Следовательно, уравнение регрессии адекватно.
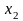
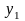
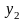
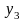
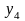
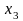
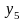
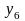
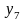
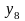
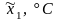
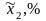