3.9. Критерии согласия

Допустим, что имеющееся статистическое рас­пределение выровнено с помощью теоретической кривой f(х). Между теоретической кривой и статистическим распределением неизбежны некоторые расхождения. Объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что подобранная кривая плохо выравнивает данное статисти­ческое распределение? Ответ на этот вопрос дают критерии согласия.

Их сущность заключается в следующем. На основании имеющегося статистического материала необходимо про­верить гипотезу Н, состоящую в том, что случайная величина X подчиняется некоторому определенному закону распределения. Пусть закон задан в виде F(х). Чтобы принять или от­бросить гипотезу H, необходимо выбрать некоторую величину W, характеризующую степень расхождения теоретического и статис­тического распределений. Ее можно выбрать различными способами; например, в качестве W взять сумму квадратов отклонений теоретических вероятностей P_i от соответствующих частот или сумму тех же квадратов с некоторыми весовыми коэффициентами, или максимальное отклонение статистической функции распределения от теоретической F(х) и т.д.

Пусть величина W выбрана.Она является случайной с законом распределения, зависящим от закона распреде­ления величины X и числа опытов п. Допустим, что этот закон известен. Тогда мера расхождения результатов опыта равна и. Если вычислить вероятность события W  u и она ока­жется малой, то гипотезу Н следует отвергнуть как мало правдоподобную; если же эта вероятность значительна, следует принять, что экспериментальные данные не противоречат гипотезе Н.

3.9.1. Критерий согласия Пирсона

Критерий Пирсона (критерий χ²-квадрат) – наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. В качестве меры расхож­дения выбрана величина

(3.9.1)

где ; – число значений в i-м разряде; r – число разрядов.

При n   закон распределения W приближается к распределению ². Распределение ² зависит от параметра k – числа степеней свободы распределения. Число степеней свободы k равно числу разрядов r минус число независимых условий (связей s), наложенных на частоты . Обычно в качестве условий выбирают следующие:

(3.9.2)

Схема применения критерия ² к оценке согласованности теоре­тического и статистического распределений сводится к следующему:

1) определяют меру расхождения ² по формуле (3.9.1);

2) опре­деляют число степеней свободы k по формуле:

k = r-s; (3.9.3)

3) по k и ² с помощью таблиц для ² находят вероятность того, что величина, имеющая распределение ² с k степенями свободы, прев­зойдет данное значение ².

Если эта вероятность весьма мала (меньше 0,1), гипотеза H отбрасывается как неправдоподобная. Если вероятность относитель­но велика, гипотезу можно признать не противоречащей опытным данным.

Пример 3.9.1. Проверить согласованность теоретического и статистического распределений для примера 3.8.1 § 3.8.

Решение. Пользуясь теоретическим нормальным законом распределе­ния с параметрами

= 0,168;  = 1,448,

находим вероятности попадания в разряды по формуле

где и – границы i-го разряда.

Составляем сравнительную таблицу чисел попаданий в разряды m_i и соответствующих значений nP_i (n = 500).

Ii	-4; -3	-3; -2	-2; 1	- 1; 0	0; 1	1; 2	2; 3	3; 4
mi	6	25	72	133	120	88	46	10
nPi	6,2	26,2	71,2	122,2	131,8	90,5	38,2	10,5

По формуле (3.9.1) определяем значение меры расхождения

Определяем число степеней свободы как число разрядов минус число наложенных связей s (в данном случае s = 3):

k = r-s = 8-3 = 5.

По таблице «Значения ² в зависимости от k и p» k = 5:

при ² = 3,000 р = 0,70;

при ² = 4,351 р = 0,50.

Следовательно, искомая вероятность р при ² = 3,94 приближенно равна 0,56. Эта вероятность малой не является; поэтому гипотезу о том, что ве­личина X распределена по нормальному закону, можно считать правдоподобной.

Пример 3.9.2. Проверить согласованность теоретического и статистиче­ского распределений для условий примера 3.8.2 § 3.8.

Решение. Значения P_i вычисляем как вероятности попадания на участки (20; 30), (30; 40) и т.д. для случайной величины, распределенной по закону равномерной плотности на отрезке (23,6; 96,9). Составляем сравнительную таблицу значений n_i и nP_i (п = 400):

Ii	20; 30	30; 40	40; 50	50; 60	60; 70	70; 80	80; 90	90; 100
mi	21	72	66	38	51	56	64	32
nPi	34,9	54,6	54,6	54,6	54,6	54,6	54,6	38,0

По формуле (3.9.1) определяем значение меры расхождения

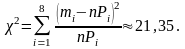
Число степеней свободы:

k = r-s = 8-3 = 5.

По таблице «Процентные точки -распределения» при k = 5 имеем:

при ² = 20,517 р = 0,001.

Следовательно, наблюденное расхождение между теоретическим и статистическим распределениями могло бы за счет чисто случайных причин появиться лишь с вероятностью р  0,001. Так как эта вероятность очень мала, следует признать экспериментальные данные противоречащими гипотезе о том, что величина X распределена по закону равномерной плотности.