3.7.2. Исключение резко отклоняющихся значений

При обработке результатов измерений очень часто возникает не­обходимость обнаружить грубые погрешности и исключить из экспе­риментальных данных соответствующие результаты. Указанная задача также требует проверки гипотез и решается статистическими методами.

Будем считать, что результаты измерений x_i имеют нормальное распределение. Чтобы проверить возможность отбросить сомнительный результат х_с (х_с – наибольший или наименьший из результатов), вы­числим величину

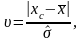(3.7.1)

где 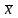и вычисляют с учетом всех n измерений.

Если все x_i распределены нормально, то распределение величины 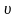не будет зависеть от параметров закона распределения x_i, но будет зависеть от числа измерений n. Имеются таблицы (таблица «Процентные точки -распределения») рас­пределения максимальных по модулю отклонений результатов измере­ний от их среднего значения

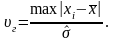(3.7.2)

Таким образом, проверяется гипотеза о том, что результат х_с не содержит грубой погрешности. Условием принятия этой гипотезы яв­ляется .

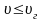Задаваясь уровнем значимости  и учитывая число измерений n, по таблице «Процентные точки -распределения» находим значение 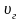. Сравниваем вычисленное по (3.7.1) значение с . Если  <  , то гипотеза не противоречит эксперимен­тальным данным. В противном случае гипотеза отклоняется, а соот­ветствующий результат х_с исключается из массива экспериментальных данных. После этого снова вычисляются оценки и , а описанная выше процедура может быть повторена для следующего подозревае­мого результата.

Пример 3.7.3. При условиях, заданных в примере 3.7.1, необходимо про­верить гипотезу, состоящую в том, что наибольший результат измере­ний x_с = 7,8 не содержит грубой погрешности.

Решение. Вычислим

Принимаем уровень значимости  = 0,05. Для n = 10 по таблице «Процентные точки -распределения» находим = 2,414. Так как  >  , то гипотеза отклоняется, т.е. следует считать, что результат x_с = 7,8 содержит грубую погрешность, а следовательно, должен быть исключен из экспериментальных данных.

3.8. Построение эмпирических распределений

При исследовании случайных процессов не­обходимо знать не только числовые характеристики случайных ве­личин, но законы их распределения. Поэтому необходимо знать закон распределения случайной величины по статистическим данным, полученным в эксперименте. Пусть в результате экспери­мента получено п значений случайной величины х₁, х₂, ..., х_п (ста­тистический ряд). Под статистической функцией распределения случайной величины X понимают частоту события X < х в данном статистическом интервале.

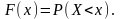(3.8.1)

Статистическая функция распределения любой случайной вели­чины является прерывной сту­пенчатой функцией, скачки которой соответствуют наблюдаемым значениям случайной величины (рис. 3.8.1); они равны частотам появ­ления этих значений 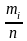, где 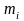– число появлений i-ro значения случайной величины в п опытах.

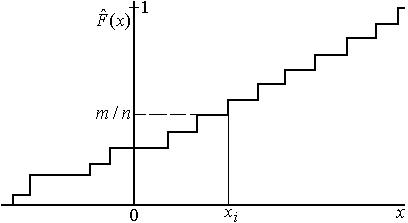
Рис. 3.8.1. Статистическая функция распределения

Кроме статистического интегрального закона распределения вводят понятие статистического дифференциального закона распределения, под которым понимают зависимость плотности рас­пределения наблюдаемых значений случайной величины

(3.8.2)

где – частота появления случайной величины в интерва­ле 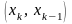в п опытах. Для наглядности статистический диффе­ренциальный закон распределения представляют гистограммой (рис. 3.8.2).

Для определения законов распределения случайной величины X проводят эксперимент, получают n значения случайной величины, по ним строят статистические законы распределения. При n   эмпирическая функция распределения приближается к истинной функции рас­пределения. В реальности число опытов ограничено. Поэтому не­обходимо определять закон распределения случайной величины по ограниченному числу опытов. При обработке ограниченного по объему статистического материала приходится решать вопрос о том, как подобрать для данного статистического ряда тео­ретическую кривую распределения, выражающую лишь существен­ные черты статистического материала, а не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача подбора теоретической кривой распределения называется задачей выравнивания статистических рядов.

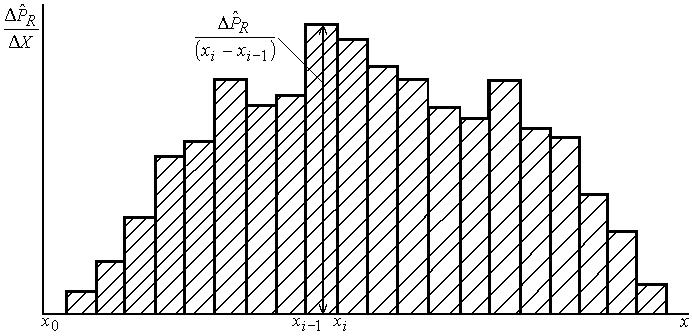
Рис. 3.8.2. Гистограмма статистического диф­ференциального зако­на

распределения

Принципиальный вид теоретической кривой вы­бирается либо заранее из соображений, связанных с существом задачи, либо исходя из внешнего вида статистического рас­пределения. Аналитическое выражение выбранной кривой распреде­ления зависит от некоторых параметров; задача выравнивания ста­тистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистичес­ким и теоретическим распределениями наилучшее.

Любая выбранная аналитическая функция f(х), с помощью ко­торой выравнивается статистическое распределение, должна об­ладать основными свойствами плотности распределения:

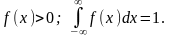(3.8.3)

Допустим, что функция f(х), с помощью которой выравнивается данное статисти­ческое распределение, выбрана. В выражение этой функции входит несколько параметров a, b, .... Требуется подобрать эти параметры так, чтобы функция f(х) наилучшим образом описывала данный статистичес­кий материал. Наиболее часто для решения этой задачи применяется метод моментов. Согласно ему, параметры а, b, ... выбираются так, чтобы несколько важнейших числовых характерис­тик теоретического распределения были равны соответ­ствующим статистическим характеристикам. Например, если теоретическая кривая f(х) зависит только от двух параметров а и b, они выбираются так, чтобы математиче­ское ожидание и дисперсия 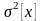теоретического распределения совпадали с соответствующими статистическими характеристикам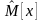и и 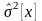. Если кривая f(х) зависит от трех параметров, можно по­добрать их так, чтобы совпали первые три момента и т.д.

Пример 3.8.1. Пусть в результате эксперимента над случайной величиной X, которая может принимать значения в интервале (-; +), получен статистический ряд (500 измерений):

Ii	-4; -3	-3; -2	-2; -1	-1; 0	0; 1	1; 2	2; 3	3; 4
ni	6	25	72	133	120	88	46	10
Pi	0,012	0,05	0,144	0,266	0,24	0,176	0,092	0,02

Требуется выровнять это распределение при помощи нормального закона:

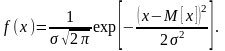
Решение. Определим статистические моменты случайной величины X – матема­тическое ожидание и дисперсию:

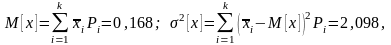
где 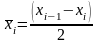– представитель i-го разряда; 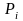– частота i-го разряда; k – число разрядов.

Выберем параметры и  нормального закона так, чтобы выполнялись условия:

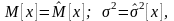
т.е. = 0,168;  = 1,448. Тогда получим:

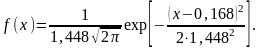
Используя таблицу «Распределение функции 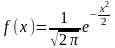», вычислим значения на границах рядов:

x	-4	-3	-2	-1	0	1	2	3	4
	0,004	0,025	0,090	0,199	0,274	0,234	0,124	0,041	0,008

На рис. 3.8.3 приведены гистограмма и выравнивающая ее кривая распределения.

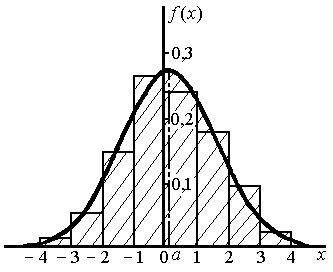
Рис. 3.8.3. Гистограмма и выравнивающая кривая

Пример 3.8.2. С целью исследования закона распределения ошибки из­мерения дальности с помощью радиодальномера произведено 400 измерений дальности. Результаты опытов представлены в виде статистического ряда:

Ii	20; 30	30; 40	40; 50	50; 60	60; 70	70; 80	80; 90	90; 100
ni	21	72	66	38	51	56	64	32
Pi	0,052	0,180	0,165	0,095	0,128	0,140	0,160	0,080

Выровнять статистический ряд с помощью закона равномерной плотности.

Решение. Закон равномерной плотности выражается формулой:

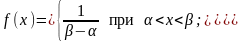
Выражения для математического ожидания и дисперсии для закона равномерной плотности имеют вид:

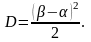
Для того чтобы упростить вычисления, перенесем начало отсчета в точку x₀ = 60 и примем за представителя каждого разряда его середину. Ряд распределения примет вид:

	-35	-25	-15	-5	5	15	25	35
Pi	0,052	0,180	0,165	0,095	0,128	0,140	0,160	0,080

где – среднее для разряда значение ошибки радиодальномера X' при но­вом начале отсчета.

Приближенное значение статистического среднего ошибки X' равно:

Второй статистический момент величины X' равен:

откуда статистическая дисперсия:

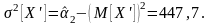
Переходя к прежнему началу отсчета, получим новое статистическое среднее:

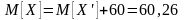
и ту же статистическую дисперсию

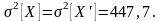
Параметры закона равномерной плот­ности определяются уравнениями:

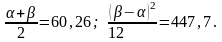
Решая эти уравнения относительно  и , имеем:

,

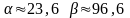откуда

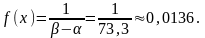
На рис. 3.8.4 показаны гистограмма и выравнивающий ее закон равномерной плотности .

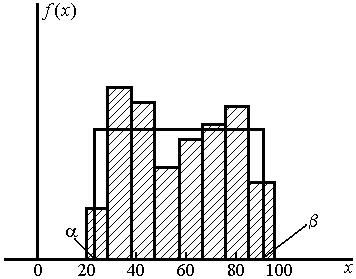
Рис. 3.8.4. Гистограмма и выравнивающая кривая

На практике часто случается так, что заранее закон теоретический закон распределения не известен. Поэтому рассмотрим вопрос о том, каким выбрать теоретическое распределе­ние по статистическому ряду, когда заранее вид теоретического распределения не известен. В этом случае пользуются системой кривых Пирсона (рис. 3.8.5).

Для применения кривых на рис. 3.8.5 необходимо знать значения ₁ и ₂, которые определяются как

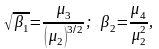
где ₂, ₃, ₄ – второй, третий, четвертый центральные моменты случайной величины соответственно. Однако значения ₁ и ₂ обычно неизвестны. Поэтому для того, чтобы узнать, будут ли над­лежащим образом описаны полученные данные (статистический ряд) одним из показанных на рис. 3.8.5 распределений, необходимо найти выборочные оценк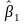и и .

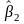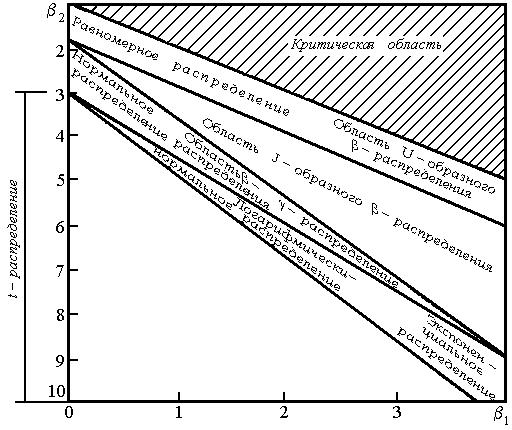
Рис 3.8.5. Система кривых Пирсона

Для определения и необходимо найти статистические моменты , , 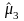по следующим формулам:

. (3.8.4)

Определив , и, нанеся эту точку на графики рис. 3.8.5, можно узнать, какое распределение наиболее подходит для выравнивания статистического ряда.

При применении этого метода необходимо следующие ограничения:

1) и являются лишь оценками для ₁ и ₂ и подвержены колебаниям от выборки к выборке, поэтому этим методом пользоваться не рекомендуется при малом числе на­блюдений (например, меньше 200);

2) в общем случае форма распре­деления не определяется однозначно его нормированными показа­телями асимметрии (₁) и островершинности (₂).