3.2. Обработка результатов измерений. Оценки измеряемой величины

Измерения являются средством получения информации о тех или иных свойствах реальных физических объектов, о закономерностях протекающих процессов и т.п. Разнооб­разие задач, решаемых с помощью измерений, определяет разнообразие видов обработки результатов измерений. Так как все измерения сопровождаются случайными по­грешностями, то обработка результатов измерений всегда включает в себя операции над случайными величинами или случайными процессами, выполняемые на основе мето­дов теории вероятностей и математической статистики.

Пример 3.2.1. Пусть производятся прямые из­мерения физической величины, истинное значе­ние которой равно а. Если выполнено единственное изме­рение, результат которого равен x, то задача обработки не возникает. Экспериментатор может только оценить пре­дельно допускаемую погрешность на основе норм на мет­рологические характеристики используемых средств изме­рений. Предположим, что в тех же условиях вы­полнены п аналогичных измерений, результаты которых равны х₁, х₂, ..., х_п.

Разность 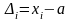представляет собой погрешность i-го измерения и является случайной величиной. Очевидно, что первая задача экспериментатора состоит в нахождении оценки измеряемой величины а. Эта оценка может быть получена только путем выполнения математических опе­раций над результатами х₁, х₂, ..., х_п и, следовательно, яв­ляется случайной величиной, которая должна в некотором смысле наилучшим образом приближаться к значению из­меряемой величины. Таким образом, прежде чем получить формулу для вычисления оценки , необходимо сформули­ровать критерий, характеризующий качество той или иной оценки.

Дополнительная измерительная информация, полученная путем проведения п измерений, дает возможность более точно оценить значение измеряемой величины, оценить параметры закона распределения случайной погрешности, проверить некоторые предположения (гипотезы) относи­тельно этих величин.

Пример 3.2.2. Производятся совместные измерения темпе­ратуры t терморезистора и его сопротивления R_t при этой температуре с целью установить зависимость R_t = R(t). Предположим, что известен линейный характер этой зависимости, т.е.

, (3.2.1)

где 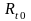– сопротивление терморезистора при температуре 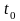;  – температурный коэффициент сопротивления.

Для решения поставленной задачи необходимо прове­дение минимум двух опытов при температурах t₁ и t₂, ре­зультаты которых можно представить в виде следующей системы уравнений:

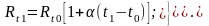(3.2.2)

В результате решения системы (3.2.2) находим оценки параметров R_t0 и . Очевидно, что, кроме решения ука­занной системы уравнений, никакие другие задачи, связан­ные с обработкой результатов измерений, в данном случае не возникают. Положение существенно меняется, если, кроме двух описанных выше измерений, выполняются еще дополнительные измерения при других значениях тем­пературы. Пусть проведено п опытов при разных темпе­ратурах, результаты которых запишем в виде системы п уравнений:

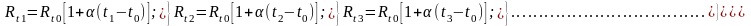(3.2.3)

Так как результаты измерений являются случайными величинами, то система уравнений (3.2.3) является несов­местной, т.е. нет таких значений параметров R_t0 и , ко­торые удовлетворяли бы всем уравнениям системы. Поэто­му и в данном случае экспериментатор должен найти такие оценки 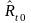и искомых параметров, которые в не­котором смысле наилучшим образом приближали бы полученную линейную функцию ко всей совокупности экс­периментальных данных.

Как и в предыдущем примере, получение путем прове­дения дополнительных опытов измерительной информации позволяет повысить точность оценок искомых параметров линейной зависимости, оценить уровень погрешности из­мерений и погрешностей полученных оценок параметров, проверить те или иные гипотезы и т.п.

Чтобы оценка некоторой измеряемой величины (па­раметра) а была в каком-то смысле «доброкачественной», она должна удовлетворять следующим требованиям: оценка должна быть состоятельной, несмещенной и эффективной.

Оценка называется состоятельной, если при увеличении числа опытов п оценка приближается к истинному зна­чению а.

Оценка называется несмещенной, если ее математическое ожидание М[ ] равно истинному значению а, т.е. М[ ] = а. Очевидно, что если оценка несмещенная, то она не содержит систематической погрешности.

Оценка называется эффективной, если по сравнению с другими она обладает наименьшей дисперсией, т.e. D[ ] = min.

На практике не всегда получают оценки, удовлетворя­ющие всем перечисленным требованиям. Для упрощения вычислений иногда допускают некоторую смещенность оценки или используют, строго говоря, неэффективную оценку, однако во всех подобных случаях необходимо оце­нить степень ухудшения получаемой оценки по сравнению с наилучшей.

Получение «доброкачественных» оценок требует опре­деления критерия их сравнения. Если такой критерий ус­тановлен, то наилучшей оценкой будет та, которая обеспе­чит экстремум этого критерия.

Наибольшее распространение в практике получили сле­дующие методы нахождения «доброкачественных» оценок: наименьших квадратов и максимального правдоподобия.

В методе наименьших квадратов в качестве критерия сравнения оценок используется сумма квадратов отклоне­ний результатов измерений от полученной оценки измеряе­мой величины (или функции). Так, в примере 1 наилучшая оценка а должна удовлетворять условию

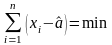, (3.2.4)

а в примере 2 условие оптимальности оценок R_t0 и при­мет вид

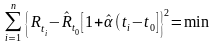. (3.2.5)

В методе максимального правдоподобия в качестве критерия оптимальности оценок используется функция правдоподобия, представляющая собой плотность вероятности всей совокупности экспериментальных данных. Искомые оценки находятся из условия максимума функции правдоподобия, что фактически соответствует максимуму вероятности получения именно тех результатов измерений, которые были получены в опытах. Вычисление функции правдоподобия требует знания вида закона распределения погрешности измерений. В этом и состоит принципиальное отличие критерия максимального правдоподобия от критерия наименьших квадратов. Оценки, получаемые этими методами, совпадают в том случае, когда погрешность имеет нормальный закон распре­деления.

Наряду с получением оценки искомой величины в виде одного числа (так называемое точечное оценивание) ши­рокое распространение получило оценивание с помощью доверительных интервалов.

Доверительным интервалом называется интервал зна­чений оцениваемой величины, который с заданной веро­ятностью (доверительной вероятностью) накрывает истинное значение этой величины. Доверительный интервал яв­ляется случайным интервалом: случайно его положение, определяемое точечной оценкой величины, случайна и дли­на интервала, вычисляемая, как правило, по опытным дан­ным.

Необходимо обратить внимание на то, что окончательные результаты обработки измерительной информации, представляемые в виде чисел, должны быть округлены в соответствии с ус­тановленными правилами. В основе правил округления ле­жит утверждение, что числовое значение результата изме­рения должно быть представлено так, чтобы оно оканчи­валось десятичным знаком того же разряда, что и значение его погрешности. Большее число разрядов нецелесообраз­но, так как неопределенность результата, определяемая погрешностью, при этом не уменьшится. При уменьшении числа разрядов неопределенность результата увеличится.