1.7.1. Цифровые коды

В зависимости от значения основания кода m их называют двоичными (m = 2), десятеричными (m = 10) и т.д.

Двоичные коды основаны на использовании двоичной системы счисления. Это позиционная система счисления, в которой числовое значение символа зависит от его места в числе. Ее главным преимуществом является несложная аппаратурная реализация логических операций и арифметических действий, а также устройств передачи и запоминания сообщений.

Двоичные коды можно разделить на две группы. К первой группе относятся коды, использующие все возможные комбинации, – неизбыточные коды. Ко второй группе относятся коды, использующие лишь часть всех возможных комбинаций, – избыточные коды. Оставшаяся часть ком­бинаций используется для обнаружения и исправления ошибок, возникающих при передаче информации. В этих кодах количество разрядов кодовых комбинаций можно условно разделить на определенное число разрядов, предназначенных для полезной информации (информационные разряды), и число разрядов, предназначенных для обнаружения или исправления ошибок (проверочные разряды).

Если в двоичном коде длина всех кодовых комбинаций одинакова, то такие коды называются равномерными. Например, код, состоящий из комбинаций 001, 011, 111, является равномерным; код 1, 11, 110 нерав­номерный. В телеизмерении применяются равномерные коды (n = const) из-за удобства передачи, расшифровки и защиты от ложных кодовых комбинаций.

Избыточные коды, в которых определенные разряды кодовых комбинаций отводятся для информационных и проверочных символов, являются разделимыми.

Неразделимые коды не имеют четкого разделения ко­довой комбинации на информационные и проверочные символы. Наибольшее распространение получили раздели­мые равномерные коды, у которых проверочные символы опре­деляются в результате проведения линейных операций над определенными информационными символами. Обычно та­кой операцией является сложение по модулю 2. Указанные коды называются систематическими.

Основными характеристиками кодов являются основание кода, длина кода, мощность кода, полное число кодовых комбинаций, число информационных разрядов, число проверочных разрядов, избыточность кода, кодовое расстояние.

Основание кода m – число различных цифр (букв), из которых строится код. Для двоичных кодов m = 2. Длина кода n – число разрядов, составляющих кодовую комби­нацию. Мощность кода N_p – число кодовых комбинаций, используемых для передачи информации. Полное число ко­довых комбинаций N – число всех возможных комбина­ций, равное mⁿ (для двоичных кодов N = 2ⁿ), Число информационных разрядов k связано с мощностью кода со­отношением N_p = m^k (для двоичных кодов N_р = 2^k).

Число проверочных разрядов r = n-k – число разрядов кодовой комбинации, необходимых для коррекции оши­бок. Это число характеризует абсолютную избыточность кода.

Кодовое расстояние d между кодовыми комбинациями – число соответствующих разрядов с различными символами. Так, например, для комбинации 101 и 011 d = 2. Для кода в целом важной характеристикой является минимальное кодовое расстояние d_min.

Для десятичных чисел во многих случаях используются более слож­ные коды, основанные на раздельном кодировании каждой десятичной цифры и полуразрядном представлении кодовых комбинаций, соответст­вующих отдельным десятичным цифрам числа. К таким простейшим ко­дам относятся единично-десятичный код, используемый при наборе но­мера абонента номеронабирателем в автоматических телефонных систе­мах. Каждая цифра десятичного числа в этом коде передается соответст­вующим числом импульсов.

В системах измерений, цифровых и других устройствах широкое применение получил двоично-десятичный код. В двоично-десятичных кодах каждая десятичная цифра представляется группой цифр, состоящей из четырех двухпозиционных разрядов. Такая группа позволяет сформиро­вать 16 различных комбинаций. В десятичной системе используются только 10 цифр, т.е. шесть комбинаций являются избыточными. Так как избыточными могут быть любые шесть комбинаций, то это приводит к большому числу вариантов построения двоично-десятичных кодов.

Предположим, что каждая десятичная цифра представляется в виде

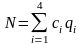, (1.7.1)

где 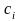равно 0 или 1, a 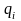– веса соответствующих разрядов.

Очевидно, что для кодирования цифр от 0 до 9 необходимо, чтобы .

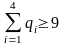Двоично-десятичные коды строятся с учетом следующих условий:

1) вес наименьшей значащей цифры q₁ равен 1;

2) вес второй значащей цифры q₂ равен 1 или 2;

3) вес, соответствующий двум оставшимся цифрам кода, , если q₂ = l, или ,если q₂ = 2;

4) совокупность весов должна удовлетворять соотношению .

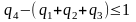В соответствии с этими условиями можно сформировать 17 кодов со следующими весами разрядов:

8–4–2–1 3–3–2–1

7–4–2–1 6–2–2–1

6–4–2–1 5–2–2–1

5–4–2–1 4–2–2–1

4–4–2–1 6–3–1–1

7–3–2–1 5–3–1–1

6–3–2–1 4–3–1–1

5–3–2–1 5–2–1–1

4–3–2–1

Так, например, при использовании кода 4–2–2–1 число 138 будет закодировано в виде 0001 0011 1110.

Все двоично-десятичные коды, кроме кода 8–4–2–1, не имеют однозначности в отображении десятичных чисел. Необходимая однозначность достигается только соответствующим построением устройств кодирования и декодирования.

Двоично-десятичные коды обладают небольшой избыточностью, что можно использовать для обнаружения некоторых ошибок. Однако при этом выявляются не все даже простые однократные ошибки, а только те из них, которые приводят к появлению неиспользуемых кодовых комбинаций.

В двоичном коде при переходе от изображения одного числа к изображению соседнего большего или соседнего меньшего числа может происходить одновременно изменение цифр в нескольких разрядах. Это может явиться источником значительных ошибок при некоторых способах кодирования непрерывных сообщений, например при геометрическом кодировании угловых и линейных перемещений.

Эффективным средством борьбы с такого рода ошибками (ошибками считывания) является использование специальных кодов, носящих название отраженных (рефлексных). Отличительная особенность этих кодов состоит в том, что соседние кодовые комбинации различаются цифрой только в одном разряде. Среди отраженных кодов наибольшее распространение получил код Грея, так как он легко преобразуется в двоичный код. В табл. 1.7.1 приведен код Грея для кодирования 16 сообщений – чисел от 0 до 15.

Таблица 1.7.1

Десятичное число	Код Грея	Десятичное число	Код Грея
0	0000	8	1100
1	0001	9	1101
2	0011	10	1111
3	0010	11	1110
4	0110	12	1010
5	0111	13	1011
6	0101	14	1001
7	0100	15	1000

Недостатком кода Грея и других отраженных кодов является их невесомость, т.е. в них вес единицы не определяется номером разряда. Это затрудняет их кодирование и обработку с помощью ЭВМ, поэтому перед такими операциями отражений код преобразуют в простой двоичный код. Перевод кода Грея в обычный двоичный код осуществляется по следующим правилам: первая единица со стороны старших разрядов остается без изменения, последующие цифры остаются без изменения, если число единиц, им предшествовавших, четно, и инвертируются, если число единиц нечетно.

Двоичный код, для которого общее число комбинаций N = 2ⁿ, единичный, единично-десятичный, двоично-десятичный и отраженный коды называются обыкновенными (непомехозащищенными) кодами. В них искажение любого разряда кодовой комбинации не может быть обнаружено.

Помехозащищенными, или корректирующими, кодами называются коды, позволяющие обнаружить или исправить ошибки в кодовых ком­бинациях.

Как известно из теории информации, введение избыточности в сообщение является средством повышения его помехоустойчивости. При построении избыточного кода для передачи информации используется лишь часть всех возможных комбинаций (разрешенные комбинации), отличающихся друг от друга более чем в одном разряде. Все остальные комбинации используются и относятся к числу запрещенных. Это значит, что из п разрядов кодовой комбинации для передачи информации используются k разрядов. Следовательно, из общего числа N=2ⁿ возможных кодовых комбинаций для передачи информации используется только N_p = 2^k разрешенных комбинаций. Остальные N-N_p = 2ⁿ-2^k комбинаций являются запрещенными.

Так как разрешенные комбинации отличаются более чем в одном разряде, то ошибка в одном разряде (случай­ная замена одного символа другим) приводит к замене разрешенной комбинации запрещенной. Это позволяет об­наружить, а иногда и исправить ошибку. При достаточно большом отличии разрешенных комбинаций друг от друга можно обнаружить двукратную, трехкратную ошибку и т.д.

Для использования кода в качестве корректирующего множество запрещенных кодовых комбинаций разбивается на N_p непересекающихся подмножеств, каждое из которых ставится в соответствие одной из разрешенных комбинаций. Однако, поскольку запрещенная кодовая комбинация, относящаяся к одному из подмножеств, может быть получена в результате искажения любой разрешенной комбинации, исправляются не все ошибки.

Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться данным кодом. Большинство кодов предназначено для исправления взаимно неза­висимых ошибок определенной кратности и пачек (пакетов) ошибок.

Кратностью ошибки называется количество искаженных разрядов в кодовой комбинации. Так как вероятность ошибки обычно невелика, то вероятности многократных незави­симых ошибок пренебрежимо малы. Поэтому наибольшее применение на практике нашли коды, исправляющие одно­кратные (реже двукратные) ошибки.

Для оценки различия между комбинациями данного кода используется минимальное кодовое расстояние d_min, характеризующее способность кода обнаруживать и исправлять определенные ошибки.

Неизбыточный двоичный код имеет минимальное кодовое расстояние d_min = l. Можно показать, что обнаружение всех ошибок кратности до t₀ возможно, если d_min удовлетворяет условию

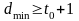. (1.7.2)

Для исправления ошибок кратности t_и кодовое расстоя­ние должно удовлетворять условию

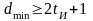. (1.7.3)

Для исправления всех ошибок кратности до 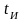и одно­временного обнаружения всех ошибок кратности не более t₀ кодовое расстояние должно быть

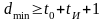. (1.7.4)

Идея построения кода с заданной корректирующей способностью, следовательно, заключается во внесении в него такой избыточности, которая обеспечила бы расстояние между любыми кодовыми комбинациями данного кода не менее d_min, определяемой приведенными формулами.

Для обнаружения однократных ошибок чаще всего используется код с одной проверкой на четность. Данный код независимо от длины кодовой комбинации содержит всего один проверочный разряд. Символ в этом разряде выбирается таким, чтобы его сумма по модулю 2 со всеми инфор­мационными символами равнялась нулю. Например, простые комбинации 00101 и 10101 при кодировании их кодом с одной проверкой на четность выглядят соответственно 001010 и 101011.

Признаком искажения кодовой комбинации является нечетность числа единиц в принятой комбинации. Данный код позволяет только обнаруживать однократные ошибки и все ошибки нечетной кратности. Данный код имеет минимальное кодовое расстояние d_min = 2 и относительную избыточность .

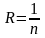Другим кодом, обнаруживающим ошибки, является код с простым повторением. В основу построения этого кода положен метод повторения исходной кодовой комбинации. При декодировании производится сравнение первой (информационной) и второй (проверочной) частей кодовой комбинации. При отсутствии совпадения фиксируется наличие ошибки в кодовой комбинации. Помехоустойчивость этого кода выше помехоустойчивости кода с проверкой на четность, так как он позволяет обнаруживать любые ошибки, за исключением одновременных ошибок в "парных" элементах, стоящих на одних и тех же позициях в первой и второй частях комбинаций.

Рассмотренные выше блочные коды позволяют только обнаруживать ошибки. Для исправления ошибок необходимо ввести r проверочных разрядов, число которых определяется требованиями к корректирующей способности кода.

При малой вероятности появления независимых ошибок наиболее часто встает задача исправления одиночного искажения. Идея кода с исправлением однократных ошибок была предложена Хэммингом. Ее сущность состоит в том, что производятся многократные проверки на четность различных вариантов сумм разрядов полученной кодовой комбинации, в результате которых получается двоичный код номера искаженного разряда. Таким образом, если при проверке на четность получен нуль, то это означает, что в данной комбинации нет ошибок.

Создание корректирующего кода, обладающего указанными свойствами, требует решения следующих вопросов:

1) определения необходимого количества проверочных разрядов;

2) формирования правила проверки, позволяющего исправить любую однократную ошибку;

3) установления номеров разрядов, на которых располагаются проверочные символы.

Число проверок должно быть равно числу r проверочных разрядов. Результаты проверок записываются в виде r-разрядного двоичного числа, указывающего номер искаженного разряда. Так как всего разрядов n, то должно удовлетворяться соотношение

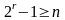. (1.7.5)

Поскольку код, полученный в результате проверок, должен указывать номер искаженного разряда, то правила проверки формулируются следующим образом:

1) все проверки заключаются в вычислении суммы по модулю 2 соответствующих разрядов;

2) при первой проверке выбираются те разряды, двоичные представления номеров позиций которых содержат единицу в первом разряде, т.е. 1, 3, 5, 7, 9-й, ... разряды;

3) при второй проверке выбираются те разряды, двоичные представления номеров позиций которых содержат единицу во втором разряде, т.е. 2, 3, 6, 7, 10-й, ... разряды;

4) при третьей проверке выбираются 4, 5, 6, 7, 12, 13-й... разряды и т.д.

Место расположения проверочных разрядов в кодовой комбинации в принципе может быть выбрано произвольно, однако практически более удобным является случай, когда каждый проверочный символ участвует только в одной проверке. Обычно проверочные символы размещаются в разрядах, номера которых равны целой степени числа 2, т.е. в разрядах 1, 2, 4, 8 и т.д.

В качестве примера построим код Хэмминга для передачи 16 сообщений – чисел от 0 до 15.

Так как N_P = 16, то необходимое число информационных разрядов k = 4. В соответствии с (1.7.5) необходимое число проверочных разрядов r = 3, а длина кода n = k + r = 7. Позиции 1, 2 и 4 будем использовать для проверочных символов, на остальных (информационных) разместим двоичные представления чисел от 0 до 15. Полученный код Хэмминга приведен в табл. 1.7.2.

Таблица 1.7.2

Десятичное число	Символы кода для позиций
	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	1	1	0	1	0	0	1
2	0	1	0	1	0	1	0
3	1	0	0	0	0	1	1
4	1	0	0	1	1	0	0
5	0	1	0	0	1	0	1
6	1	1	0	0	1	1	0
7	0	0	0	1	1	1	1
8	1	1	1	0	0	0	0
9	0	0	1	1	0	0	1
10	1	0	1	1	0	1	0
11	0	1	1	0	0	1	1
12	0	1	1	1	1	0	0
13	1	0	1	0	1	0	1
14	0	0	1	0	1	1	0
15	1	1	1	1	1	1	1

Предположим, что в результате действия помех приня­та запрещенная кодовая комбинация 0111110. В соответствии с принятой нумерацией позиций проведем три провер­ки на четность следующих позиций: 1) 1, 3, 5, 7; 2) 2, 3, 6, 7; 3) 4, 5, 6, 7. Результаты проверок запишем справа нале­во в виде числа 110, которое указывает, что искажен шес­той разряд, т.е. правильной является комбинация 0111100, соответствующая числу 12.

Рассмотренный код имеет минимальное кодовое рассто­яние d_min = 3 и позволяет исправлять любые однократные ошибки.

Таким образом, помехоустойчивое кодирование являет­ся эффективным средством повышения достоверности полу­чаемой информации.