6.9. Суммирование погрешностей измерительных устройств

Результирующая погрешность измерительного преобразователя складывается из большого числа отдельных составляющих. Каждая из составляющих может быть найдена расчетным или экспериментальным путем, а суммирование их должно быть произведено по определенным правилам.

Для вычисления результирующей погрешности существует два подхода. Первый предлагает арифметически суммировать абсолютные максимальные значения всех составляющих погрешности, второй – суммировать погрешности геометрически.

Пусть устройство имеет только десять составляющих погрешности, каждая из которых может принимать значения -5, -4, ..., 0, ..., +4 и +5, т.е. 11 различных значений. Тогда общее число возможных комбинаций равно 11¹⁰. Суммирование максимальных абсолютных значений соответствует только двум случаям, когда все погрешности равны или +5, или -5. Если принять, что все комбинации равновероятны, то вероятность этих случаев равна

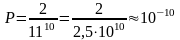. (6.9.1)

Таким образом, подобное совпадение может произойти в среднем один раз из 10¹⁰ случаев, т.е. оно практически не встретится не только за весь срок службы одного измерительного устройства, но даже и при одновременной эксплуатации многих тысяч измерительных устройств. Вследствие этого неправомерность арифметического суммирования очевидна.

Однако и геометрическое суммирование правомерно, строго говоря, только в единственном случае, когда все составляющие имеют один и тот же закон распределения вероятностей, совпадающий к тому же с законом распределения результирующей погрешности. В связи с этим сторонники геометрического суммирования предлагают принять допущение, что все погрешности измерительных устройств являются условно-случайными и распределены по нормальному закону.

6.10. Статистическое суммирование погрешностей при наличии корреляции

При выборе того или иного метода суммирования составляющих погрешности определяющим признаком является разделение погрешностей по признаку их сильной или слабой взаимной корреляционной связи.

Известно, например, что магнитоэлектрический измерительный механизм при изменении температуры имеет положительную погрешность от уменьшения жесткости пружинки и отрицательную от уменьшения индукции магнита. При случайном характере колебаний температуры обе эти составляющие погрешности проявляются как случайные. Однако, несмотря на случайный характер появления этих погрешностей во времени, они жестко связаны (сильно коррелированы) между собой, так как при любых случайных колебаниях положительному значению одной из них всегда сопутствует отрицательное значение другой. Поэтому, хотя появление этих составляющих во времени имеет случайный характер, при суммировании они должны всегда вычитаться друг из друга, а не складываться. Геометрическое же суммирование этих составляющих совершенно неправомерно.

Другим наглядным примером связанных между собой случайных погрешностей являются погрешности отдельных измерительных преобразователей от случайных колебаний напряжения источника питания. Пусть измерительное устройство содержит несколько усилительных каскадов, питающихся от общего источника. Если коэффициент усиления каждого каскада зависит от питающего напряжения, возрастая, например, на 1% при увеличении напряжения питания на 1 В, то погрешности, вносимые в результат измерения, жестко коррелированы между собой. При повышении напряжения все они положительны, а при уменьшении – все отрицательны. Поэтому при определении результирующей погрешности все эти составляющие должны суммироваться алгебраически, а не геометрически.

Однако те же самые погрешности от изменения температуры или напряжения питания могут быть слабо связанными или совсем не связанными между собой. Например, температура датчика, установленного в точке измерения, может изменяться по совершенно другому закону, чем температура остального измерительного устройства. Изменение напряжения питания аппаратуры, установленной на спутнике, никак не связано с изменением напряжения в сети, от которой питается наземная часть измерительного устройства, и т.д.

Во всех подобных случаях составляющие погрешности являются независимыми, некоррелированными между собой и должны суммироваться по правилам сложения независимых случайных погрешностей, т.е. геометрически.

Теория вероятностей для дисперсии суммы двух случайных величин, как известно, дает следующее выражение:

(6.10.1)

отсюда среднеквадратическая результирующая погрешность

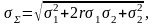(6.10.2)

где 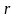– коэффициент корреляции этих величин.

Исходя из этого общего выражения, при сильной взаимосвязи слу­чайных величин, когда коэффициент корреляции 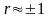, получаем

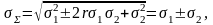(6.10.3)

т.е. правило алгебраического суммирования составляющих.

При слабой корреляционной связи или ее отсутствии, т.е. при 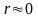, для независимых или слабо зависимых величин имеем

(6.10.4)

т.е. правило геометрического суммирования составляющих.

В современных измерительных устройствах общее число подлежащих суммированию составляющих погрешности может достигать 20  50. В этих условиях точный учет всех взаимных корреляционных связей весьма сложен. При этом часто нет необходимости определять суммарные погрешности каждого преобразователя в отдельности, определению подлежит общая погрешность измерительного устройства в целом. В данном случае все 50 составляющих могут суммироваться безотносительно к тому, какому из преобразователей они обязаны своим происхождением. Поэтому можно использовать следующий упрощенный подход к определению взаимной корреляции, погрешностей.

Если ряд погрешностей одного или нескольких преобразователей вызывается одной и той же общей причиной, в результате чего они оказываются достаточно сильно коррелированными, то коэффициент их взаимной корреляции принимается равным +1 или -1.

Если погрешности вызываются причинами, не имеющими между собой явной связи, то их корреляция принимается равной нулю. Никакие промежуточные значения коэффициента корреляции в расчете не используются.

Исходя из этого, для суммирования погрешностей, прежде всего, надо выделить группы погрешностей, сильно коррелированных между собой. Вследствие жесткой взаимной корреляции и общей причины, вызывающей все эти погрешности, они будут распределены по одному и тому же закону, а форма результирующего закона распределения будет также соответствовать этому закону. Поэтому внутри каждой из этих групп погрешности должны складываться алгебраически с уче­том их знаков.

Результирующие погрешности, полученные после суммирования в каждой из групп, уже не имеют между собой заметных корреляционных связей и должны рассматриваться как статистически независимые. Поэтому безотносительно к тому, являются ли эти погрешности в обычном смысле систематическими или случайными, они должны складываться по правилам суммирования случайных погрешностей.