1.4. Спектр периодических сигналов

Совокупность амплитуд гармонических составляющих, на которые разложен сигнал, образуют спектр амплитуд. Сложный периодический сигнал обладает дискретным (линейчатым) спектром, графически изображающимся в виде вертикальных линий вдоль оси частот в точках ₀, 2₀, 3₀, и т.д. Высота каждой из этих спектральных линий пропорциональна амплитуде данной частотной составляющей. Обычно частотные составляющие спектра являются комплексными числами, поэтому для представления сложной периодической функции необходимо иметь два частотных спектра – спектр амплитуд (рис 1.4.1а) и спектр фаз (рис. 1.4.1б). Часто эти составляющие являются только действительными или только мнимыми, и данный сигнал можно представить одним спектром амплитуд, так как его фазовый спектр постоянен и имеет составляющие равные 0 или 90.

Спектры периодических несинусоидальных сигналов самой различной формы, но с одинаковым T содержат один и те же гармонические составляющие (основную и кратные ей высшие гармоники), однако амплитуды их различны для различных сигналов. Если построить аналогичные спектры модулей комплексных амплитуд F_k ряда Фурье в комплексной форме, то все спектральные линии будут вдвое короче (F_k = A_k/2), кроме линии, изображающей постоянную составляющую.

Дискретный спектр периодического сигнала, определяемый с помощью специальных средств измерения – анализаторов гармоник, характеризуется совокупностью важных информативных параметров сигнала – значениями амплитуд и фаз отдельных гармоник, полосой частот и т.д.

Рис. 1.4.1. Спектр амплитуд (а) и спектр фаз (б)

Непериодический сигнал x(t) можно представить в пределе как периодический с периодом T. На основе таких представлений получают прямое преобразование Фурье, которое связывает непериодический сигнал x(t) с ее спектральной плотностью S(j)

(1.4.1)

и обратное преобразование Фурье

(1.4.2)

При увеличении T периодический последовательности импульсов разности частот соседних частотных составляющих становятся ничтожно малыми, равными d и дискретный спектр превращается в непрерывную функцию S(j), т.е. в непрерывный спектр.

Спектральная плотность сигнала S(j) является комплексной величиной:

S(j)=A()+jB(), (1.4.3)

где

Модуль и фаза спектральной плотности определяются по формулам

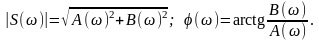(1.4.4)

Периодический сигнал f(t) описывается рядом Фурье и имеет дискретный (линейчатый спектр), изменяющийся в диапазоне частот от 0 до +, а непериодический сигнал x(t) описывается интегралом Фурье и имеет непрерывный (сплошной) спектр, изменяющийся в диапазоне частот от - до +.

Теоретически для большинства периодических сигналов спектр неограничен, т.е. для передачи такого сигнала по каналу канал должен иметь бесконечно большую полосу пропускания. Практически же реальные каналы передачи информации имеют ограниченную полосу пропускания, поэтому форма сигналов при передаче по каналу изменяется даже в отсутствии в этой полосе амплитудных и фазовых искажений. В идеальном случае для передачи сигнала без искажений необходимо передавать все бесконечное число гармоник. На практике приходится передавать не весь спектр импульсного сигнала, а только его часть, ограничиваясь одним, двумя или тремя лепестками спектра. Чем уже полоса частот сигнала, тем заметнее искажение его формы.

Ширина спектра сигнала – это частота самой высокой гармоники в спектре сигнала. За практическую ширину спектра принимают диапазон частот, в пределах которого находится наиболее существенная часть спектра сигнала.

Например, для периодической последовательности однополярных прямоугольных импульсов длительностью  и скважностью Q = 2 ряд Фурье имеет вид

(1.4.5)

где

Спектр состоит из постоянной составляющей и большого числа гармоник, амплитуды которых A₁, A₂, A₃ и т.д. постепенно уменьшаются с ростом частоты (рис.1.4.2). Частота первой гармоники всегда равна частоте следования импульсов. Амплитуда шестой гармоники равна 0 (так как аргумент синуса ). Далее амплитуды гармоник начнут возрастать, а амплитуда 12-й гармоники опять обратиться в ноль. Частоты гармоник, амплитуды которых обращаются в ноль, кратны величине обратной длительности импульса: 1/, 2/, 3/, 4/ и т.д.

Если для передачи такой серии импульсов выделяется полоса частот, равная F_c = 1/ = 1/2010^-3 = 50 Гц, то передача будет осуществляться в нашем случае пятью гармониками (от f₁ = 8,3 Гц до f₅ = 41,64Гц). При увеличении частоты импульсов втрое (при той же длительности ) уравнение (1.4.4) будет иметь вид

(1.4.6)

Амплитуды постоянной составляющей и первой гармоники увеличились (первый лепесток спектра содержит всего одну гармонику), амплитуда второй гармоники (f₂ = 50 Гц) равна нулю. Если передача будет происходить по-прежнему в полосе частот F_c = 50 Гц, то будут переданы только постоянная составляющая и первая гармоника. Однако, несмотря на разное количество передаваемых гармоник, воспроизведение формы импульса в обоих случаях будет почти одинаковым.

А_k

0 ₀2₀4₀6₀8₀ 10₀12₀

Рис. 1.4.2. Спектр периодической последовательности

прямоугольных импульсов

Практически ширина спектра последовательности прямоугольных импульсов выбирается из соотношения F_c = /.

При  = 1 обеспечивается передача основной части энергии сигнала, которая складывается из суммы энергии постоянной составляющей и всех гармоник.

На практике  берется не более 2. В полосе частот F_c = 1/ сосредоточено более 90 % всей энергии сигнала и достаточно точно передается амплитуда прямоугольных импульсов. Третья гармоника добавляет еще 5% энергии, а передача 5-й гармоники обеспечивает 96% энергии сигнала. Ясно, что дальнейшее расширение полосы частот не целесообразно.

Увеличение  приводит не только к более точному воспроизведению формы импульса, но и к значительному расширению полосы частот, что обычно нерационально.

Условием передачи сообщений по каналу без искажения является выполнение условия F_c  F_k, т.е. полоса частот, занимаемая полезным сигналом, не должна превышать диапазона частот канала.