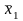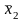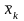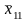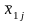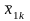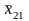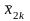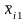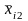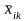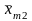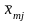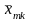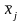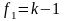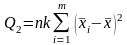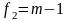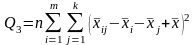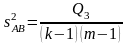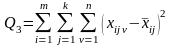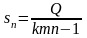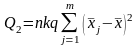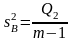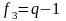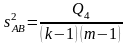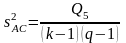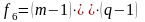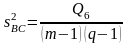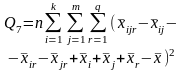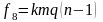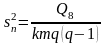4.2. Пассивные эксперименты

При пассивном эксперименте исследователь не имеет возможности воздействовать на изучаемый объект, поэто­му задача планирования эксперимента сводится к опти­мальной организации пассивного сбора информации и включает в себя такие вопросы, как выбор интервалов времени между моментами измерения, задание числа вы­полняемых измерений, выбор метода обработки экспери­ментальных данных и т.д.

Целью пассивного эксперимента часто является постро­ение математической модели объек­та. В зависимости от того, какая математическая модель является подходящей для описания того или иного объекта, последние разделя­ются на хорошо (детерминирован­ные) и плохо (диффузные) органи­зованные объекты. В хорошо орга­низованных объектах можно выде­лить определенные процессы, которые зави­сят от небольшого числа перемен­ных и которые поддаются изучению. Взаи­мосвязи входных и выходных пара­метров объекта в этом случае устанавливаются в виде де­терминированных функций.

В большинстве случаев экспериментатору приходится иметь дело с плохо организованными объектами, когда де­терминированные модели и методы становятся непригод­ными. В таких случаях необходимо использовать статисти­ческие модели и методы, представляющие собой логически обоснованные формализованные методы эксперименталь­ного исследования, когда экспериментатор сознательно от­казывается от детального изучения механизма всех процес­сов и явлений, протекающих в объекте.

При пассивном эксперименте исследователь имеет воз­можность получить путем измерений в различные дискретные моменты времени значения входных параметров x_j объекта и соответствующие им значения выходного пара­метра у. Как отмечалось выше, наличие случайных возму­щающих воздействий делает зависимость выходного па­раметра от входных неоднозначной.

Рассмотрим однофакторный эксперимент, при котором выполнено п пар измерений единственного входного пара­метра х и соответствующих значений выходного парамет­ра у. Результаты измерений изображены графически в виде точек на рис. 4.2.1. Учитывая случайный характер полученных экспериментальных данных, искомую аналити­ческую зависимость у от х можно рассматривать только как зависимость математического ожидания у от значения х. Такая зависимость называется регрессионной, а соот­ветствующая линия на графике (линия АВ) называется линией регрессии.

Целью эксперимента в данном случае является постро­ение регрессионной модели, представляющей собой приб­лиженную оценку истинной регрессионной зависимости. Важным вопросом является выбор вида регрессионной мо­дели, т.е. выбор вида функции, аппроксимирующей экспе­риментальные данные.

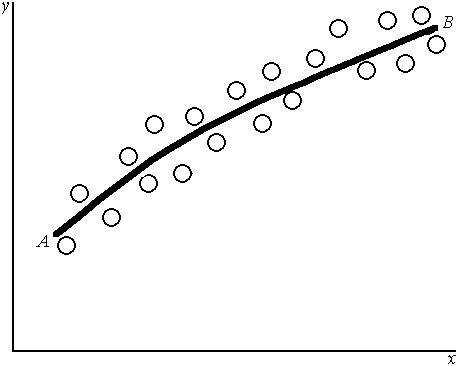
Рис. 4.2.1. График зависимости у от х

4.3. Дисперсионный анализ

Дисперсионный анализ предназначен для выявления степени влияния различных факторов на выходные характеристики при­боров, процессов и т.д.

Обычно принимают предположение о нормальном законе рас­пределения выходной характеристики при фиксированных уровнях факторов. Это распределение вызвано погрешностью измерений, влиянием неконтролируемых условий и т.д., оно проявляется при проведении серии опытов в «одной точке» – при каждом конкретном сочетании уровней факторов. Вторым предположением является однородность дисперсий в «различных точках» – при различных сочетаниях уровней факторов. Для удоб­ства сначала рассмотрим однофакторный дисперсионный анализ, затем двухфакторный и трехфакторный.

В табл. 4.3.1 представлены в общем виде результаты однофакторного дисперсионного анализа. Испытания проводились на k уров­нях фактора А – 1, 2, 3, ..., i, ..., k. На каждом уровне было сделано определенное число опытов – 1, 2, 3, ..., j, ..., n_i и зафиксированы результаты x_{i j}.

Сначала для каждой партии испытаний вычисляют оценки сред­него значения и дисперсии и 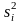по формулам:

(4.3.1)

Затем проверяют однородность ряда дисперсий 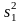, , ..., , ..., по критерию Фишера. После подтверждения гипотезы об однородности этих дисперсий находят оценку общего среднего:

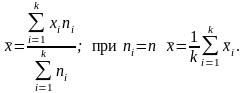(4.3.2)

Таблица 4.3.1

Результаты однофакторного дисперсионного анализа

№ уровня фактора А (партии испытаний)	Результат испытаний	Число опытов n партии	Среднее значение партии	Дисперсия партии
1	x11, x12, …, xij, …, x1n1	n1
2	X21, x22, …, xij, …, x2n1	n2
…	…	…	…	…
i	xi1, xi2, …, xij, …, xin1	ni
…	…	…	…	…
k	xk1, xk2, …, xk j, …, xk n1	nk

Далее вычисляют следующие величины:

– дисперсию 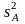, характеризующую рассеивание по факторам, т.е. изменение величины Х (его среднего значения) при изменений уровня фактора А:

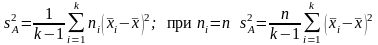(4.3.3)

(число степеней свободы f = k – 1);

– дисперсию 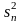(остаточную), характеризующую рассеивание внут­ри партий:

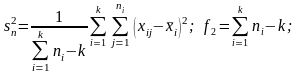(4.3.4)

для n_i = n

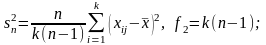(4.3.5)

– полную (общую) дисперсию s², отражающую общее рассеяние как внутри партий, так и за счет изменения уровня фактора:

(4.3.6)

для n_i = n

(4.4.7)

Для выяснения вопроса о том, сказывается ли влияние фактора А, или это влияние несущественно по сравнению с разбросом внут­ри партии, проверяют однородность дисперси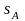й и при помощи критерия Фишера.

Если отношение 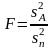окажется меньше табличного значе­ния , найденного для числа степеней свободы f₁ и f₂ и уровня значимости , то влияние фактора несущественно, и все полученные результаты испытаний принадлежат одной генеральной совокуп­ности, распределенной нормально с параметрами ² и а. Их точеч­ные оценки равны соответственно и , а интервальные

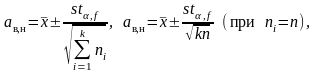(4.3.8)

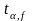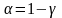где – коэффициент Стьюдента; он находится по таблице для коэффициентов Стьюдента для уровня значимости и степеней свободы. При этом

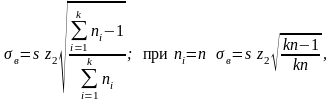(4.3.9)

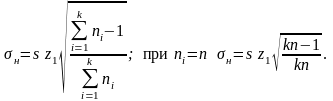(4.3.10)

Значения z₁ и z₂ находят по таблице «Значения z₁ и z₂ для границ доверительного интервала» по уровню  = 1- и .

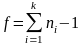Если же справедливо соотношение

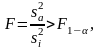(4.3.11)

то влияние фактора существенно. Считается, что есть К нормально распределенных совокупностей, каждая из которых имеет дисперсию ² с разными средними значениями _i. Точечной оценкой ² является s_n, а оценкой средних _i – выборочные средние . Довери­тельные интервалы для _i и  имеют вид:

(4.3.12)

(4.3.13)

(4.3.14)

В формулах (4.3.12) ÷ (4.3.14) .

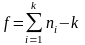Оценку дисперсии средних значений, вызванную влиянием ис­следуемого фактора, производят по формуле

(4.3.15)

Пример 4.3.1. Результаты испытаний при раз­личных уровнях фактора приведены в следующей таблице:

№ партии
1	40,32	0,202
2	41,22	0,196
3	40,31	0,047
4	40,60	0,219
5	40,00	0,065
6	40,73	0,201
7	40,54	0,466
8	40,17	0,076
9	40,26	0,267
10	40,05	0,534
11	40,38	0,149
12	39,93	0,494
13	40,84	0,184
14	40,14	0,426
15	40,60	0,156
Сумма	606,09	3,682

В каждой партии проведено по 20 опы­тов. Проверку однородности дисперсий про­изводят по формуле:

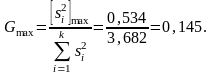
По таблице «Значения G_0,01 (верхняя граница) и G_0,05 (нижняя граница) (Критерий Кохрена) для различных количеств (k)и объемов (n) выборки» для f = п–1 = 20–1 = 19 и k = 15 находим G_0,0l = 0,156 и G_0,05 = 0,139. Значит, подтверждается гипотеза об однород­ности дисперсий для разных партий опытов.

Оценку генерального среднего произво­дят по формуле (4.3.2):

Затем рассчитываем дисперсии , и по формулам (4.3.3), (4.3.5) и (4.3.7):

.

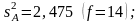
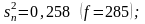
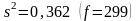Отношение дисперсий F равно:

.

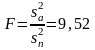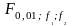Найденное по таблице «Значения (верхние значения) и (нижние значения) для различных степеней свободы f₁ и f₂» значение F_0,99 для числа степеней свободы f₁ = 14 и f₂ = 285 при  = 0,01 составляет 2,15. Так как F > F_0,99, то влияние фактора А на дисперсию весьма существенно.

В завершении определяем генеральную дисперсию средних значений по фор­муле (4.3.15):

В двухфакторном и трехфакторном дисперсионном анализе для удобства вычислений считаем, что для каждой комбинации факторов используется одинаковое число испытаний п. Предположим, что исследуемая величина X в партиях распределена нормально и дисперсии для различных партий опытов однородны. Каждое из этих предположений подлежит проверке по экспериментальным данным перед проведением непосредственно дисперсионного анализа.

Результаты испытаний для двухфакторного анализа приведены в табл. 4.3.2. Один из факторов А имеет k уровней, другой B – m. При каждой комбинации уровней проводится п опытов. Сначала рассчитывают средние значения случайной величины X для каж­дой партии опытов:

Таблица 4.3.2

Результаты испытаний при двухфакторном анализе

Номер уровня фактора B	Номер уровня фактора А
	1	2		…			j		…		k
	Номер испытания в партии
	1, 2, …, , …, n		1, 2, …, , …, n		…	1, 2, …, , …, n		…		1, 2, …, , …, n
1	x111, x112 ,…, x11, …, x11n		x121, x122 ,…, x12, …, x12n		…	x1j1, x1j2 ,…, x1 j , …, x1 j n		…		x1k1, x1 k 2 ,…, x1k, …, x1 k n
2	x211, x212 ,…, x21, …, x21n		x221, x222 ,…, x22, …, x22n		…	x2j1, x2j2 ,…, x2 j , …, x2 j n		…		x2k1, x2k2 ,…, x2 k, …, x2 kn
…	………………		………………		…	………………		…		………………
i	xi11, xi12 ,…, xi1, …, xi1n		xi21, xi22 ,…, xi2, …, xi2n		…	xij1, xij2 ,…, xi j , …, xi j n		…		xi k 1, xi k 2 ,…, xi k , …, xi k n
…	………………		………………		…	………………		…		………………
m	xm11, xm12,…, xm1, …, xm1n		xm21, xm22, …, xm2, …, xm2n		…	xm j 1, xmj2,…, xm j , …, xmj n		…		xmk1, xmk2,…, xmk, …, xmkn

(4.3.16)

затем средние значения по графам 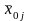(по фактору B) и по строчкам (по фактору А):

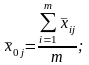(4.3.17)

(4.3.18)

и среднее значение наблюдений : или

(4.3.19)

Результаты этих расчетов приведены в табл. 4.3.3. В соответствии с этой таблицей ведутся вычисления средних значений . Далее вы­числения ведутся с помощью табл. 4.3.4.

Таблица 4.3.3

Средние значения при двухфакторном анализе

Номер строки (уровня фактора В )	Номер столбца (уровня фактора А)						Среднее по строкам
	1	2	…	j	…	k
1			…		…
2			...		...
…	…	…	…	…	…	…		…
i			…		…
…	…	…	…	…	…	…		…
т			...		…
Среднее по столбцам			…		...

После этого с помощью критерия F проверяют гипотезу об от­сутствии взаимодействия между исследуемыми факторами. Для это­го вычисляют дисперсионное отношение

(4.3.20)

и сопоставляют с табличным значением Р_1- (таблица «Значения (верхние значения) и (нижние значения) для различных степеней свободы f₁ и f₂»), найденным для уровня значимости  и числа степеней свободы 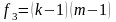и (принимая в таблице f₁ = f₃ и f₂ = f₄). Если справедливо неравенство F > F_1-, то ги­потеза о независимости факторов А и B отвергается и дальше нельзя использовать обычные методы дисперсионного анализа. Если же F  F_1-, то гипотеза об отсутствии взаимодействия подтверждается.

Таблица 4.3.4

Вычисление дисперсии

Компонента дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия
Между средними по графам
Между средними по строкам
При взаимодействии между факторами
Внутри партии (остаточная)
Полная (общая) дисперсия

Затем проверяют значимость влияния обоих факторов на иссле­дуемую величину X. Для этого предварительно объединяют оцен­ки дисперсий и в общую оценку

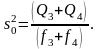(4.3.21)

Далее вычисляют дисперсионные отношения

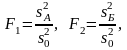(4.3.22)

которые сопоставляют с табличными значениями . Факторы оказывают значимое влияние, если

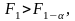(4.3.23)

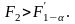_. (4.3.24)

Значение находят по таблице «Значения (верхние значения) и (нижние значения) для различных степеней свободы f₁ и f₂» для числа степеней свободы и 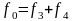, а – для числа степеней свободы и .

Если влияние обоих факторов значимо, то мы имеем дело с km нормально распределенными генеральными совокупностями с об­щей дисперсией ² и разными значениями a_{i j}, оценками которых служат выборочная дисперсия 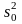и выборочные средние для каждой комбинации факторов . Доверительные интервалы указанных параметров определяют по формулам:

(4.3.25)

(4.3.26)

где .

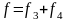При одновременном несоблюдении неравенств (4.3.23) и (4.3.24) подтверждается нулевая гипотеза, т.е. факторы А и B не оказы­вают значимого влияния на величину X. Тогда остается только одна генеральная совокупность результатов испытаний, распределенная по нормальному закону с параметрами ² и а. Оценкой генерального среднего а служит общее выборочное среднее по строкам и столбцам X, а оценкой дисперсии – полная (общая) выборочная дисперсия . В этом случае доверительные интервалы для а и ² вычисляют по формулам:

(4.3.27)

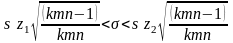(4.3.28)

для 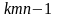степени свободы (т.е. ).

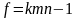При решении практических задач возможны следующие ситуации.

– Выполняются неравенства 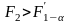. Тогда эффект по столбцам отсутствует (влияние факто­ра А незначительно). Пусть имеется т нормально распределенных совокупностей со средними a_i и одинаковой дисперсией ². Оценками средних а_i являются выборочные средние по строкам , а оценкой дисперсии ² – объединенная выборочная дисперсия

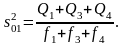(4.3.29)

Границы доверительных интервалов генеральных характеристик для этого случая находят по формулам:

(4.3.30)

, (4.3.31)

где .

– Выполняются неравенства .Тогда эффект по строкам отсутствует (фактор B влияет незначи­тельно). Имеется k нормально распределенных генеральных сово­купностей с общей дисперсией ² и разными средними а_j. Оценками средних а_j служат выборочные средние по столбцам а оценкой дисперсии ² – объединенная выборочная дисперсия

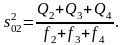(4.3.32)

Доверительные интервалы находят по формулам:

(4.3.33)

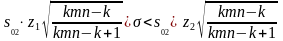(4.3.34)

для степеней свободы (т.е. ).

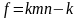В некоторых случаях при каждой комбинации факторов прово­дят только один опыт (т.е. п = 1). Тогда все приведенные выра­жения упрощаются, а 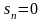. Такой эксперимент используют тогда, когда влияние дестабилизирующих причин в партии опытов несу­щественно и остаточной дисперсией можно пренебречь.

Трехфакторный дисперсионный анализ аналогичен по структуре двухфакторному. Схема анализа для трех факторов А, B, C приве­дена в табл. 4.3.5, которая составлена аналогично табл. 4.3.4.

Проверку нулевых гипотез о незначимости влияния взаимодей­ствия отдельных пар факторов и их общего взаимодействия производят с помощью дисперсионных отношений F₄, F₅, F₆, и F₇, в числителе которых дисперсия для соответствующего взаимодействия ( ,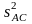 , , 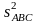), а в знаменателе – остаточ­ная дисперсия . Вычисленные дисперсионные отношения сравни­вают с табличными значениями, найденными для чисел степеней свободы, указанных в табл. 4.3.5.

При принятии нулевых гипотез о взаимодействии факторов дис­персии , , , объединяют в общую оценку

(4.3.35)

Затем с помощью отношений дисперсий , , 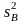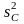к проверяют нулевые гипотезы относительно незначимости влияния каждого фактора. При принятии нулевых гипотез для всех или отдельных факторов возможно дальнейшее объединение дисперсий так, как и при двухфакторном анализе. Доверительные интервалы для диспер­сии и средних значений определяют по формулам, аналогичным приведенным выше.

Таблица 4.3.5

Схема трехфакторного дисперсионного анализа

Ком-понента дисперсии

Сумма квадратов

Число степеней свободы

Дисперсия

1	2	3	4
Между средними фактора А
Между средними фактора B
Между средними фактора C
При взаимодейвии между А и B
При взаимодействии между А и C
При взаимодействии между B и C
При взаимодействии между А, B и C
Внутри партии (остаточная)
Полная дисперсия