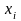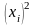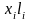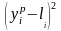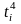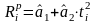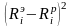- •200106 «Информационно-измерительная техника и технологии»
- •Введение
- •1.2. Сигналы
- •1.3. Преобразование измерительных сигналов
- •1.4. Спектр периодических сигналов
- •1.5. Модуляция
- •1.5.1. Амплитудная модуляция
- •1.5.2. Частотная модуляция
- •1.5.3. Фазовая модуляция
- •1.5.4. Двукратные виды модуляции
- •1.6. Квантование
- •1.6.1. Квантование по уровню
- •1.6.2. Квантование по времени
- •1.6.3. Квантование по уровню и времени
- •1.7. Кодирование
- •1.7.1. Цифровые коды
- •1.7.2. Помехи
- •1.8. Модель канала
- •Раздел 2 измерительные каналы и их разделение
- •2.1. Канал связи и его характеристики
- •2.2. Согласование канала с источником информации
- •2.3. Линии связи для передачи измерительной информации
- •2.4. Структуры линий связи
- •2.5. Многоканальные системы для передачи измерительной информации
- •2.6. Погрешность систем с частотным разделением каналов
- •2.7. Погрешности систем с временным разделением каналов
- •Раздел 3 принципы обработки данных
- •3.1. Виды погрешностей
- •3.2. Обработка результатов измерений. Оценки измеряемой величины
- •3.3. Обработка результатов прямых равноточных измерений
- •3.4. Обработка результатов косвенных измерений
- •3.5. Обработка результатов совместных измерений
- •3.6. Обработка результатов неравноточных измерений
- •3.7. Проверка статистических гипотез
- •3.7.1. Проверка соответствия гипотезы и экспериментальных данных
- •3.7.2. Исключение резко отклоняющихся значений
- •3.8. Построение эмпирических распределений
- •3.9. Критерии согласия
- •3.9.1. Критерий согласия Пирсона
- •3.9.2. Критерий согласия Колмогорова
- •Раздел 4 планирование многофакторного эксперимента
- •4.1. Задачи планирования эксперимента
- •4.2. Пассивные эксперименты
- •4.3. Дисперсионный анализ
- •4.4. Регрессионный анализ
- •4.5. Активный эксперимент
- •4.6. Полный факторный эксперимент
- •4.7. Дробный факторный эксперимент
- •4.8. Устранение влияния временного дрейфа
- •4.9. Проведение факторного эксперимента и обработка его результатов
- •4.10. Оптимизация
- •4.11. Рандомизация
- •Раздел 5 введение в алгоритмическую теорию измерений
- •5.1. Вводные замечания
- •5.2. Развитие понятий числа и измерения величин
- •5.3. Теория шкал и алгоритмические измерения
- •5.4. Алгоритмы измерения в номинальной шкале, аддитивной и порядка
- •5.5. Моделирование цифровых алгоритмических измерений
- •5.6. Эквивалентность между фильтрацией и алгоритмическим измерением
- •5.7. Моделирование сигналов. Дискретизация
- •5.7.1. Модели дискретизации аналогового сигнала
- •5.7.2. Дискретизация с усреднением
- •5.7.3. Дискретизация сигналов конечной длительности
- •5.8. Цифровое представление информации
- •5.9. Системы счисления с иррациональными основаниями
- •5.9.1. Золотая пропорция
- •5.9.2. Числа Фибоначчи
- •5.9.4. Код золотой p-пропорции
- •5.10. Общий алгоритм метрологического кодирования
- •5.10.1. Алгоритм Стахова
- •5.10.2.Фибоначчиевы алгоритмы цифрового метрологического кодирования
- •Раздел 6 введение в информационную теорию измерений
- •6.1. Основные положения теории информации
- •6.1.1. Энтропия
- •6.1.2. Единицы измерения энтропии
- •6.1.3. Условная энтропия (энтропия помехи)
- •6.1.4. Суммирование нескольких погрешностей
- •6.1.5. Явление «краевой эффект». Приближенность информационных оценок каналов передачи информации
- •6.1.6. Основные положения теории информации для характеристики процесса измерения
- •6.2. Сущность измерения
- •6.2.1. Понятие натурального ряда однородных величин
- •6.2.2. Понятие шкалы реперов измеряемой величины
- •6.2.3. Измерение как сужение интервала неопределенности
- •6.3. Измерительные преобразования, функциональные шкалы, единицы измеряемой величины
- •6.3.1. Функциональная шкала измеряемой величины
- •6.3.2. Понятие единицы измерения
- •6.3.3. Метод построения измерительных устройств
- •6.4. Измерительные преобразования и преобразователи
- •6.5. Энтропийное значение погрешности
- •6.5.1. Математическое определение энтропийного значения погрешности
- •6.5.2. Эффективное значение погрешности
- •6.6. Сравнение энтропийного и среднеквадратического значений погрешности для плавных симметричных одномодальных законов распределения погрешностей
- •6.7. Энтропийное значение погрешности – основной критерий точности приборов и измерений
- •6.8. Определение энтропийного значения погрешности на практике
- •6.9. Суммирование погрешностей измерительных устройств
- •6.10. Статистическое суммирование погрешностей при наличии корреляции
- •6.11. Энтропийное значение результирующей погрешности
- •6.12. Суммирование погрешностей с равномерными законами распределения вероятностей
- •6.13. Суммирование погрешностей при равномерном и нормальном законах распределения составляющих результирующей погрешности
- •6.14. Суммирование погрешностей при произвольной степени корреляции и произвольных законах распределения вероятностей составляющих результирующей погрешности
- •И объемов (n) выборок
- •Интервала
- •Оглавление
3.5. Обработка результатов совместных измерений
При совместных измерениях искомые значения величин находят решением системы уравнений, связывающей эти величины с непосредственно измеряемыми.
Предположим сначала, что искомые значения величин определяются в результате решения системы линейных уравнений:
 (3.5.1)
(3.5.1)
где
 – искомые значения величин;
– искомые значения величин;
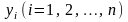 – измеряемые значения величин;
– измеряемые значения величин;
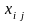 – известные
значения величин.
– известные
значения величин.
Запишем систему уравнений (3.5.1) в виде
 (3.5.2)
(3.5.2)
Предположим,
что уравнения (3.5.2) являются точными, но
значения
 получены
с погрешностями. Пусть результаты
измерений величин
равны
получены
с погрешностями. Пусть результаты
измерений величин
равны  :
:
 (3.5.3)
(3.5.3)
где – погрешность измерения величины .
Тогда
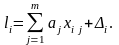 (3.5.4)
(3.5.4)
Очевидно, что при решении системы уравнений (3.5.2) вместо будут использоваться измеренные значения . В этом случае, если число измерений п больше числа неизвестных т (n > m), система уравнений (3.5.2) не имеет решения, т.е. нет такого набора значений , которые удовлетворяли бы всем п уравнениям системы. Поэтому уравнения (3.5.2) называются условными уравнениями.
Относительно погрешности сделаем следующие допущения:
1)
погрешность
является нормально распределенной
случайной величиной с нулевым
математическим ожиданием
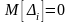 и дисперсией 2,
одинаковой во всех измерениях;
и дисперсией 2,
одинаковой во всех измерениях;
2) погрешности отдельных измерений независимы. Из (3.5.4) следует, что величина будет иметь нормальное распределение с параметрами
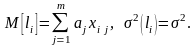 (3.5.5)
(3.5.5)
Запишем плотность распределения величины :
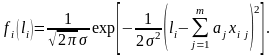 (3.5.6)
(3.5.6)
Тогда функция правдоподобия
 .
(3.5.7)
.
(3.5.7)
Найдем оценки
 из условия максимума функции
правдоподобия. Прологарифмируем (3.5.7):
из условия максимума функции
правдоподобия. Прологарифмируем (3.5.7):
 (3.5.8)
(3.5.8)
Условием максимума функции (3.5.8) является
 (3.5.9)
(3.5.9)
или
 (3.5.10)
(3.5.10)
Таким образом, условие (3.5.9) является требованием метода наименьших квадратов. Следовательно, в данном случае при нормальном распределении случайной погрешности оценки метода максимального правдоподобия и метода наименьших квадратов совпадают.
Для нахождения значений оценок , удовлетворяющих (3.5.9), необходимо добиться равенства нулю всех частных производных от этой функции по . Отсюда получим:
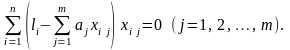 (3.5.11)
(3.5.11)
Система уравнений (3.5.11) также является линейной относительно величин и называется системой нормальных уравнений. Число нормальных уравнений системы (3.5.11) всегда равно числу неизвестных величин, оценки которых находятся в результате решения этой системы.
Сгруппировав все коэффициенты при неизвестных , получим стандартную запись системы нормальных уравнений:
 (3.5.12)
(3.5.12)
В
(3.5.12) xj
и l
рассматриваются как n-мерные
векторы с компонентами
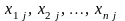 и
и
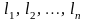 соответственно.
соответственно.
Коэффициенты
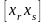 и свободные члены
и свободные члены
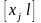 представляют
собой скалярные произведения
соответствующих векторов:
представляют
собой скалярные произведения
соответствующих векторов:
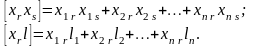 (3.5.13)
(3.5.13)
Тогда искомые оценки величин могут быть вычислены из (3.5.12) методом определителей
 (3.5.14)
(3.5.14)
где
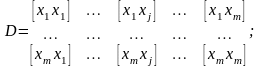

Определитель
 получен
заменой в определителе D
j-го
столбца столбцом свободных членов
системы нормальных уравнений.
получен
заменой в определителе D
j-го
столбца столбцом свободных членов
системы нормальных уравнений.
Полученные оценки являются состоятельными, несмещенными, а для нормального распределения погрешности и эффективными.
Используя те же экспериментальные данные, найдем оценку дисперсии случайной погрешности. Для этого воспользуемся формулой логарифма функции правдоподобия:
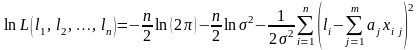 . (3.5.15)
. (3.5.15)
Найдем оценку дисперсии 2, обеспечивающую максимум (3.5.15):
 (3.5.16)
(3.5.16)
Подставив вместо оценки , получим:
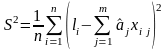 .
(3.5.17)
.
(3.5.17)
Оценка S2 является смещенной, а для устранения этой смещенности необходимо перейти к оценке
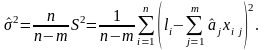 (3.5.18)
(3.5.18)
Оценим погрешности найденных значений величин . Оценки дисперсий значений можно вычислить, пользуясь формулой
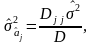 (3.5.19)
(3.5.19)
где
D
– главный
определитель системы нормальных
уравнений;
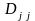 –
алгебраическое дополнение определителя
D,
получаемое путем удаления из определителя
D
j-й
строки и j-го
столбца;
– оценка дисперсии погрешности прямых
измерений.
–
алгебраическое дополнение определителя
D,
получаемое путем удаления из определителя
D
j-й
строки и j-го
столбца;
– оценка дисперсии погрешности прямых
измерений.
Пример 3.5.1. В результате выполнения совместных измерений находятся параметры линейной зависимости
у = а1 + а2х. (3.5.20)
Система нормальных уравнений примет вид:
 (3.5.21)
(3.5.21)
Преобразовав (3.5.20) получим:
 (3.5.22)
(3.5.22)
где
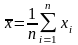 ;
; 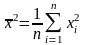 ;
; 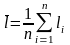 ;
; 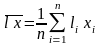 .
.
В результате решения (3.5.21) находим оценки
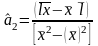 ;
;
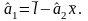 (3.5.23)
(3.5.23)
Аналогично решается задача определения параметров полиноминальных зависимостей более высоких порядков.
Пример 3.5.2.
Определить параметры a
и b
в линейной зависимости
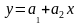 ,
а также случайные погрешности их
измерения (систематические погрешности
отсутствуют) по результатам 10 измерений,
приведенным во 2-м и 3-м столбце табл.
3.5.1:
,
а также случайные погрешности их
измерения (систематические погрешности
отсутствуют) по результатам 10 измерений,
приведенным во 2-м и 3-м столбце табл.
3.5.1:
Таблица 3.5.1
№ измерения |
|
|
|
|
|
|
|
1 |
0 |
2,2 |
0 |
0 |
1,949 |
-0,251 |
0,063 |
2 |
0,5 |
2,4 |
0,25 |
1,2 |
2,48175 |
0,08175 |
0,00668 |
3 |
1,0 |
3,0 |
1,0 |
3,0 |
3,0145 |
0,0145 |
0,00021 |
4 |
1,5 |
3,2 |
2,25 |
4,8 |
3,54725 |
0,34725 |
0,1206 |
5 |
2,0 |
3,9 |
4,0 |
7,8 |
4,08 |
0,18 |
0,0324 |
6 |
2,5 |
4,8 |
6,25 |
12,0 |
4,61275 |
-0,18725 |
0,035 |
7 |
3,0 |
4,9 |
9,0 |
14,7 |
5,1455 |
0,2455 |
0,0603 |
8 |
4,0 |
6,2 |
16,0 |
24,8 |
6,211 |
0,011 |
0,00012 |
9 |
5,0 |
7,3 |
25,0 |
36,5 |
7,2765 |
-0,0235 |
0,00055 |
10 |
6,0 |
8,1 |
36,0 |
48,6 |
8,342 |
0,242 |
0,0585 |
∑ |
25,5 |
46,0 |
99,75 |
153,4 |
|
|
0,37736 |
Решение. На основании примера 3.5.1. и приведенных данных обработки экспериментальных результатов запишем нормальные уравнения (3.5.22):

Используя (3.5.23), (3.5.18) и результаты вычисления в таблице 3.5.1, получаем искомые оценки
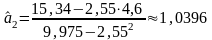 ;
;  ,
,
а также оценки дисперсии и среднего квадратического отклонения измерения:
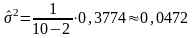 ;
;  .
.
В
соответствии с (3.5.19) погрешности найденных
значений величин
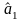 и
и
 будут
равны:
будут
равны:
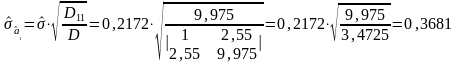 ;
;
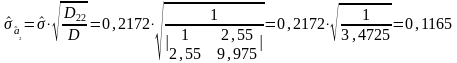 .
.
Пример
3.5.3. Зависимость
электрического сопротивления
композиционного материала от температуры
выражается формулой
 .
Для определения коэффициента
было проведено 13 равноточных измерений
сопротивления при различной температуре
(табл. 3.5.2). Используя метод наименьших
квадратов, вычислить оценку коэффициента
.
.
Для определения коэффициента
было проведено 13 равноточных измерений
сопротивления при различной температуре
(табл. 3.5.2). Используя метод наименьших
квадратов, вычислить оценку коэффициента
.
Таблица 3.5.2
i |
ti, C |
Ri, Ом |
|
|
|
|
|
|
1 |
10 |
128 |
100 |
12800 |
10000 |
130,092 |
-2,09201 |
4,376513 |
2 |
12 |
140 |
144 |
20160 |
20736 |
143,2889 |
-3,28888 |
10,81672 |
3 |
15 |
170 |
225 |
38250 |
50625 |
167,5831 |
2,41689 |
5,841355 |
4 |
18 |
190 |
324 |
61560 |
104976 |
197,2761 |
-7,27606 |
52,94106 |
5 |
20 |
230 |
400 |
92000 |
160000 |
220,0706 |
9,929352 |
98,59202 |
6 |
25 |
290 |
625 |
181250 |
390625 |
287,5546 |
2,445374 |
5,979854 |
7 |
30 |
365 |
900 |
328500 |
810000 |
370,035 |
-5,03504 |
25,35166 |
8 |
35 |
475 |
1225 |
581875 |
1500625 |
467,5119 |
7,488101 |
56,07165 |
9 |
40 |
570 |
1600 |
912000 |
2560000 |
579,9852 |
-9,9852 |
99,70412 |
10 |
45 |
710 |
2025 |
1437750 |
4100625 |
707,4549 |
2,54507 |
6,47738 |
11 |
50 |
855 |
2500 |
2137500 |
6250000 |
849,9211 |
5,078895 |
25,79517 |
12 |
55 |
1010 |
3025 |
3055250 |
9150625 |
1007,384 |
2,616281 |
6,844925 |
13 |
60 |
1175 |
3600 |
4230000 |
12960000 |
1179,843 |
-4,84277 |
23,45245 |
∑ |
|
6308 |
16693 |
13088895 |
38068837 |
|
|
422,2449 |
Решение. Представим зависимость сопротивления от температуры в виде:
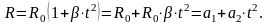
Измеренные значения
сопротивления
 приведены во 2-м и 3-м столбцах таблицы.
приведены во 2-м и 3-м столбцах таблицы.
Система нормальных уравнений имеет вид:

Подставив в эту систему данные из последней строки табл. 3.5.2, получаем систему нормальных уравнений с числовыми коэффициентами:
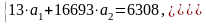
Вычислив
определители
 ,
получим
,
получим
 ;
;
 .
.
Используя (3.5.18), (3.5.19) и результаты обработки данных, приведенные в таблице 3.5.2, получаем среднюю квадратическую погрешность результатов измерения параметров и :
 ;
;  ;
;

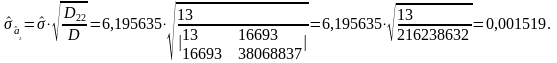
Так как было введено
обозначение
 ,
то
,
то
 .
Средняя квадратическая погрешность
температурного коэффициента
может быть определена с помощью формулы
(3.4.8) для косвенных измерений:
.
Средняя квадратическая погрешность
температурного коэффициента
может быть определена с помощью формулы
(3.4.8) для косвенных измерений:
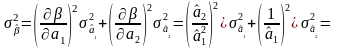
 .
.
Отсюда
 .
.
Таким образом результат измерения можем записать:
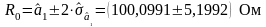 ;
;
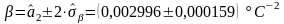 .
.